BRIFT： 一种基于二值描述符的多模态图像匹配方法

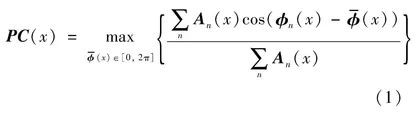
摘要：       针对使用辐射变化不敏感特征变换（RIFT）在最大索引图（MIM）上计算特征描述符、 进行特征匹配耗费时间长的问题， 提出了基于RIFT的二值描述符算法（BRIFT）。 首先计算图像的相位一致性并得到MIM， 然后在MIM上通过快速算法计算特征描述符并将其二值化， 最后利用Hamming距离作为距离测度进行匹配。 将存在多种几何畸变和辐射度变化的异源遥感图像作为测试数据， 将BRIFT算法分别与SIFT， BRISK， BRIEF， RIFT等方法进行对比， 结果表明， 在略微损失匹配精度的情况下， 所提BRIFT算法能节省约80%～90%的特征描述符计算时间， 节省约50%的特征匹配时间， 实现异源遥感图像的快速鲁棒匹配。

关键词：      图像匹配；  特征匹配；  相位一致性；  最大索引图；  二值描述符

中图分类号：       TJ760；  TP751    文章编号：      1673-5048（2023）04-0115-08

文献标识码：     A    DOI：  10.12132/ISSN.1673-5048.2022.0263

0引言

图像匹配是将由不同传感器、 在不同时间拍摄的图像在空间位置上进行对齐配准的过程。 由于不同传感器成像机理不同， 成像时间、 视角也不同， 因此图像配准可以提供互补的信息， 被广泛应用于如地物勘测、 图像融合、 图像检索、 变化检测、 计算机视觉等方面。 近年来， 随着红外、 激光、 SAR等成像技术的快速发展， 产生的海量数据对图像的快速鲁棒配准提出了更高要求。 此外， 由于异源图像通常由不同传感器在不同时间获得， 因此图像之间存在较大的非线性辐射度差异及时相差异， 导致图像匹配性能较差。

图像匹配方法通常分为三类： 基于灰度的图像匹配方法、 基于特征的图像匹配方法和基于表示的图像匹配方法。 基于灰度的图像匹配方法直接利用图像的灰度值， 即根据一定的相似性度量方法， 计算模板窗内两幅图像灰度值的相似度， 从而将相似度最大的位置作为匹配位置。 常用的相似性度量方法有平方差（Sum of Squared Difference，  SSD）［1］、 互相关（Cross Correlation，  CC）、 归一化互相关（Normalized Cross Correlation，  NCC）［2］和互信息（Mutual Information，  MI）［3］。 这类方法通常无法用来匹配含有非线性辐射度变化的多模态图像。 基于表示的图像匹配方法［4］首先利用机器学习等方法获得对待匹配区域的解释表示， 然后借助语义网络等方法， 实现图像的配准， 在缺少训练样本时或者实时性要求比较高时， 无法实现异源图像的快速鲁棒配准。

基于特征的图像匹配方法首先在待匹配图像之间寻找具有显著特征的点， 如角点、 线交叉点、 边缘点等， 然后利用特征点及其周围的像素形成特征点的特征表示， 最后再根据一定的搜索策略在特征表示之间寻找具有匹配关系的特征点。 由于考虑了特征点周围的统计信息， 并对特征向量进行了归一化， 因此能抵抗旋转、 光照和尺度变化。 基于特征的图像匹配方法中， 尺度不变特征变换（Scale Invariant Feature Transform，  SIFT）［5-7］最早被提出。 SIFT在高斯差分尺度空间（Laplacian of Gaussian，  LoG）中检测角点， 并利用特征点周围的梯度信息构造特征点的特征描述， 因此对一般的仿射变换都具有不变性， 但是受限于计算效率问题。  加速鲁棒特征（Speed-up Robust Features，  SURF）［8］和PCA-SIFT［9］以损失一定匹配精度为代价， 通过降低特征描述符的长度以实现对SIFT算法的加速。  BRIEF（Binary Robust Independent Elementary Features）［10］和ORB特征［11］也是以损失匹配精度为代价， 利用二值特征描述符减少描述符的占用空间并利用二值描述符的快速匹配策略加速匹配。  BRISK（Binary Robust Invariant Scalable Keypoints）［12］算法利用环形采样模式以解决BRIEF［10］算法存在的不能抵抗旋转差异的问题。  SAR-SIFT［13］利用比率梯度代替差分梯度， 从而增强SAR图像匹配的鲁棒性。 近年来， 国内一些学者提出了多种新的多模图像匹配方法， LSS［1］利用局部自相似性即图像块与周围区域的相关系数进行匹配， 可以实现具有相同区域模式图像的匹配。 CFOG［14］利用图像在多个方向上的变化率（多方向梯度）构造每个像素的特征表示， 可以实现多模图像匹配。 HOPC［15］和RIFT（Radiation-Variation Insensitive Feature Transform）［16］利用图像相位一致性提取图像的特征点， 可以实现具有非线性灰度变化的多模图像的鲁棒匹配， 但是对图像之间的旋转差异适应性差且运算量大。 HAPCG［17］利用各向异性加权力矩和绝对相位一致性方向直方图进行多模图像匹配， 提高了多模图像匹配的精度。

总而言之， 基于特征的图像匹配方法利用了特征点及其周围像素的统计信息， 在存在光照、 旋转和尺度差异的图像匹配上效果较好。 由于多模图像之间存在非常大的几何、 灰度、 时相差异， 因此使用SIFT等依赖梯度的方法并不能取得令人满意的效果。 较新的方法如HOPC［15］和RIFT［16］等不依赖于图像的梯度信息， 对具有非线性灰度差异的多模图像匹配效果较好， 但存在计算效率不高、 不利于工程应用的问题。 本文提出的基于RIFT［16］的二值描述符算法（Binary Descriptor for RIFT，  BRIFT）利用相位一致性和RIFT［16］算法中的最大索引图（Maximum Index Map，  MIM）， 结合BRIEF［10］算法中将特征描述符二值化的思想， 对RIFT算法计算效率不高的问题进行了改进， 将RIFT算法运算速度提高了一个数量级。 所提BRIFT算法首先利用快速算法在MIM上计算二值特征描述符， 然后利用Hamming距离作为测度进行特征匹配， 最后利用随机采样一致性算法［18］估算两幅图像之间的仿射变换矩阵， 从而剔除误匹配点， 实现多模图像的快速鲁棒匹配。

1相位一致性及特征描述符的快速计算

1.1相位一致性

使用相位一致性提取特征的思路来源于信号的Fourier分解， 考虑如图1所示的方波信号和三角波信号及其谐波分量。 在方波信号的阶跃位置和三角波信号的波峰波谷位置， 其谐波分量有近似一致的相位， 如谐波分量在方波阶跃位置相位均为0， 在三角波波峰波谷的位置相位均为0或者π， 而方波的阶跃位置和三角波的波峰波谷一般是信号中具有明显特征的位置。

相位一致性通过式（1）计算：

式中： ω0（x， y）为一频率扩展加权函数， 作用是当（x， y）处信号的频率分布较窄时对该位置进行惩罚， 即信号所包含的频率范围越宽， 其对相位一致性的贡献越大；  Aso（x， y）表示将图像I与尺度为s、 方向为o的log-Gabor正交滤波器Leven和Lodd卷积的幅度响应， 即

［Eso（x， y）， Oso（x， y）］=［I（x， y）*Leven（x， y， s， o）， I（x， y）*Lodd（x， y， s， o）］

log-Gabor滤波器定义在频域［19］， 其IFFT的实部对应滤波器的偶对称部分Leven， 虚部对应滤波器的奇对称部分Lodd；  ·」是为了防止所包含的部分为负数， 即当所包含的部分为负数时将其置为0；  ε为一个避免分母为零的小的常数；  T为一噪声阈值， 其作用是提高对含有噪声信号的特征检测能力；  ΔΦso为相位偏差函数， 其定义如下：

相比于式（1）中的相位偏差， 该定义下的相位偏差可以提供更好的特征定位能力。

根据式（2）， 为计算相位一致性， 需要将图像与多个尺度和方向上的log-Gabor滤波器进行卷积， 对于所有方向θo， 相位一致性的协方差矩阵为

根据矩分析理论， 最小矩mψ对应于图像中的角特征， 最大矩Mψ对应图像中边缘线特征。 由于最大矩Mψ图中非零元素更多， 因此可以检测到更鲁棒的特征。 本算法通过在最大矩图中执行FAST［20］检测得到特征点的位置。

1.2最大索引图及特征描述符快速计算方法

Li等［16］在RIFT算法中指出， 由于相位一致性图中大部分像素为0， 在相位一致性图上构造的特征描述符不足以完成多模图像的鲁棒匹配， 因此RIFT在最大索引图（MIM）上构造特征描述符。 最大索引图构造方式如图2所示，

其中：  A1～A6为将原图像在各尺度滤波结果相加， 得到在不同相角处的相位一致性； MIM为相位一致性最大处所在相角的索引。

在计算相位一致性时， 将图像与Ns个尺度和No个方向上的log-Gabor正交滤波器对进行卷积， 其幅度响应为Aso， 因此在给定方向o上的相位一致性Ao为最大索引图定义为所有No个方向中， 相位一致性最大的Ao所在的方向序号。 考察相位一致性的意义可知， 最大索引图实质上是将相位一致性方向量化到No个方向， 因此MIM（x， y）∈［1， No］。 RIFT算法［16］中通过实验确定使用Ns=4个尺度和No=6个方向以得到最优的结果。 为了与该算法对比， 所提BRIFT算法使用了相同的参数设置。

RIFT算法使用最大索引图构造特征描述符， 即对1.1节中检测到的特征点， 将以特征点为中心的图像区域切分为若干个block， 统计每个block的直方图， 将统计得到的直方图级联为一特征向量形成对特征点的特征描述。 然而， 统计直方图至少需要对每个block内的像素进行遍历， 时间复杂度为O（n）， 当特征点数量比较多时， 该步骤将耗费大量时间。 实际上， 由于MIM（x， y）∈［1， No］， 所以计算直方图可以通过盒式滤波简化为No次查表操作， 时间复杂度降低为O（c）， 具体如图3所示。 首先， 将MIM分解为No个子图， 每个子图仅包含相同的相位一致性方向索引。 其次， 将每个子图与求和滤波器进行卷积， 卷积核的大小与计算直方图的block的大小一致， 其中i表示方向索引。 因此， 卷积结果（查找表）中每个像素的值就表示以该像素为中心， 大小为block的范围内， 含有相同相位一致性方向索引像素的个数。 最后， 当需要计算某个block内的直方图时， 只需要在No个查找表上查找与block中心像素相同位置的元素值， 将这No个结果合在一起， 就构成了该block的直方图表示。 在实验部分， 对于含有5 000个特征点的图像（图像大小为500×500）， BRIFT算法可以节省约90%的计算时间。

2二值特征描述符

使用二值特征描述符的优势在于节省特征描述符的存储空间并加速特征匹配过程。 对于浮点数据类型的描述符， 在描述符长度相同时其占用空间约为二值化特征描述符的4倍。 其次， 浮点类型的特征描述符匹配需要计算浮点向量之间的欧氏距离， 由于现代计算机浮点数据的运算指令周期长于整型数据的运算指令周期， 因此特征匹配耗时更长， 而对于二值化的特征描述符， 特征匹配只需要计算特征描述符之间的Hamming距离， 即只需要将两个特征描述符进行异或操作即可， 可以大大节省特征匹配耗时。

2.1在MIM上应用BRIEF描述符

BRIEF［10］算法改进特征描述符的方式如下， 对于大小为S×S的像素区域p， 定义测试τ为

式中： I（p， x）为图像区域p中在位置x=（u， v）T处的图像灰度值。 通过选择nd个点对（x， y）， 就构成了区域p上的一个二值测试集， nd就是特征描述符的长度， 其BRIEF描述符定义如下：

BRIEF算法中给出了五种测试点对（x， y）的分布， 并指出当点对（x， y）相对于区域中心均服从高斯分布时， 所形成的二值描述符具有最高的识别率。 然而， 将BRIEF算法直接应用于相位一致性图或者最大索引图时， 均未取得期望的结果。 主要原因为： （1）将BRIEF算法应用于相位一致性图时， 由于相位一致性图中大部分像素均为0， 因此在给定的nd次测试下， 其结果也大部分为0， 因此形成的特征描述符可分性不高， 不能实现多模图像的鲁棒匹配；  （2）将BRIEF算法应用于最大索引图时， 由于多模图像之间非线性灰度差异较大， 因此两幅图像在相同测试点对处不一定有相同的相位一致性方向关系；  （3）将BRIEF算法应用于最大索引图时， 由于受到噪声等因素的影响， 单个点处的相位一致性方向可能并不准确， 其位置可能发生偏移， 从而造成该位置处的测试失效， 影响最终的匹配性能。