高超声速滑翔飞行器协同轨迹规划方法

摘 要：  为了满足高超声速滑翔飞行器协同再入的时间和角度需求，考虑过程约束和交班点约束，提出了一种多约束协同再入轨迹规划算法。将时间约束和角度约束分解到纵向和横向两个平面，采用牛顿迭代法规划阻力加速度-能量剖面，得到满足时间和航程约束的纵向轨迹，利用序列二次规划方法搜索倾侧角翻转点，使轨迹终端满足角度约束，通过多次迭代更新，可以得到满足时间和角度约束的三维轨迹。在此基础上，分析了单个飞行器的飞行能力，给出了协同参数的确定方法。数值仿真结果表明，该方法能够在协同打击、协同投递等多种场景中应用，为飞行器规划出具有较高时间和角度精度的三维轨迹，任务适应性强，能够满足更多的约束和协同需求。

关键词：高超声速飞行器；协同再入；轨迹规划；时间协同；方向协同；协同策略

中图分类号：TJ765；V412.4

文献标识码：A

文章编号：1673-5048（2022）05-0001-10

DOI：10.12132/ISSN.1673-5048.2022.0097

0 引  言

高超声速滑翔飞行器是一种由火箭助推至高空或者从卫星发射的高超声速飞行器，该类飞行器通常具有大升阻比的气动特性，飞行马赫数超过5，能够在大气层内进行远距离滑翔［1］。凭借飞行高度高、速度大、射程远、机动能力强等出众的性能特点［2-3］，高超声速滑翔飞行器在远程突防和精确打击等领域有着广泛应用［4］。

近年来，由于防空反导技术快速发展，单枚飞行器的突防能力持续被削弱，为了继续保持高超声速再入滑翔飞行器的作战优势，一些学者提出将集群控制技术应用在高超声速滑翔飞行器上，通过多枚高超声速滑翔飞行器协同飞行，相互配合，共同执行任务，从而扩展高超声速滑翔飞行器的应用领域，增加高超声速滑翔飞行器的突防概率。

集群控制技术中应用较多的是以无人机、巡航导弹为对象的编队控制技术，通过领-从式策略、虚拟刚体策略等控制多枚飞行器协同飞行。但是无人机和巡航导弹的很多协同制导方法都应用了定常匀速假设，且飞行过程中的约束比较少。与其相比，高超声速滑翔飞行器的再入过程是无动力滑翔，速度无法直接控制，而且飞行环境复杂，需要考虑热流密度、动压等过程约束，另外飞行速度较快、分布空域大，弹间通信不便，所以相关编队控制技术无法直接应用在高超声速滑翔飞行器上。为了解决高超声速滑翔飞行器的协同问题，一些学者改变思路，通过协同轨迹规划，根据一定协同策略为每枚高超声速滑翔飞行器规划相应的轨迹，从而可以在轨迹的终端实现某一方面的协同。

对于时间协同的研究中，文献［5］通过对到达时间进行预测，得到协同飞行时间，以此作为终端时间约束，基于Radau伪谱法进行轨迹优化，从而实现时间协同。文献［6］将飞行时间误差加入到罚函数中，提出了一种基于序列凸优化的协同轨迹快速规划算法，提高了协同轨迹求解的可行性与计算速度。文献［7］建立剩余飞行时间和末制导交班点速度的对应关系，运用预测-校正方法，同时满足末端能量和时间约束。文献［8］设计了一种动态参考剖面，通过对攻角剖面和高度-速度剖面的参数进行不断校正，使飞行器轨迹满足时间约束。文献［9］基于双参数牛顿迭代法设计阻力加速度剖面，结合可调边界的航向偏差走廊，生成满足时间约束的参考轨迹。文献［10］基于非线性再入动力学方程推导出高精度的飞行时间解析解，设计了满足时间约束的飞行轨迹。

此外，文献［11］基于神经网络建立航向偏差走廊和飞行时间的关系，使轨迹满足时间约束。文献［12］采用深度Q-学习网络求解飞行器横向机动解析解，实现时间协同再入飞行。文献［13］利用多边界航向偏差走廊调节飞行时间，使多枚飞行器同时到达目标。文献［14］运用模型预测静态规划（MPSP），求解具有硬终端约束的飞行器协同再入控制指令，实现对多个目标的协同打击。与时间协同相比，方向协同的研究文献较少，文献［15］通过序列二次规划方法（SQP）搜索满足接近角约束的地面瞄准点，实现航天器固定角度再入。文献［16］研究了助推滑翔飞行器的弹道特点，采用设置虚拟目标点的方式控制飞行器到达目标的角度。

以上学者大多数只研究了时间协同和方向协同的一种，并未将两种协同方式结合，无法满足饱和打击、协同运输等任务需求。针对该问题，本文在文献［9］和［15］的基础上进行改进，提出一种能够同时满足时间约束和角度约束的协同轨迹规划方法。首先，设计攻角剖面，采用牛顿迭代法设计阻力加速度-能量剖面，得到满足时间、航程等约束的纵向轨迹。然后，采用SQP方法搜索满足角度约束的倾侧角的翻转能量点，从而通过轨迹规划实现单枚飞行器的时间、角度控制。在此基础上，分析单枚飞行器的飞行能力，提出协同时间和协同方向的确定方法，实现多枚飞行器的时间、方向协同轨迹规划。最后，通过仿真证明了本文提出的协同轨迹规划方法的有效性。

1 多飞行器协同再入问题描述

1.1 协同再入问题

1.1.1 协同需求

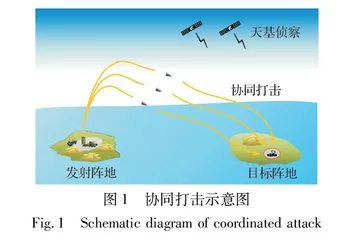
在高超声速滑翔飞行器协同打击、协同投递等典型作战场景中，根据作战任务，多枚飞行器再入飞行存在相应的协同需求。图1为多枚高超声速滑翔飞行器对目标协同打击的场景示意图，图2为多枚高超声速滑翔飞行器协同投递小型飞行器作战的场景示意图。

图1中，多枚高超声速滑翔飞行器从发射阵地发射后，向目标阵地协同飞行，期望同一时刻从不同方向对目标进行协同打击，从而增加突防概率，提高对目标的杀伤效果。图2中，多枚高超声速滑翔飞行器从发射阵地发射后，向目标阵地协同飞行，在不同时间以相同方向到达固定区域进行协同投递，抛撒小型飞行器，使小型飞行器快速集结成编队，对目标进行蜂群作战。

从两个典型场景中可以看出，协同再入飞行常见的协同需求有时间协同和方向协同，时间协同又有同时刻协同和分批次协同两种，方向协同又有相同方向和不同方向两种，而且常常两种协同需求需要同时得到满足。

1.1.2 协同阶段

根据高超声速滑翔飞行器的受力以及飞行环境变化，可以将飞行过程分为主动段、自由飞行段、再入滑翔段和下压段。图3为高超声速滑翔飞行器的弹道示意图，展示其主要飞行阶段。

在高超声速滑翔飞行器的主要飞行阶段中，主动段和自由飞行段作为初始阶段，飞行时间短、机动能力弱，弹道相对固定，难以进行协同规划；下压段作为最后飞向目标的阶段，飞行距离和时间比较短，同样不适合进行协同飞行；而再入滑翔段占据了整个飞行过程80%以上的航程，飞行时间长、机动能力较强，所以适合作为协同飞行的主要阶段。

1.2 飞行器数学模型

1.2.1 动力学模型

高超声速滑翔飞行器的再入飞行环境和动力学模型较为复杂，建模时考虑所有的因素不利于分析其飞行特性。为了简化问题，将影响较小的因素忽略，对飞行器运动过程进行简化，作如下假设：

（1） 将地球看作一个均质球体；

（2） 将飞行器看作是一个质点；

（3） 再入过程中飞行器质量不变；

（4） 忽略外界的干扰。

高超声速滑翔飞行器采用BTT方式转弯，所以侧滑角β=0°，而且再入段无推力作用，在大地坐标系下建立第i枚高超声速滑翔飞行器的三自由度动力学方程：

dridt=Visinθi

dVidt=－Ximi－gsinθi

dθidt=1ViYicosσimi+V2iri－gcosθi

dψidt=1ViYisinσimicosθi+V2iricosθisinψitani

dλidt=－Vicosθisinψiricosi

didt=Vicosθicosψiri （1）

式中：下标i代表第i枚飞行器；λ为飞行器经度；为飞行器纬度；r为飞行器与地心距离；V为飞行器速度；θ为弹道倾角；ψ为航向角；σ为倾侧角；m为飞行器质量；g为重力加速度， g=g0R20r2；

X和Y分别为飞行器所受的阻力和升力：

X=Cx（Ma， α）qSrefY=Cy（Ma， α）qSref

式中：α为气动攻角；Ma为马赫数，是飞行器速度与当地声速的比值；Sref为参考面积；Cx，Cy分别为阻力系数和升力系数，可以通过攻角与马赫数对气动系数插值表二维插值得到；q为动压。

q=12ρV2

式中：ρ=ρ0exp－HHs为大气密度，

Hs=6 700 m， ρ0=1.752 kg/m3， H=r－R0， R0为地球半径。

1.2.2 约束模型

高超声速滑翔飞行器再入飞行过程中，考虑到外界环境、飞行器材质以及飞行任务的影响，飞行器需要满足以下约束。

（1） 过程约束

第i枚飞行器的热流密度、动压、过载需要满足以下约束：

qi=12ρiV2i≤qmax

Q·I=kQ·ρ0.5iV3.15i≤Q·maxni=X2i+Y2i/（mig）≤nmax （2）

攻角αi（t）和倾侧角σi（t）需要满足：

|αi|≤αmax|σi|≤σmax （3）

（2） 终端约束

对于多枚飞行器协同再入，滑翔段终端条件不仅需要满足速度、高度和待飞航程约束，对于有时间和方向协同要求的飞行器，还需要考虑时间、航向角和视线角的约束：

Vi（ti， f）=V*i

Hi（ti， f）=H*i

si（ti， f）=s*i

ti， f=t*i

ψi（ti， f）=ψ*i

φi（ti， f）=φ*i （4）

式中：航向角ψ定义为飞行器速度方向与正北方向的夹角，以北转东为正；视线角φ定义为飞行器与目标的连线与正北方向的夹角，以北转东为正。

2 带时间和角度约束的三维轨迹规划

将三维轨迹规划过程分为纵向轨迹设计和横向制导逻辑设计两部分。如图4所示，首先，设计攻角剖面求解使纵向轨迹满足时间约束和航程约束的阻力加速度剖面；然后，搜索倾侧角翻转能量点，使三维轨迹满足角度约束；最后，由于飞行器的横向运动会导致终端待飞航程出现误差，因此需要更新阻力加速度剖面，然后再次搜索倾侧角翻转点，经过多次迭代，可以逐步减小误差，得到满足时间、角度约束的三维轨迹。

2.1 基于阻力加速度剖面的纵向轨迹规划

纵向轨迹规划过程主要是设计攻角剖面和阻力加速度剖面，通过跟踪参考剖面得到满足时间、航程等约束的纵向轨迹。

2.1.1 攻角剖面

将飞行器攻角剖面设计为分段形式，参考攻角αc随速度v变化的表达式为

αc=α1         V0≥V>V1α1+α2－α1V2－V1（V－V1）  V1≥V>V2

α2+α3－α2Vf－V2（V－V2）  V2≥V>Vf （5）

式中：V1，V2为中间速度值；α1为大攻角；α2为中间攻角； α3为最大升阻比对应攻角。

2.1.2 阻力加速度剖面

以归一化能量为自变量，将阻力加速度剖面设计为三段折线的形式。阻力加速度-归一化能量剖面示意如图5所示。

图中再入走廊上边界由热流密度、过载、动压约束确定，下边界由平衡滑翔条件确定，计算公式为

DQ·≤CxSQ·2max2mV4.3C2Q·

Dn≤nmaxg1+CyCx2