基于ATB-RRT*与改进DWA的多机器人编队路径规划

摘要：针对多机器人编队规划算法在多障碍物区域路径规划与编队保持能力较弱的问题，提出一种自适应采样目标引力双向RRT*（Adaptive sampling target gravitational bidirectional RRT*，ATB-RRT*） 与改进动态窗口法（Dynamic window approach，DWA） 的融合算法。引入自适应采样与目标引力机制改进双向RRT*算法，改善算法随机性;引入新节点删除策略删除低质量节点，提高算法效率；设计领航跟随型机器人编队控制器，并利用全局路径点改进DWA算法，增强编队在遇到动态障碍后的编队保持能力。仿真实验表明，ATB-RRT*算法相比双向RRT*算法的效率有明显提升，应用改进DWA算法的多机器人编队有较强的编队保持能力。

关键词：多机器人编队；路径规划； ATB-RRT*算法；领航跟随；动态窗口法

中图分类号：TP273      文献标识码：A

文章编号：1009-3044（2023）13-0005-05

开放科学（资源服务）标识码（OSID） ：

0 引言

多机器人编队控制是机器人领域的热点问题，由于要考虑障碍物、编队形成保持等约束，规划编队路径具有一定的难度[1]。多机器人编队控制传统解决方案为通过状态观测器控制编队机器人的角度与距离实现[2]，文献[3]通过增加滑膜模糊积分观测器来应对编队运行中产生的扰动，文献[4]提出了一种基于距离约束的单领航者编队控制算法，通过自适应控制律预估领航者速度保持编队。上述文献虽对编队路径规划有一定作用，但控制方式较为复杂，当需要考虑规划及避障时控制效果无法保证。

RRT算法是一种基于采样的概率完备全局规划算法，在机器人运动规划领域应用广泛，但该算法在多障碍物环境下搜索效率较低[5]。针对上述问题，相关研究者提出多种基于RRT的泛型算法，如具有渐进最优性的RRT*、双树搜索的Bi-RRT*、利用先验信息搜索的Informed-RRT*等算法[6-8]，改善了算法在多障碍物环境的搜索性能。文献[9]通过改进A*全局算法引导动态窗口法，改善动态窗口法对于复杂障碍场通过能力差的问题。上述研究主要针对单机器人规划进行改进，当对象换为多机器人编队时搜索性能改进程度较低。

针对多机器人编队路径规划问题，本文提出一种基于ATB-RRT*和改进DWA的多机器人编队路径规划算法。先后利用ATB-RRT*和DWA规划编队中领航者的路径轨迹，改进DWA算法回归编队路径。实验表明，该算法能为编队规划出成本较低的路径，避障碍后编队保持能力较强。

1 机器人运动学模型

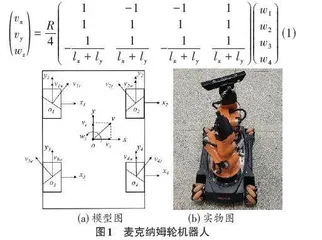
本文采用麦克纳姆轮全向四轮式机器人，机器人模型及实物如图1所示。设轮半径为R，轮子轴线到机器人中心在x与y轴方向的距离分别为lx和ly ，速度分别为vx与vy，机器人绕z轴的角度为wz，四个轮子的线速度与转速分别为vir、wi（i=1，2，3，4）。则机器人运动学方程为：

[vxvywz=R411-1lx+ly-111lx+ly-11-1lx+ly111lx+lyw1w2w3w4]  （1）

基于l-φ型的领航跟随型多机器人编队模型如图2所示。图中Rl、Rf分别为领航与跟随机器人。队形通过控制两者之间的相对角度[φ*lf]与理想相对距离[l*lf]实现，多机器人编队距离公式为：

[lxlf=（xl-xf-dcosθf）cosθl+（yl-yf-dsinθf）sinθllylf=-（xl-xf-dcosθf）sinθl+（yl-yf-dsinθf）cosθl] （2）

式中，d为机器人中心到前侧的距离。

2 ATB-RRT*算法

2.1 自适应采样方法

本文改进采样函数为采样密度与障碍物距离相关的自适应采样，更大概率在障碍物附近产生采样点。采样的概率密度函数p（x，x0，）为：

[p（x，x0，γ）=1πγ（x-x0）2+γ2]       （3）

式中x0为概率密度峰值位置的位置参数，γ为概率密度尺度函数。该函数在x0处达到峰值，左右两侧对称，自适应采样概率密度函数如图3所示。

令[l=x-x0]，其中x为采样点，x0为距该采样点最近的障碍物，则式（3）可表示为：

[p（l，γ）=1πγl2+γ2]            （4）

设置安全距离函数：

[safety（l）=1     （l>α）0     （l<α）]         （5）

式中α表示障碍物与采样点之间的最小安全距离。当[l>α]时，[safety（l）=1]，采样点安全;当[l<α]时，[safety（l）=0]，采样点不安全。采样概率分布函数为：

[P（l，γ）=safety（l） 1-20+∞p（l，γ） dl]   （6）

最小安全距离α与编队中机器人数量呈正相关，单机器人时α值最小。

2.2 目标引力生长机制

生成采样点之后，进入新节点生长环节。随机树从初始点开始，生长新节点Qnew加入树中。基本RRT*算法新节点Qnew的计算公式为：

[Qnew=Qnearest+ρ（Qrand-Qnearest）Qrand-Qnearest]       （7）

式中Qrand为自适应采样的采样点，Qnearest为随机树中距离Qrand最近的节点，ρ为随机树生长的步长。经典RRT*算法中的新节点生长过程如图4（a）所示。

本文根据人工势场法引力思想，改进新节点生长过程。改进后随机树的生长在向采样点方向生长的基础上，增加目标方向的引力分量。加入目标引力的RRT*算法新节点Qnew的计算公式为：

[Qnew=Qnearest+][ρ（Qrand-Qnearest）Qrand-Qnearest+k（Qgoal-Qnearest）Qgoal-Qnearest]   （8）

式中k为引力系数。目标引力RRT*新节点生长过程如图4（b）所示，Qinit、Qgoal为起始与目标节点。

加入目标引力生长机制后RRT*算法节点都具有目标导向性，搜索的随机性降低。由于RRT*算法的目标导向性与避障能力呈负相关，路径避障能力会随之下降，通过调整引力系数k控制生长过程中引力分量的占比来解决这一问题，遇到障碍物时取[k<ρ]，未遇到障碍物时取[k>ρ]。

2.3 新节点删除策略

减少随机树中低价值节点可以增快算法的计算速度。若新节点Qnew符合公式：

[Qnew-Qinit+Qgoal-Qnew>σbest]    （9）

即新节点到起始点与目标点距离之和大于当前最低路径成本，因经过该新节点的路径一定大于等于与起始点与终点的直线距离之和，则删除该节点，式中σbest为当前最低路径代价。

2.4 基于ATB-RRT*算法的全局规划

ATB-RRT*算法利用自适应采样替代随机均匀采样、引入目标引力生长机制引导新节点扩展，降低搜索的盲目性；扩展节点删除策略，提高计算的速度。完整的ATB-RRT*算法流程如图5所示。

以起始点和目标点分别构建两棵搜索树，在环境状态空间内自适应采样获得随机节点Qrand，通过目标引力机制生长出新节点Qnew，利用新节点删除策略判断该新节点价值，若是则删除该节点重新采样，若不是则选取Qnew的邻近节点Qnear，执行重选最优父节点与重布线环节，优化随机树。判断此次采样是否达到迭代次数，达到则结束算法，未达到判断当前随机树Qnew能否与另一棵树最近节点Qother连接，若不能，则继续采样，若能，则比较新连接的路径成本σnew是否小于当前最优路径成本σbest，若不小于，则交换随机树继续采样，若小于，则σnew的值赋予σbest后交换随机树继续采样。

3 编队路径规划

3.1 编队控制率设计

基于领航跟随法设计多机器人编队控制律，将编队系统进行分为领航者与跟随者两层，选取一个机器人作为领航者负责整个编队的路径规划和引导跟随者，跟随者以[l-φ]（距离-角度）的方式对领航者进行跟随，参考坐标为编队领航者。

结合机器人系统模型，并对式（2） 求导，可得：

[lxlf=lylfwl-vfcosδlf+dwfsinδlf+vllylf=-lxlfwl-vfsinδlf-dwfcosδlf]   （10）

[δlf=θf-θl]              （11）

式中，vl与wl分别是领航机器人的线速度与角速度，vf与wf分别是跟随机器人的线速度与角速度。

多机器人编队在领航机器人坐标系下实际相对距离llf与理想相对距离llf*的误差为elf，误差公式为：

[elf=exlfeylf=lx*lf-lxlfly*lf-lylf]          （12）

[lx*lf=l*lfcosφ*lf]            （13）

[ly*lf=l*lfsinφ*lf]            （14）

结合式（10） ，并对式（12） 求导，可得：

[exlf=l*lfcosφ*lf-l*lfφ*lfsinφ*lf-（l*lfsinφ*lf-eylf）wl       +vfcosδlf-dwfsinδlf-vleylf=l*lfsinφ*lf+l*lfφ*lfcosφ*lf+（l*lfcosφ*lf-exlf）wl       +vfsinδlf+dwfcosδlf] （15）

设置领航者与跟随者之间的理想相对距离llf*与理想相对角度φlf*均为一个定值，故把[l*lf=φ*lf=0]代入式（15） ，可得：

[exlf=wleylf+vfcosδlf-dwfsinδlf-l*lfwlsinφ*lf-vleylf=-wlexlf+vfsinδlf+dwfcosδlf+l*lfwlcosφ*lf] （16）

设计控制律：

[elf=-klfelf]             （17）

式中，klf反馈比例系数，公式为：

[klf=k1  00   k2]            （18）

式中，[k1>0]，[k2>0]。

通过式（17） 的控制律，可以使式（16） 的误差值收敛为0，达到领航跟随型多机器人的编队控制。最终跟随机器人[Rf]实现跟随领航者机器人的线速度[vf]与角速度[ωf]分别为：