算法视角下的微积分

摘要：文章内容包含高级语言中的函数概念、函数的改变量（增量）是贯穿微积分始终的线索、定积分的近似计算。主要结论是：微积分就是一个大算法，是一系列演算法则的集合。文章强调了微积分的抽象之美、演绎推理之美、空间想象之美、应用之美等，对微积分教学、程序设计教学有一定的参考价值。

关键词：算法；微积分；函数；近似计算；边际与弹性

中图分类号：TP311      文献标识码：A

文章编号：1009-3044（2023）26-0016-03

开放科学（资源服务）标识码（OSID）

微积分的英文名称——calculus，来源于拉丁文中的“石子”“演算”词语，换句话说，微积分的本质就是一种演算法则或计算方法。因此不要觉得微积分有多神秘，它就像大家熟知的加减乘除四则运算一样，只是众多计算方法中的一类算法而已。

从微积分字面释义来看：微分——顾名思义就是事物微小的部分——事物似零非零的部分，这个似零非零的部分从哪里而来？它是从某个事物整体无限细分得来，这是化整为零的过程；而积分——它是积累、累积的部分，是无限求和的过程。和之前正好相反，它是求微小部分的和，也就是求似零非零部分的和，这是积零为整的过程。微元法是用定积分解决实际问题的基本思想、基本方法，其本质就是先化整为零，再微元替代，最后积零为整。

1 高级语言中的函数概念

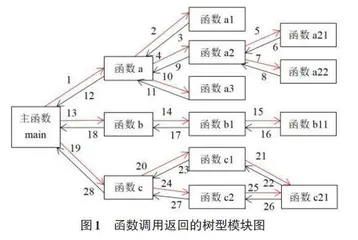
函数是微积分的主要研究对象，函数的极限、函数的连续、函数的导数与微分、函数的积分是贯穿微积分始终的内容。函数是科学史上流行了200多年的一个基本概念，因此深刻地影响了其他学科……计算机过程化高级语言中的函数其实就是程序代码中的子程序，更有甚者C语言里的主程序也是函数（main（）主函数），强大的高级语言的一个重要指标就是它拥有丰富的内部函数。图1是C语言中的一个函数调用返回的树型模块图[1]。

函数调用返回、参数传递、局部量与全程量、嵌套调用与递归调用等是很多高级语言的重点和难点[2]，教学过程中学生往往感到困惑和无所适从，但从微积分的角度看，也就是一个有限次的多重复合函数而已。

2 函数的改变量（增量）是贯穿微积分始终的线索

函数的改变量（增量）是贯穿微积分始终的线索，而编程计算函数增量很简单。函数改变量（增量）的定义如下：设x0为函数y=f（x）定义域内一点，自变量x在x0处取得增量Δx，Δx= x-x0，x = x0+Δx在定义域内，则f（x0+Δx）- f（x0）称为在x0点的函数增量（或改变量），记为Δy。用示意图表达如下[3]：

[函数y=f（x），由自变量增量Δx产生函数增量Δy，x0→x0+Δx........Δx↓........↓........↓f（x0）→f（x0+Δx）...Δy=f（x0+Δx）-f（x0）]

用函数图形表示如下（含[Δx>0]和[Δx<0]两种情形）：

下面将会看到微积分中的重要概念和内容和函数增量有关：

1） 函数连续的定义：[f（x）]在[x0]处连续[⇔limΔx→0Δy=limΔx→0（f（x0+Δx）-f（x0））=0]

定义说明函数连续表达的是自变量的微小变化只会引起对应函数的微小变化。

2） 函数导数的定义：

[f（x0）=limΔx→0ΔyΔx=limΔx→0f（x0+Δx）-f（x0）Δx]

从定义可看出导数描述的是函数变化率这一概念，不管自变量和因变量代表的是几何量或物理量，导数纯粹从数量角度刻画函数变化率的本质： 函数增量[Δy]和自变量增量[Δx]的比值[ΔyΔx]是函数[y]在以[x0]和[x0+Δx]为端点区间内的平均变化率，导数[y|x=x0]则是函数[y]在[x0]点处的瞬时变化率，反映了函数[y]随自变量[x]变化而变化的快慢程度。

根据导数的定义，函数求导的算法步骤如下：

①计算函数的增量：[Δy=f（x+Δx）-f（x）;]

②计算两增量的比值：[ΔyΔx=f（x+Δx）-f（x）Δx]；

③计算极限值：[y=limΔx→0ΔyΔx。]

3） 函数微分的定义：设函数[y=f（x）]在某个区间上有定义，[x0]和[x0+Δx]在此区间内，若函数增量[Δy=f（x0+Δx）-f（x0）]可表示为 [Δy=A⋅Δx+o（Δx）]，这里A是和[Δx]无关的常数，则称函数[y=f（x）]在[x0]点处可微，并称[A⋅Δx]为函数[y=f（x）]在[x0]点相应于自变量增量[Δx]的微分，记作[dy]，即：[dy=A⋅Δx]。

将以上定义通俗化，如果在某点的函数增量Δy用自变量增量Δx线性表示，误差仅是Δx一个高阶无穷小，则称函数f（x）在此点可微， 微分[dy]即是函数增量Δy的线性主部。

重要定理：函数[y=f（x）]在[x0]点处可微的充要条件是它在[x0]点处可导，而且微分和导数关系是：[dy=f'（x0）⋅Δx][3]。

由此定理可得：[dx=Δx]。这样函数的导数其实是函数微分与自变量微分的商。即[f（x）=dydx]，因此导数也称为“微商”。

[Δy=AΔy+o（Δx）→dy=AΔx⇒dy=f'（x0）Δx⇒dy=f'（x0）dx→dydx=f'（x0）]

4） 导数在经济学中的应用——边际与弹性

边际与弹性从语义上理解，只能是指定状态下的微小改变。这里反映的是函数的绝对变化率和相对变化率（绝对导数与相对导数）。具体概念对比表述如下：

设有经济函数[y=f（x）]可导，当自变量发生改变[x→x+Δx]，其自变量绝对改变量为[Δx]，函数的绝对改变量为[Δy=f（x+Δx）-f（x）]，绝对平均变化率为[ΔyΔx]，取极限就是绝对变化率，就是函数[f（x）]在点[x]处的边际，记为：

[ddxf（x）=dydx=f'（x）=limΔx→0ΔyΔx=limΔx→0f（x+Δx）-f（x）Δx]

取[Δx=1]，即自变量在[x]处改变一个单位时，若这个“单位”很小或相比[x]值很小时，则：

[f'（x）=limΔx→0f（x+Δx）-f（x）Δx≈f（x+1）-f（x）1=Δf，]

即Δf≈f’（x），此式的意义是：当自变量在x处改变一个单位时，函数f（x）的改变量可近似用f’（x）来表示，即改变了f’（x）个单位，此为边际的经济意义。

设有经济函数[y=f（x）]可导，当自变量发生改变[x→x+Δx]，其自变量相对改变量为[Δxx]，函数的相对改变量为[Δyy=f（x+Δx）-f（x）f（x）]，相对平均变化率为[Δy/yΔx/x]，取极限就是相对变化率，就是函数[f（x）]在点[x]处的弹性，记为：

[EExf（x）=EyEx=limΔx→0Δy/yΔx/x=limΔx→0ΔyΔx.xy=y'xy]

取[Δx/x=1%]，即自变量在[x]处相对改变 1% 时，

[EyEx=limΔx→0Δy/yΔx/x≈Δy/y1%，]从而[Δy/y≈EyEx%][4]。

上式的意义是：当自变量在x处相对改变1%时，函数f （x）的相对改变量大致为 Ey/Ex%，此为弹性的经济意义。

5） 不仅微积分上述的基本概念和函数改变量有关，微积分中重要的定理、公式也和函数改变量有关。比如：拉格朗日中值定理：[f（b）-f（a）=f'（ξ）（b-a）]。

柯西中值定理：[f（b）-f（a）g（b）-g（a）=f'（ξ）g'（ξ）]

牛顿—莱布尼茨公式：[abf（x）dx=F（x）|ba=F（b）-F（a）]

结论：函数的改变量（增量）是贯穿微积分始终的线索。这部分涉及的极限运算可用高级语言中的循环结构实现，由循环语句中的条件表达式控制精度。

3 定积分的近似计算

定积分是积分学中重要的内容，起源于生产实践中面积和体积等的计算问题。回顾初等数学中面积计算的相关内容：（由）长方形面积的定义→（推出）平行四边形面积公式（拼接法）→（推出）三角形面积公式（拼接法）→（推出）梯形面积公式（拼接法）→“穷竭法”“割圆术”得到圆面积公式。数学中的重要概念并非无中生有，而是从客观世界的现实原型中抽象出来的，比如“曲边梯形的面积问题”“变速直线运动的路程问题”都是定积分的现实原型，抽象得到的定积分定义后，数学家们辛勤探索得到定积分的性质、定理、公式等，理论完善后再应用现实原型中。整个过程中有抽象之美、演绎推理之美、空间想象之美、应用之美等。定积分在微积分中是需要花时间讲清楚的概念，其严格定义简述如下[4]：

定义 设函数[f（x）]在闭区间[[a，b]]上有界， 在[[a，b]]中任意地插入若干个分点[a=x0<x1<x2<...<xn-1<xn=b] 把闭区间[[a，b]]分割成了n个小区间[[x0，x1]]， [[x1，x2]]， [...，] [[xn-1，xn]]，各个小区间长度依次记为[Δx1=x1-x0，] [Δx2=x2-x1，][...，Δxn=xn-xn-1]。在每个小区间[[xi-1，xi]]中任意取一点[ξi （xi-1≤ξi≤xi），] 将函数值[f（ξi）]和小区间长度[Δxi]的乘积[f（ξi）Δxi][（i=1，2，...，n）]全部相加，得到和式[Sn=i=1nf（ξi）Δxi，]记[λ=max{Δx1，Δx2，...，Δxn}，]假若无论对[[a，b]]怎样的划分， 也无论在小区间[[xi-1，xi]]上[ξi]点怎样取法， 只要当[λ→0]时， 和[Sn]必将趋于确定的极限I， 这个极限I就称为函数[f（x）]在区间[[a，b]]上的定积分， 记成：

[abf（x）dx=I=limλ→0i=1nf（ξi）Δxi]，

其中[f（x）]称为被积函数， [f（x）dx]称为被积表达式， x称为积分变量， [[a，b]]称为积分区间。

问题的提出：如何计算[abf（x）dx？]有以下解决思路：1） 显然可由定义求和式的极限得到，但这样太麻烦，有些和式极限还要转换成定积分来求。2） 利用定积分的几何意义得，但仅适用于被积函数简单情形。3） 牛顿—莱布尼茨公式[abf（x）dx=F（x）|ba=F（b）-F（a）]是计算定积分的有力工具，但应用该公式必须找到被积函数的原函数，也就是要先求不定积分，而有些函数的原函数是不能用初等函数表示的，属于“积不出来”的积分，这个时候只能考虑利用计算机进行近似计算。定积分的近似算法有矩形法和梯形法，算法思路如下[5]：

[abf（x）dx=limλ→0i=1nf（ξi）Δxi]

由于对于任意的分法结果一样，可等分区间得：

[abf（x）dx=limn→0b-ani=1nf（ξi）]

近似公式为：

[abf（x）dx≈b-ani=1nf（ξi）]

上式n足够大就能保证足够的精度。由于对于任意的取法结果一样，[ξi]可取左端点或右端点，得到左矩形公式[abf（x）dx≈b-ani=1nf（xi-1）=b-ani=1nyi-1] 和右矩形公式[abf（x）dx≈b-ani=1nf（xi）=b-ani=1nyi]，若小矩形用小梯形替代，则得到梯形公式：

[abf（x）dx≈b-an*12i=1n（f（xi-1）+f（xi））=b-ani=1n（12y0+y1+y2+...+yn-1+12yn）]。

实例：用矩形法和梯形法计算定积分[01e-x2dx]的近似值。