借小课题研究，提升儿童数学理性思维的品质

【摘要】随着核心素养教育理念及“双减”政策的不断落实，作业的优化设计成为小学教育的重点改革方向之一。教师应聚焦学科核心素养，重视当前“立学课堂”的变革，设计既能帮助学生巩固所学知识、内化知识难点，又能提升学生思维能力和学习能力，促进学生实现全面发展的多元化作业。

【关键词】数学理性思维；作业设计；课题研究；小学教学

作者简介：朱建美（1972—），女，江苏省南通师范学校第二附属小学。

作业作为课堂教学的延伸与拓展，是学生获取和应用知识的有效手段。在完成作业的过程中，学生经常会遇到感兴趣但却难以解答的拓展问题，究其原因是学生不懂得有效联系和归类，加上知识储备不足，导致思路分散，难以顺利解题。针对这种现象，笔者尝试让学生通过完成专题探究任务来巩固并建构相关知识，从而内化学习难点。以“长方体、正方体上切挖”问题为例。笔者设计了由“题”到“题组”，再到“题组模块”的小课题研究任务，以“练习串”的形式，使各练习题之间有效串联，在串联中体现题目层次的变化，让学生挖掘“切挖”与“叠加”知识及思维方法之间的内在联系，培养学生对比联结意识和整体建构意识，从而提升学生的数学思维品质。

一、作业设计的目标

其一，学会分析“长（正）方体上切挖小长（正）方体”表面积、体积变与不变中的数量关系；感悟平面图形与立体图形中变与不变的对应关系；合理转化“切挖”“叠加”问题，灵活选择方法正确计算表面积、体积。

其二，通过专题练习，培养学生对比分析、有效联结、整体建构的能力，提升学生严谨、理性的数学思维能力。

其三，激发学生探究的兴趣和愿望，同时渗透学科育人的思想，提高学生完成练习的积极性，培养学生的科学态度，发展学生推理能力和空间观念，提升学生解决问题的能力。

二、作业设计的策略及意图

（一）思维需要步步入，培养线性逻辑

1.顺学而设，促进有效学习

教师要关注学生的真实情况，给学生充分观察对比、分析思考的机会，提高学生发现“真相”即“有效联结”的可能性。设计作业前，教师应对学生的知识基础、学习方法、理解能力、学习兴趣、态度等学情进行调查。只有基于学情，立足知识生长点，才能设计出符合学生能力发展需求的作业。

例题1：平面图形周长、面积的变化

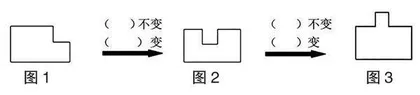
从一个长3.5厘米，宽2厘米的长方形的边上剪去一个边长1厘米的正方形（见图1），剩下图形中的周长有什么变化？面积呢？将图2分割掉的小长方形往上平移变成图3所示图形呢？

设计意图：旧知铺垫，助力发现新知。复习平面图形的相关知识点，既是帮助学生查漏补缺、温故知新的过程，也是为学生数学探究建立有效联结，做好学习情感上的准备的过程。

例题2：立体图形表面积、体积的变化

（1）将一个棱长20厘米的正方体分别从一个顶点、一条棱、一个面上切去一个棱长5厘米的小正方体后，剩下立体图形的表面积分别是多少？体积呢？

（2）在一个棱长为a的大正方体中，挖去一个棱长为b的小正方体。图4中剩下图形的表面积为（ ）；图5中剩下图形的表面积为（ ）；图6中剩下图形的表面积为（ ）。

A.6a2 B.6a2+b2 C. 6a2+2b2 D.6a2+4b2

设计意图：学生在分析、计算、对比中易于发现，用不同方法切挖后，剩下立体图形的表面积、体积的规律，这有利于学生更好地理解并区别表面积、体积，掌握表面积与体积的算法。用字母算式抽象概括表面积、体积的算法，这种对比学习的方式可以增强学生的发现意识及自主归纳概括意识，使学生初步感悟从二维到三维，变与不变的对应关系。

2.迁移方法，思维更具理性

教师要从作业设计上寻找提升教育质量的切入点，让作业充分体现出数学知识、思想的应用价值。作业设计要精巧，教师只有充分把握了作业设计的主题思想，才能科学地设计作业，在作业中合理地、循序渐进地渗透数学思想，让外显的数学知识与抽象的思维方法齐头并进，达到“润物细无声”的教育效果［1］。

例题3

设计意图：例题3从常式练习过渡到变式练习，让学生借助直观图像再次分析比较、归纳概括剩下图形与原长（正）方体的表面积、体积的变与不变关系，在切挖前后图形表面积、体积变化的数量关系分析中，增强学生数形结合的意识及归纳概括能力，在强化对知识的理解和应用的同时，提升学生的理性思维能力。

例题4：两块同样的长方体木块，长是20厘米，宽是10厘米，高是8厘米，分别从两木块的顶点处、棱上切下一个最大的正方体后，剩下部分的表面积分别是多少平方厘米？（先画图再列式计算）

设计意图：学生根据题意画图，边画边思考，数形结合，让隐性的思维借由显性的图形表现出来，让抽象的算式看得见、理得清。学生根据空间想象将立体图形正确地描绘出来，借“画”力助长学力，在动手操作中助推空间想象能力的培养，进一步发展空间观念。

（二）思维考量向度多样化，提升思维品质

教师对学生思维的考量应是多角度的，比如思维的深刻性、广阔性、敏捷度、灵活性、独创性、批判性、逻辑性等。因此，教师应在作业设计中融入高质量的思维活动，让学生在思维活动中形成深刻的数学思想。这样的作业设计才能发挥教育的实效，提升学生的思维能力。

1.设计分层作业，关注学习进阶

每个学生的个性、学习水平、能力有所差异。教师要尊重学生的个性差异，设计分层作业，关注学生在学习中的进步，满足不同学生的学习需求和挑战欲望，保证各层次学生都能在作业完成过程中提高思维的清晰度、深度、广度等。同时，教师要鼓励学生以小组的形式展开互助学习，让每位学生都能在小组合作中得以展示、表现，增强学习信心，满足学习情感需要。

例题5：

（1）一个3分米的正方体，分别在前后、左右、上下各面的中心位置，挖去一个棱长1分米的小正方体，挖完后得到的形体，它的表面积是多少平方分米？体积呢？

（2）在一个棱长为1.5分米的正方体零件的6个面的中心分别向对面挖穿一个横截面是边长5厘米的正方形孔。求零件的表面积是多少？体积呢？

设计意图：笔者设计了两道难度进阶的题目，引导学习能力较弱的学生完成第（1）题，引导学习能力较强的学生依次完成这两道题。同时，鼓励学习能力强的学生作为组长，带领学生能力较弱的学生完成对第（2）题的探究，让全体学生都能实现能力的生长。学生在共同参与、互动交流、彼此质疑的头脑风暴中，互帮互助，真正实现个性化学习。

2.融入生活元素，走近数学本质

在作业设计中，教师要融入生活元素，让学生在解题过程中感知数学知识在生活中的应用价值。对此，教师可以多设计一些突出个性思考的主观题，考验学生的分析能力和应用能力等思维品质，让学生意识到数学在生活中大有用处［2］。

例题6：

（1）友联木材加工厂想给贫困学校赠送学具，计划将一块长20厘米、宽15厘米、高10厘米的长方体木料加工成下面的多面体（见图9），上面两个小正方体的棱长分别是1厘米、2厘米，你能算出这个多面体的表面积、体积吗？ 你认为木材厂的加工方法合理吗？说说你的理由。

（2）分别用两个、三个正方体木块堆成如下多面体，算一算两个多面体的表面积与体积。

设计意图：学生可以在解决第（2）题的基础上去解决第（1）题中的“长方体叠加问题”，深入思考“切挖”与“叠加”算法的联系，并联想到实际生活中建筑高楼中的一些开放设计：长（正）方体的错位堆叠。学生通过计算还发现，从大长方体上切挖出这个多边形，太浪费木材，木工厂需要考虑木材加工成本。由此，学生进一步理解了数学在生活中的应用价值。

（三）思维需要网状发散，凸显知识结构性

数学的理性体现在知识的本质性、规律的普遍性和方法的简捷性等方面。优秀作业可以与教学相得益彰，在学生探究过程中揭示知识的本质和普遍的规律，提炼简洁、理性思维方法，让学生的数学理解更深刻、更通透。

1.做中反思，合理转化思维方法

学生在完成作业的过程中，需要展开自我反思，这是一种必备品质。基于“叠加”思想的变式运用，教师可设计与“切挖”有关的星数题组，激发学生潜能，让学生在问题解决中进一步感悟“切挖”与“叠加”思想转化的合理性，让不同学习能力的学生在深度思维活动中解决并内化知识难点，实现思维水平从量变到质变的飞跃。

2.问题引领，思维串紧“知识线”

学生的学习经验与建构能力有限，对问题的认识往往是具体的、特殊的、局部的。教师要以系统化、整体化的视角，帮助学生对问题做普适化的归纳与提炼，让知识形成良好的关联，凸显知识的结构性和生成性，让学生感受数学的理性精神，逐步养成数学的意识与眼光，从而实现数学素养提升。

例7：仔细观察图12，你有进一步的发现吗？填一填。

设计意图：在上述例题中，学生经历二维到三维的对比观察，感悟面积与体积、周长与表面积的变与不变，在变化中找到不变元素，分析原因，进而同化类似知识经验，完善已有的知识结构、思维结构，达到提升思维能力的目的。

（四）思维聚焦核心知识，培养创新思维

教师聚焦本课的核心知识，设计开放性的实践作业，让学生的学习状态从封闭走向开放，不仅能激发学生的学习兴趣，还能挖掘学生的内在潜能，培养学生的创新思维。

例题8：根据“切挖”思想研究所得，用橡皮泥捏一个立体图形并进行切挖、编题、解答。

设计意图：本题以“基本形体切挖”为载体，结合美学，鼓励学生设计个性化的习题，重在培养学生的空间想象力和塑形能力。在实践过程中，学生会创造出多种多样的习题，而教师则要耐心倾听学生的设计想法并指导学生，帮助学生设计出有创意、有审美的数学题。

结语

在小学数学教学中，作业设计应强调知识的关联性、理性的思维，体现知识、思维的整体架构，让学生在充分经历类比联想、深度探究、有效拓展、实践创新的过程中，实现思维层层进阶，感悟学习其实就是探秘并不断揭秘的过程。在解题实践的过程中，学生的思维品质得以提升，创新精神得以体现。

【参考文献】

［1］朱玉杰.单元作业设计的尝试与反思［J］.中学数学教学参考，2021（20）：76-78.

［2］周卫东.为品格而教［M］.南京：江苏凤凰教育出版社，2021.