关联视角下运算教学的问题诊断与对策研究

【摘要】运算是数学的重要内容，运算能力的培养与发展是一个长期的过程。数学教师要在小学数学轻负高质理念的引领下，逐步培养和发展学生的运算能力，提升学生的运算素质，让学生掌握由具体到抽象，由法则到算理，由单项思维到逆向、多向思维的运算技能。文章关注第二学段数学运算知识点之间的关联，从整体视角梳理小学运算知识点，重点抓好运算种子课的教学，培养学生转化、迁移、类比等数学思想，提高学生的运算能力和素质。

【关键词】关联视角;运算教学;问题诊断;对策

作者简介：汪利锋（1977—），男，浙江省杭州市富阳区富春第八小学。

一、运算教学的问题

《义务教育数学课程标准（2011年版）》中关于运算的描述是：“运算是数学的重要内容，在义务教育阶段的数学课程的各个学段中，运算都占有很大的比重，学生在学习数学的过程中，需要花费较多的时间和精力去学习和掌握关于各种运算的知识和技能。”然而在当前的运算教学中，教师缺乏从整体视角来审视运算教学的意识，运算教学碎片化，缺少关联式教学。因此，笔者结合当前运算教学现状，梳理第二学段运算知识之间的关联，为整体运算教学实践研究提供建议和参考。

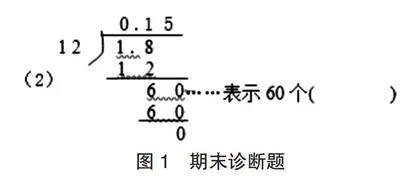
例如，在某次区五年级期末诊断卷中，考查小数除法中除得的余数意义（图1），全区得分率在51%左右，充分反映出学生对该知识点掌握不深。教师如果能在新课教学时引导学生联系三年级下册整数除法中的余数的意义（图2）和四年级下册小数的计数单位的理解（图3）这两部分内容来学习该知识点，就能让学生更好地理解和掌握这一知识点，相信再遇到此类题目时，学生一定能答对[1]。

二、第二学段运算知识点关联梳理

笔者对小学第二学段运算的知识点进行梳理后发现，四至六年级有许多相关联的运算知识点，它们无论是在算法、算理上，还是在运算定律上，都具有密切关联。教师从整体视角来梳理运算知识点，在运算教学中将相关联的知识点串联起来，对学生算理理解、算法掌握、规律的迁移等知识的学习都具有非常大的帮助。

（一）梳理运算知识点之间的关联的意义

所谓关联，是指事物相互间产生的影响和牵连。教师要从小学数学教材中寻找各年级运算知识点之间的联系。教师借助学生已掌握的相关知识来帮助学生理解新知识，这是承前;教师在教学时将目光延伸得更长远，这是启后。厘清小学第二学段运算教学中的关联，对教师整体把握运算教学具有较大帮助。

（二）第二学段运算关联知识点梳理

笔者梳理了四至六年级运算教学关联知识点的分布（图4）。

从图4可知，四年级上册整数笔算乘法和五年级上册的小数笔算乘法、小数笔算除法，无论是在算理上，还是在算法上，都具有紧密的联系和可迁移性。学生对整数乘除法的掌握程度，将直接影响到五年级的小数乘除法的教学。

笔者发现，四年级下册的加法运算定律（加法交换律、加法结合律）和小数加减法运算定律、五年级下册的分数加减法运算定律之间存在关联，四年级下册的乘法运算定律（乘法交换律、乘法结合律、乘法分配律）和五年级上册的小数乘法运算定律、六年级上册的分数乘法运算定律同样也存在联系。学生对整数运算定律本质属性的理解和对运算定律的掌握程度，将影响到小数和分数运算定律的教学效果[2]。如五年级下册的分数加减法是一个脱离自然数运算的全新运算知识，教师要结合加法运算定律，帮助学生更好地学习分数加减法。

（三）厘清关联，上好运算教学种子课

进行第二学段运算教学时，教师要站在整体视角来分析整个第二学段的教材，厘清运算知识点之间的关联。以四年级的“三位数乘两位数”教学为例，该知识点与五年级的小数乘法具有密切联系，教师在教学三位数乘两位数时，若能帮助学生明晰算理、夯实算法，当学生学习小数乘法时，在理解算理和掌握算法的基础上就能轻松掌握该知识点。

再如，上好四年级种子课—整数的乘法运算定律教学，对五年级上册将运算定律推广到小数教学，六年级上册将运算定律推广到分数教学具有重要的影响（图5）。因此，教师在教学四年级种子课时，一定要通过具体的情景，让学生了解和掌握运算定律，培养学生的代数思想，让学生可以用字母表示运算定律，这能为学生五、六年级的学习打下良好的基础，取得事半功倍的教学效果。

在数学学习中，转化的思想十分重要，要求学生利用已学的旧知识来解决新问题。因此，教师要认识到运算种子课教学的重要性，重视运算种子课，在种子课上讲透算理、讲清算法，为学生的后续学习打下良好基础。教师切勿在起始教学时就产生学生没掌握这节课的知识不要紧，可以后面慢慢补的想法，须知学生后半程的运算学习在很大程度上要借助前半程的基础，如果前面的知识学得不扎实，后面的转化学习就无从谈起。

三、第二学段运算关联教学的实践研究

（一）在运算教学中运用算理的关联

在人教版五年级上册第三单元“小数除法”例1（图6）中，余数的意义是小数除法教学的难点，要让学生充分理解小数除法中每次除得的余数的意义，教师可以在教学前引导学生回顾三年级下册学过的整数除法中余数的意义和四年级下册关于小数计算单位的理解这两部分知识（图7、图8），然后让学生进行知识的迁移，理解小数除法中余数的意义。

我们可以发现，除法中每次除得的余数的意义，在三年级下册就已经出现过，教师在教学时可以用数形结合的方式让学生理解每次除得的余数的意义。

类似的算法关联在加减法中也有体现，例如六年级上册异分母分数加减法的教学，教师在梳理算理的时候，要发现整数、小数和分数加减法之间的算理关联点（图9），让学生明白不同数的加减法具有共同的算理：整数、小数、分数的加减法都是把计数单位相同的数相加减。

（二）在运算教学中运用算法的关联

算法迁移在小学第二学段的运算教学中有非常明显的运用。从图4运算教学知识点关联的梳理中不难发现，四年级上册和五年级上册这两册教材中关于算法的教学有高度可迁移性。

教师在教五年级的小数乘法和小数除法时，要将四年级整数乘法和整数除法的方法迁移过来（图10、图11）。小数乘法的知识建立在整数乘法和小数的意义的基础上，小数除法的知识建立在整数除法和商不变的性质的基础上。由此可见，四年级上册的三位数乘两位数和除数是两位数的除法，是后续阶段整个乘除法的种子课，学生在种子课上对算理的理解和算法的掌握，直接决定了学生的乘除法运算能力。

（三）在运算教学中运用运算定律的关联

在五年级运算定律的教学中，教师要善于运用运算定律的关联，例如积的变化规律和商的变化规律（包括商不变性质）等。

五年级教材中积的变化规律没有列入例题教学（新课教学），而是在教材中（图12）以练习题的形式呈现，编写教材的专家把积的变化规律放在了四年级上册教材中（图13）。同样，商的变化规律出现在了五年级上册教材的练习题中（图14、图15）。因此，该知识的教学仍然要回到四年级上册[1]。

回到教材，笔者发现，商不变的性质这一知识点仅出现在五年级上册教材的练习题中，而在四年级上册教材中以例题形式呈现，以较多篇幅让学生理解和应用商不变的性质。可见，教材编写者认为，商不变的性质这一内容应让学生在四年级就掌握与夯实，而五年级小数除法的商不变的性质教学已经属于知识迁移的范畴，无须在新课教学中展开。而六年级学生在探究分数除法的运算方法时，除了画图表示，更多同学是用乘除数倒数的方法来运算，将商不变的性质知识继续迁移到分数除法的运算中。

如图15的例题，学生在自主探究时往往会利用四年级学习的商不变的性质，让被除数和除数同时乘一个不为0的数，使除数变成1，突破分数除法的难点，把握乘倒数的本质。学生一般都会这样表示：÷=（×）÷（×）=（×）÷1=2。由此可以看出，学生在学习新知识时会将已掌握的相关知识进行迁移，教师运用运算定律的关联进行教学，有利于让学生更好地理解和掌握知识[3]。

综上所述，教师要从整体角度分析与研究教材，厘清第二学段中运算知识点之间的关联，从运算的算理、算法和运算规律等方面入手，上好运算教学的种子课，培养学生转化的数学思想以及抽象思维能力和演绎能力，从而提高学生的运算能力，让学生更好地理解和掌握运算知识。

【参考文献】

[1]刘学华.小学数学计算错例分析与对策研究[J].试题与研究，2021（27）：39-40.

[2]李莹.“问题导学”视角下学生运算能力的培养研究[J].东西南北，2019（12）：152，151.

[3]马朝云.分数运算教学存在的问题与对策探析[J].成才之路，2021（09）：90-91.