基于PDR/WIFI组合室内定位方法研究

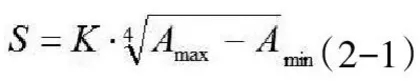
摘 要：随着WiFi的普及，信号范围覆盖越来越广，基于WiFi的室内定位可以实现复杂环境中的定位，定位成本也会越来越低，但仍存在信号容易被遮挡而导致定位随机性大的不足。当下，智能手机配备了各种传感器，让基于惯性传感器的定位技术成本变得很低，且具有实时定位目标的优点，但是存在较大的惯性累积误差。所以利用行人航位推算（Pedestrian Dead Reckoning，PDR）和WiFi定位融合的方法可以提高定位精度。

本文首先对行人航位推算进行研究，解决航位推算的三个关键步骤：步频检测、步长估计、角度偏移。步频检测主要通过加速度变化判断行人行走步数。步长估计主要通过线性步长模型来进行估计。角度偏移只需要通过惯性传感器测量得到角度变化。然后，研究WiFi定位方法，利用衰减模型计算与AP距离，然后通过最小二乘法定位出坐标。最后通过扩展卡尔曼滤波解决非线性问题，将航位推算方程作为观测方程，WIFI定位坐标作为量测方程，实现二者数据融合。

通过MATLAB绘制WIFI定位和PDR/WIFI融合后定位的行为轨迹，发现融合后的结果更接近真实行为轨迹。通过PDR/WIFI组合进行室内定位提高定位精度，能更好地应用于商场、地下车库等室内场所。

关键词：室内定位; WiFi; PDR; 扩展卡尔曼滤波

中图分类号：P228         文献标识码：A        文章编号：1006-3315（2021）11-225-003

1.引言

随着定位技术的飞速发展，位置服务已经成为人们日常工作、生活所必须的一项基本服务需求。当前，室外定位技术已经比较成熟，相比之下，室内定位技术才刚刚起步，而人们对室内定位的需求也日趋明显。提高室内定位的精度，能更好地应用于商场、地下车库等室内场所。目前，研究室内定位的常用技术分为两类：一是基于无线信号的定位技术，如射频识别技术、WiFi技术等;二是基于非电信号的定位技术，如地磁场技术、惯性测量技术、超声波技术等^[1]。查峰，覃方君等人研究发现惯性导航在短时间内的定位精度很高，但具有误差累积效应^[2];而黄威，张玲华等人研究发现WiFi定位的精度虽不如前者高，但不存在误差累积^[3]。本文主要是使用惯性测量单元在行走过程中的加速度、角速度等数据，利用这些数据对行人进行步长和方向的推算;WiFi定位主要是通过RSSI来测算行人的位置坐标。传统的卡尔曼滤波只能解决一些线性问题，而此时研究的问题是存在方向角变化，是非线性模型，所以要进一步采用扩展卡尔曼滤波，通过积分转化为线型模式来进行数据的融合。

2.PDR定位原理及过程

2.1PDR原理

行人航位推算是依靠行人行走的步长S已经航向角θ来推算坐标位置的^[4]。但是，其中的步长S的推算不能简单地通过对加速度的二次积分来获取，因为前文提到这样会使测量的误差累积，很大影响定位精度。所以想要更科学的计算步长，要利用行人行走动力学，根据每个人的步态特征，统计出行走步数，再利用模型估计行人每一步的步长，累积进而获得行走的距离^[5]。

2.2航位推算三个数据获取

2.2.1步态检测

利用零点交叉法，即根据行人行走时总是要经历一个加速和减速的过程，随着脚后跟离开地面，会产生加速效果，同一只脚脚后跟再次着地时会产生减速效果，所以在剔除重力加速度后，运动的加速度值会有正负值，正表示加速，负表示减速，因此确定波形的零点就可探测跨步的起始点^[6]。

2.2.2步长估算

利用非线性步长模型。由于没有充足的理论证明步长与统计特征值之间的线性关系，所以一些研究者就探究了一些非线性模型，如含有一个参数的非线性模型，其公式为：

由此公式看出，只要统计了最大和最小加速度，将其中的参数K计算出来，就可以完成估算^[7]。根据各项数据多方面考虑，最终选定K值为0.52最合适^[8]。

2.2.3偏移角计算

首先，选定一个测试环境，从正西方向到正东方向来回走动，将测量结果在MATLAB中绘制出来，发现X轴角速度变化明显，故可以选择X轴方向为参考方向。故选取X轴的波峰作为角度偏移角。根据测量的数据将三个方向的角速度变化在MATLAB中绘制出来，就可得到角度偏移。如果波峰不是很明显，也可以设定一定的角度变化作为阈值来筛选角度变化率，进而算出角度偏移角。角度变化率较小的视为行人行走时沿上一时刻方向直线行走。

3.WiFi定位原理和计算方法

3.1衰减模型定位

因为现实的室内环境复杂，存在许多遮挡信号传播的物体，信号也会多路径传播，查找文献发现研究者研究出了对数距离路径衰减模型，公式如下：

PL（d）（dBm）=PL（d₀）+10·n·log（d/d₀）+FAF（3-1）

PL（d）为传输的损耗值，也就是定位装置距离已知AP点一米位置的信号损耗值，n为衰减因子，将环境氛围分为全开放、半开放、较封闭场景，不同的场景，衰减因子取值不同，FAF是穿透建筑物的损耗。

将模型简化为以下公式：

P_r（d）=RSSI=A-10·n·logd（3-2）

其中，n为衰减因子，不同环境下衰减因子的取值不同

本文的衰减因子取2.2，公式中另外一个参数值A需要在AP周围进行测量确定其值。本文通过在AP附近设置3个测量点，在每个测量点测量采样40组RSSI数据，然后将采集的数据根据从小到大排列，从中间开始向两边选取40个RSSI数据，最后取其平均值作为A的最终值。从采集的数据中算得，此时A的值为-38，故公式（3.2）可改写为

RSSI=-40-2l·log（d）（3-3）

则只需测量RSSI值，通过公式（3.3）就可以直接计算出采集装置位置与AP之间的相对距离^[9]。

3.2衰减模型的算法定位

当含有三个AP的实际情况下，采集装置的位置坐标不再是三个不同半径的圆周的交点，而是在近似三角形的ABC区域中。所以，要想得到采集装置的具体位置，需要建立方程式，将待测目标的坐标作为未知数，求解该方程式的解。利用最小二乘原理解得：z=（A^TA）^-1A^Tb（3-4）

用公式（3-4）可以解得z，即待测目标处的位置坐标（X，Y）^[10]。其中A为系数阵，b为参数阵。

4.扩展卡尔曼滤波原理及融合过程

对于一般的卡尔曼滤波方程组，想要进行最优估计递推，就必须要求状态方程和量测方程都是线性方程，而在室内定位数据的融合中，行人航位推算的方程式非线性的，因此，一般的卡尔曼滤波不适用于本文研究的非线性方程系统。所以针对这种情况，常用的方法是将非线性方程转化为线性方程，利用泰勒公式的一阶线性形式，将非线性方程转化为线性方程。关键步骤是利用泰勒公示的一阶线性公示获得状态转移矩阵：

其余步骤与卡尔曼滤波相同，只需要提供状态向量初始值和估计方差矩阵初始值，然后指定两个噪声矩阵，还有观测向量，即可推算出k时刻的次优估计值^[11]。

5.实验设计与分析

5.1实验准备

实验需要三台手机开启热点提供WiFi信号，需要一部安卓系统为6.1以上的手机安装室内外无缝定位数据获取软件。

5.2数据采集

采集软件为com.collector.apk，1，1。此软件是安装在6.1以上安卓系统的手机，界面中的数据包括：陀螺仪三轴方向的数据，加速度三轴方向数据，周围各个WiFi的Mac地址，连接速度和RSSI值。

5.3数据处理

将三个手机作为AP，摆放在三个不同的位置，并建立坐标系，将Iphone1作为AP1，Iphone2作为AP2，Iphone3作为AP3，在建立的坐标系中，规定三个AP坐标：AP1（-2，4），AP2（2，2），AP3（1，-3）。起始方向为正北方向。一步步长为0.5m。

5.3.1WIFI坐标定位

（1）利用衰减模型计算目标距AP的距离

经过测试定位节点与参考节点之间的距离d=1m时，相对于三个AP的RSSI值分别为-40，-40，-42，即RSSI（0）=A分别为-40，-40，-42。模型公式为：

P_r（d）=RSSI=A-10·n·logd（5-1）

由于在比较开放的区域进行试验，所以n取2.1。

（2）利用最小二乘原理求解坐标

根据到三个AP的距离列立方程组，并转换为线性格式：

AX=b（5-2）

利用最小二乘原理求得：

X=（A^TA）^-1A^Tb（5-3）

5.3.2扩展卡尔曼滤波融合过程

（1） 计算状态向量预测值。公式为：

（2）计算观测向量预测值。此时观测向量预测值为WiFi定位坐标。

（3）利用泰勒公式一阶线性化状态方程求解状态转移矩阵。公式为：

（4）计算状态向量预测方差阵

P_k^-=φ_kP_k-1⁺φ_k+Q_k（5-6）

（5）计算卡尔曼增益

K_k=p_k/k-1H_k^T（H_kp_k/k-1H_k^T+R_k）^-1（5-7）

其中，量测方程中的H为单位矩阵。

（6）计算观测估计值

X_k=X_k/k-1+K_k（Z_k-Z_k/k-1）（5-8）

（7）计算下一时刻状态向量估计方差阵

P_k=（I-K_kH_k）P_k/k-1（5-9）

其中，I为单位矩阵，此时量测方程中的H也为单位矩阵。

融合后的所有坐标为P1（0.0956，3.9110），P2（1.0123，5.0291），P3（1.9675，4.0234），P4（3.0651，2.0861），P5（5.0112，0.0367），P6（3.0195，-1.9672），P7（2.0384，0.0764），P8（0.0098，-2.0946），P9（-1.9437，-2.4387），P10（-4.0541，1.0945），P11（-3.0712，3.1003），P12（-4.0497，5.0762）。

5.3.3数据可视化

通过MATLAB将实际行驶的坐标、WIFI的坐标和融合后的坐标绘制在坐标系中。结果如下：

图5.1真实行为轨迹，WiFi定位轨迹和PDR/WiFi融合定位轨迹图如图，红线是真实轨迹，蓝线是WiFi定位轨迹，明显可以看出已经和真实轨迹产生偏离，黑线为PDR/WiFi融合定位后的轨迹，对比发现融合后更接近真实轨迹。