基于排列码和AES的网络安全系统
作者: 刘永辉 刘 甜 于景利摘要:由于网络系统缺乏足够的安全性,从而阻碍了互联网络的发展。本文利用密码学的方法来解决网络数据传输的安全性问题,一种分组密码体制“排列码算法”和公开密钥密码体制的代表RSA算法。
关键词:网络安全;排列码算法; AES
中图分类号:F713.36 文献标识码:A 文章编号:1006-3315(2008)06-133-01
一、引言
随着金融电子化和无纸贸易的兴起,使得数据在网络中传输的安全性问题日益突出地显现出来。针对当今计算机网络在安全性方面的缺陷,人们提出了各种的方法来弥补,如访问控制系统、防火墙系统等。本文讨论的是将排列码和RSA用于网络数据保护的问题。
二、排列码加密算法
排列码从本质上说是一种分组密码,它满足分组密码的定义:
定义:分组密码就是一种满足下列条件的映射E: F2m×SK →F2m :对每个k∈SK,E是从 F2m到F2m的一个置换。
排列码算法采用排列运算,引入了路径的概念,形成了多对多映射的分组密码新概念。排列码算法与以往任何分组密码算法的不同点在于它在进行取非运算(即混乱运算)时也采用了路径加非的概念,从而极大的隐藏了真实密钥,并具备流密码的特性。其原理如下图所示。
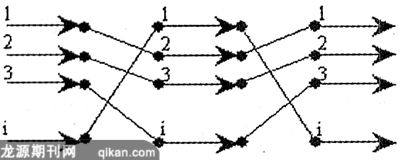
三、RSA算法
RSA系统使用两个密钥:加密密钥KE和解密密钥KD。二者分别用于公开域和私用域。RSA算法的基础是难以分解的大数素因子。
为了秘密数据通信,一个公开密钥密码算法要求必须不能有效地计算出KD (当然,也必须满足:D(E(X))=X)。除此之外,RSA还满足在解密之后继之以加密也能恢复原有信息X,亦即对D域中的所有X,有:E(D(X))=X。利用这个特性可以进行“数字签名”。由于以RSA算法为代表的公开密钥密码体制的提出,使得数字签名变得比较容易。
四、两种算法的异同
1.从处理效率看:前者是比较简单的比特处理形式,容易实现处理的硬件化(如今已经用硬件实现),利用软件也可实现高速处理。而后者则需要进行多倍字长运算,处理时间比排列码算法要长得多。
2.在密钥的分配和管理方面:前者必须对密钥进行秘密分配,密钥的定期更换很困难;而后者可采用公开形式分配加密密钥,并可像更换电话薄那样更换密钥。
3.在保密管理的密钥量方面:前者必须按通信对象保管不同的密钥,后者只需对自己的密钥进行保密管理。
总之,排列码算法具有密码使用简便及处理速度等优点;但在密钥的分配和保密管理方面存在问题;RSA算法则不需要秘密分配密钥,并且密钥的安全管理很容易,但缺点是处理速度慢。
五、混合加密方式
为了充分利用排列码和RSA两种算法的优点,而同时避免它们的缺点,提出了一种采用排列码和RSA的混合加密方式。采用这种排列码和RSA的混合加密方式传送明文数据P要经过以下几个步骤:
(1)发方制成密钥K,并从密钥服务器中获取收方公开的RSA方式的加密密钥KEb;
(2)发方用收方公开的RSA方式的加密密钥KEb对密钥K进行加密形成CK;
(3)发方用自己的RSA方式的解密密钥KDa对签名信息M(应包括收方自己的身份信息和日期时间)加密形成CM;
(4)发方用排列码密钥K对P和CM加密(即g(P+CM,K)),并加上CK形成密文C;
(5)收方使用RSA方式的解密密钥KDb对CK进行解密,取得DES方式的密钥K;
(6)收方用K解密(即P=g'(C-CK,K)- CM)得到明文P;
(7)收方从密钥服务器中获取发方公开的RSA方式的加密密钥KEa;
(8)收方用发方的RSA方式的解密密钥KEa由CM生成签名信息M(包括收方自己的身份信息和日期、时间);
(9)发方和收方均销去密钥K。
综上所述,排列码和RSA的混合加密方式兼有加、解密处理速度快的常规密码体制的优点和不需要进行密钥秘密分配且保密管理的密钥量也较少的公开密钥密码体制的优点,从而构成了一种较为理想的密码方式。
六、结束语
利用网络安全技术中的数据加密技术来实现重要数据的安全通信。本文借鉴加密技术中的两种密码体制的优点,采用混合加密体制,即采用一种新的分组加密算法一一排列码(武金木教授的专利)对明文加解密,三个会话密钥采用比较广泛的RSA算法加密来实现这种安全通信。
参考文献:
[1]Bruce Schneier, Applied Cryptography [M]. Beijing: China Machine Press, 2001.
[2]Tomasz Tyksinski, Foundations of differential cryptanalysis in Abelian Groups in information security, England, 2004.
[3]武金木,武优西,排列码加密解密方法及其排列码加密解密器,中国发明专利, CN99107969.8,2003,3。