构建有质量的小学数学计算教学

［摘  要］ 研究者结合“两、三位数除以一位数”的教学具体阐述构建有质量的计算教学的策略：重视经验唤醒，引导逐渐深入；关注实践操作，拓展理解空间；引导整合反思，提升运算能力。

［关键词］ 计算教学；实质策略；算理

一、提出问题

对于小学数学教学而言，计算教学占据着十分重要的地位，构建有质量的计算教学势在必行。当然，计算教学的最终走向是建构抽象算法模型，如何才能帮助小学生建构抽象算法模型呢？笔者认为，抽象的算法模型离不开形象的支撑，让学生亲历从动作操作到表象操作再到符号操作的过程可以帮助其实现算法抽象，从而真正意义上掌握算法、明晰算理。但在教学实践中，笔者发现部分教师在计算教学时会让学生机械模仿和反复操练来强化对算法模型的掌握。数学计算教学呼唤着一种有质量的深度探索，笔者以“两、三位数除以一位数（首位能整除）”的教学为例，谈谈如何构建有质量的计算教学，让学生体验计算法则的抽象，培养学生的运算能力，提高学生的数学核心素养。

二、教学过程简析

片段1

问题1：红红和芳芳一起团购了40支铅笔（即4捆），平均每人购买了多少支？

师：请列出算式并计算结果。（学生独立完成）

生1：40÷2=20。

师：具体说一说你是如何计算的？

生1：1捆为1个十，4捆就是4个十，将其均分为2份，也就是4个十除以2，得到2个十，因此40÷2=20。

问题2：先口算如下题组，然后比较每一组中两道题的相同点和不同点。

题组1：①90÷3；②900÷3。

题组2：①60÷2；②600÷2。

评析：认知心理学认为旧知是新知生长的基础，这为教师的教学提供了宝贵的教学资源。教师可以从学生已有的知识经验出发，基于学生的“最近发展区”准确设问，唤醒和打开学生的思维通道，使学生快速且兴趣盎然地进入课堂。正是有了教师的有效引导，才使学生在操作后自主回顾口算的算理与算法，为后续的深入探究做足准备。

片段2

（1）动手操作

问题3：独立思考后，列式并探索算法。

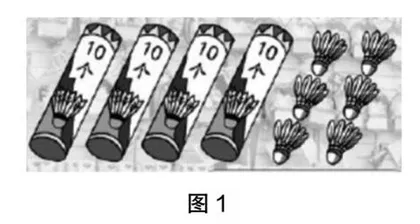
如图1所示，将羽毛球平均分给2个班，每个班分得多少个？

师：对于这个问题，我们是不是可以动手尝试？大家觉得可以怎么做呢？

生2：可以用小棒摆和分。

生3：可以直接在图上圈和分。

师：真是不错的方法呢！让我们一起试一试吧。（学生尝试，教师巡视）

师：谁愿意分享一下自己的方法呢？

生4：把它们看成小棒，先平均分这4捆小棒，再平均分剩下的6根小棒，最后合在一起，每个班23根小棒，也就是23个羽毛球。

生5：可以先平均分这4筒羽毛球，再平均分剩下的6个，最后合在一起，每个班可以分到23个羽毛球。

生6：我是按照数的组成计算的，先计算40÷2=20，再计算6÷2=3，最后计算20+3=23。

师：这三种方法有何共同之处？

生7：这三种方法都是先平均分4个十，再平均分6个一，最后进行合并。

评析：形象思维是抽象思维的源泉，算理对于小学生而言抽象难懂，有了实践操作的支撑，学生就可以较好地理解。这里，教师以问题情境为载体，以实践操作为方法，引导学生去思、去做、去说、去辩，从而获得对算理的直观理解，水到渠成地形成算法。

（2）表象操作

问题4：观察图2所示的算式与小棒，并在脑海中分一分、算一算。

追问1：试着说一说，你在246÷2时先分什么，再分什么，最后分什么？264÷2呢？（学生阐述，具体略）

追问2：分别说一说，两位数除以一位数、三位数除以一位数分别是先分什么，再分什么，最后分什么？

问题5：观察算式，想象与之对应的小棒图，并计算。

①26÷2；②28÷2；③482÷2；④693÷3。

追问：上述算式都是先算什么，再算什么？它们都是分几步计算的？

评析：表象思维是生成抽象思维的源泉，想要学生顺利抽象算法，除了动手操作的引导外，教师还要以有效的表象操作为指引，为学生积累丰富的表象思维，从而为后续抽象思维的形成提供有力支撑。学生在动手操作获取结果之后进行表象思维是实现算法抽象的重要一环，因此，教师要以问题为载体，设计拾级而上的活动帮助学生理解平均分的过程与步骤，自然地内化表象，助力抽象算法的形成。

（3）符号操作

问题6：独立思考并探索如何用竖式计算46÷2。

师：我们一起来看大家完成的情况。（教师呈现图3所示的典型竖式计算）

师：如图4所示，课本上展示的过程与步骤和你们的计算过程相比，这样列竖式有何好处？

生8：其实结果一眼就可以看出来，为什么还要这样一板一眼地进行烦琐的计算呢？

师：这个竖式中实则呈现了很多东西，谁能说一说它各个部分的含义及计算步骤？

生9：这个竖式是分两步计算的，也就是将46平均分成2份，首先……

问题7：根据图5中框的提示完成计算。（学生计算，教师巡视并指导）

问题8：试着列竖式计算246÷2，并在计算的过程中思考三位数除以一位数的计算步骤。

评析：理解符号的意义离不开符号操作过程，尽管竖式计算的步骤是硬性规定的，但也存在一定意义的支撑。这里，教师没有简单地将竖式输送给学生，而是引导学生自主探究、合作交流，以生成规范的竖式。正是学生经历了自主探究竖式、独立运用竖式、总结计算法则的一系列过程，才让竖式计算有理有据，才能获得更深层次的理解和认识。

片段3

问题9：在本节课中，计算方法是如何生成的？具体说说你的体会。（回放本节课中探究46÷2的过程）

评析：教师引导学生进行算法过程的回顾与反思，可以帮助学生积累充足的活动经验，自然积淀数学思想方法。这里，教师在课末组织学生回顾和反思，让学生在数学过程中感受算理与算法的一致性，感悟推理思想和建模思想，积累充足的活动经验。

三、教学思考

1. 重视经验唤醒，引导逐渐深入

学生都有主动思考的欲望，这是与生俱来的，他们总会自然地对自己喜闻乐见的事物进行思考与交流。所以，课堂上教师要重视唤醒学生的已有经验，以学生喜欢的、擅长的方式开课，顺其自然地将学生的思维引向深入，帮助他们一步步地探寻知识本质，抵达问题核心，让有质量的计算教学的构建成为可能。本课中，教师通过巧妙设计，紧紧抓住学生的已有知识和经验，引导他们逐渐深入地进行数学思考，这样的思考过程将更好地促进学生对计算本质的理解和认识，通过思维碰撞，不断产生思维火花，从而逐步形成对算理和算法的深刻理解。

2. 关注实践操作，拓展理解空间

小学生都是独具特点的生命个体，充分的实践操作能让学生的思维朝着纵深发展，最终无痕发展抽象思维能力。当然，想要形象思维朝着抽象思维自然过渡，就需要教师扎实、充分、有序地引导学生朝着高一级思维进阶，向着抽象算法模型进发。本课中，教师为了促进学生表征形式的自然转化，设计了动手操作、表象操作和符号操作等活动，引导学生在自主探究和合作学习的过程中探究与理解算理、抽象与理解算法，最终使教学目标顺利达成。

3. 引导整合反思，提升运算能力

学生只有对自己的活动进行反思，才能攀登高一级层次。因此，教师要引导学生经常对所学知识进行深度梳理与反思，促进学生能力的提升。本课中，教师以问题引导学生整理与反思，针对性地引导他们梳理做法与想法，使他们在深度交流中透彻理解算理与算法，自然地提升数学运算能力。