基于数学史的初中数学课堂德育功能初探

[摘  要] 数学史在中学数学课堂中具有重要的教育意义，其背后蕴涵丰富的、多元的德育内容素材. 研究者基于数学史的视角，以“二元一次方程组概念”为例进行教学设计，探析初中数学课堂教学中的德育功能，得出以下教学反思：滋润学生学习数学的“心田”;促进学生认识数学应用本质;弘扬中华优秀传统数学文化;渗透多元文化拓展学生视野.

[关键词] 数学史;初中数学课堂;德育;二元一次方程组

“立德树人”是当前教育的根本任务，如何在初中数学课堂教学中选取恰当的数学素材落实根本任务，是值得当前一线数学教师以及相关研究人员共同关注的问题.

已有研究发现[1]：将数学史融入初中数学课堂教学有利于德育目标的实现. 基于此，本文结合《义务教育数学课程标准（2022年版）》（以下简称《课标》）中课程目标的相关要求[2]，并基于数学史的视角以人教版二元一次方程组的概念为例探析数学史料中蕴涵的德育内容，发挥初中数学课堂德育功能的作用.

教学设计前期准备阶段

1. 教学对象认知结构分析

学生在小学以及七年级上册学习的基础上，可运用类比的方式探究、学习二元一次方程（组）及其解的概念.

2. 教学内容基本情况分析

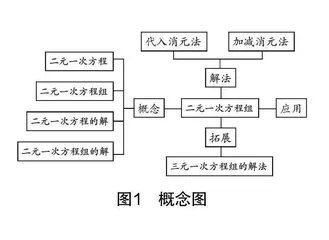
本节内容属于《课标》课程内容的“数与代数”学习领域，是人教版七年级下册第八章第一节的内容. 本节内容是对方程知识的再次探索与升华，是方程由“一元”过渡到“二元”的过程，对之后学习一次函数以及解决“多元”数学问题提供有利的工具. 全章知识结构的概念图如下所示（见图1）.

3. 基于数学史的文本分析

教材是进行教学的必备工具，对同一知识点的不同版本教材进行比较分析，是帮助教师对所教知识点进行有效备课的重要途径之一. 数学史料中具有丰富的德育内容素材，且本节内容具有大量的数学史料. 基于此，笔者选取全国使用率较高、影响较大的人教版、北师大版以及苏科版三个版本教材，对本节内容所在位置以及相关数学史料进行分析（见表1）.

由表1知：

从所在位置看，三个版本教材有所区别，对于本节内容，人教版和苏科版位于七年级下册，北师大版位于八年级上册. 其中，相较于人教版和北师大版，苏科版对本节内容是将二元一次方程与二元一次方程组及其解分为两节内容.

从相关数学史料看，三个版本均采用了我国古代数学著作《孙子算经》中的“鸡兔同笼”问题，其是对中华优秀传统数学文化传播的一种体现. 但侧重点有所不同，人教版仅是以文字的形式出现在习题中;北师大版和苏科版以图文并茂的形式出现在章前页，相较于人教版，更有利于激发学生的学习兴趣和动机. 此外，北师大版中的“老牛小马”问题改编自数学史上的“骡子和驴”问题，以图文并茂的形式出现在正文中;苏科版中选自《算法统宗》的“房客”问题以诗歌的形式出现在习题中，二者亦有利于激发学生的求知欲.

教学设计具体准备阶段

1. 教学目标

（1）理解二元一次方程（组）及其解的概念;能判断一组数是否是二元一次方程（组）的解.

（2）经历对数学史上以及日常生活中实际问题的分析、数学转化过程，培养学生归纳、概括的能力;为学生创设“数学—实际问题”的情境，让学生体会方程是解决实际问题的有效模型，初步培养数学抽象能力和模型观念的核心素养.

（3）在不同数学史料的融入过程中，让学生感受多元文化的熏陶;在中外经典数学名题的情境中，激发学生的好奇心和求知欲，让学生体会数学的应用价值;在小组合作辨析的过程中，初步培养学生理性、敢于质疑的良好品质.

2. 教学重难点

（1）重点：二元一次方程（组）的概念.

（2）难点：二元一次方程中含有未知数的项的次数均是1次;二元一次方程组中含有未知数的个数共有2个.

3. 教学过程

此部分结合当前教育理念、教学前期准备、教学目标以及教学重难点的确定，主要按照以下教学流程展开，如图2所示：

（1）创设情境，导入新知

此环节从3个情境问题展开，具体如下：

情境1  约公元四、五世纪，中国古代著名数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足. 鸡兔几何[3].”

问题1  在小学通过算术法以及七年级上册通过一元一次方程已解决过此类问题. 设：鸡有a只，请回顾列一元一次方程的步骤有哪些.

追问1  设：鸡有a只，兔有b只，你会得到怎样的方程？

追问2  一元一次方程的学习内容有哪些？

设计意图  以中国古代经典、有趣的“鸡兔同笼”问题为切入点，传播中华优秀传统数学文化，激发学生的学习兴趣;此外，引导学生回顾运用一元一次方程解决该实际问题的过程，并在已有2个等量关系中列出2个方程，引出本章的课题. 再次追问一元一次方程的学习内容，引导学生构建本章所学知识框架.

情境2  在数学史上有著名的“骡子与驴”问题[4]：骡子和驴驮着包裹行走在路上，已知骡子驮的包裹数比驴驮的包裹数多2个. 若骡子从驴那里拿来1个包裹之后，则骡子的包裹数恰好是驴的包裹数的2倍. 骡子和驴各驮有几个包裹？

问题2  设：骡子驮有m个包裹，驴驮有n个包裹，你会得到怎样的方程？

情境3  篮球联赛胜负问题（选自教材中的问题P87）

问题3  设胜x场，负y场，你又会得到怎样的方程？

设计意图  从多元文化的视角，促进学生感受方程思想，进一步体会学习二元一次方程的必要性;此外，充分利用教材中章前页的篮球联赛胜负问题，让学生再次体会学习二元一次方程是解决生活中实际问题的必要模型.

（2）概括共性，形成概念

此环节基于以上3个情境问题，引导学生观察、讨论、归纳，具体如下：

问题4  从方程的角度，这6个方程具有怎样的共同属性？

追问3  类比一元一次方程的学习，你能给这6个方程取名字、下定义吗？

设计意图  类比一元一次方程概念学习的探究思路，引导学生进行小组合作、讨论、观察，给新出现的方程取名字、下定义，得出二元一次方程的定义，进一步感知这两类方程的区别与联系，突出教学重点.

（3）辨析感悟，深化概念

此环节是在上一环节的基础上，引导学生辨析概念，具体如下：

活动1  请判断下列方程是否是二元一次方程，并给出理由.

（1）3x+y=7，

（2）x+y+z=5，

（3）x2+3y=9，

（4）+y=8，

（5）6a-13=b，

（6）2mn+n=6.

设计意图  通过小组交流、讨论，从正、反两方面强化学生对二元一次方程概念的理解. 设计不同类型的题目，总结在方程中等式两边均是整式，深度剖析含有未知数的项的次数是1次，而不是指未知数的次数为1次，进一步加强学生对二元一次方程概念中关键词的理解，突破第1个教学难点.

（4）续追促思，再成概念

此环节回到情境3，回到教材中，引导学生进一步得出相关概念，具体如下：

追问4  在篮球联赛问题所列出的2个方程中，x，y必须满足什么条件？

活动2  请判断下列方程组是否是二元一次方程组，并给出理由.

（1）2x+y=6，

x+3z=12. （2）3m+n=15，

mn=12.

（3）a=6，

b=8.            （4）6x+y=24，

x2+2y=3.

（5） 2x+y=6，

x=12.   （6）

+y=6，

6x+8y=32.

设计意图  在归纳、形成二元一次方程概念的基础上，回到教材中的篮球联赛问题，观察所列2个方程中x，y的意义，进而得出二元一次方程组的概念，再次突出教学重点;此外，通过活动交流、讨论，从正、反两方面强化学生对二元一次方程组概念中未知数的个数的理解，突破第2个教学难点.

探究  在情境3中，满足方程x+y=10，且符合实际意义的x，y的值有哪些？并把它们填入下列表中（回归教材中的探究问题）.

思考  上面哪一组x，y的值也满足方程2x+y=16？

活动3  动一动你聪明的大脑，编一道满足二元一次方程组x+2y=10，

2x+y=8 的应用题.

练习1  下列数组中是二元一次方程组x+2y=10，

2x+y=8 的解的是（    ）

A. x=2，

y=4. B. x=4，

y=8.

C. x=4，

y=2. D.x=8，

y=4.

设计意图  根据实际问题，引导学生小组讨论、探究并完成表格内容，得出二元一次方程（组）的解的概念;此外，给出一个开放题，让学生根据方程组内容自主编制应用题，体会二元一次方程组是解决实际问题的有效工具. 通过代入验证的方法判断一组数是否是二元一次方程组的解，并让学生解决自主编制的应用题，再次体会数学在实际生活中的应用价值.

（5）应用新知，巩固概念

此环节是在以上所有环节的基础上，选取中外历史名题感受二元一次方程组的应用价值，具体如下：

练习2  请独立列出对应的一元一次方程以及二元一次方程组.

（1）为鼓励孩子学好算术，父母决定：孩子每做对一道题奖励8元;每做错一道题罚款5元. 做完26道题后，谁也不用给谁钱. 问：孩子共做对、做错几道题？[5]（选编自：克拉维斯《代数》）

（2）昨日独看瓜，因事来家. 牧童盗去眼昏花. 信步庙东墙外过，听得争差. 十三俱分咱，十五增加. 每人十六少十八. 问：人瓜各几何？[6]（选编自：程大位《算法统宗》）

练习3  小组合作讨论，先列出对应二元一次方程组，并尝试列出对应一元一次方程.

（1）甲、乙两人各有钱若干. 甲若得到乙的，则有50;乙若得到甲的，则也有50元，问：甲和乙各有多少钱？[7]（选编自：《九章算术》）

（2）甲、乙两人各有钱若干. 若甲得到乙的7元，则甲的钱是乙的5倍多1;若乙得到甲的5元，则乙的钱是甲的7倍多2. 问：甲、乙各有多少钱？[8]（选编自：《计算之书》）

设计意图  再次从多元文化的视角设计习题，拓展学生的知识视野. 二元问题在历史上共分为4类，练习2属于1、2类问题，练习3属于3、4类问题. 对于练习2和练习3学生可通过一元一次方程来解决，并能列出对应的二元一次方程组. 其中，相较于练习2，练习3所列的一元一次方程结构较为复杂，通过比较，二元一次方程组结构简洁、明了，一方面体现了学习二元一次方程组的必要性;另一方面也为如何求二元一次方程组的解留下悬念. 总之，练习2和练习3的设计旨在起到承上启下的作用.

（6）课堂小结，升华概念

此环节旨在总结本节课所学内容，具体如下：