基于ADDIE模型的数学复习课单元教学设计思考

[摘  要] 基于ADDIE模型的数学复习课单元教学是对传统复习课的重构与革新. 为了适应素养本位下的数学教学变革，融合ADDIE模型，首先构建数学复习课单元教学设计的可行性及实施原则;接着以初三“方程”复习为例，呈现方程解法小单元复习的教学设计思路;最后得出三点教学思考：注重知识纵横梳理，整合学生知识体系;强调方法类比回顾，促使学生形成结构;追溯单元教学宗旨，培养学生素养精神.

[关键词] ADDIE模型，数学复习课，单元教学设计

引言

《义务教育数学课程标准（2022年版）》（以下简称“新课标”）指出：改变以课时为单位的教学设计，推进单元整体教学设计，加强知识间的内在关联，促进知识的结构化[1]. 新课标的颁布，无疑为知识本位向素养本位的转变指明了方向. 复习课作为促进学生知识系统化的一种有效教学模式，却被很多教师演变为一种“炒冷饭课”，单纯地将其理解为课时目标的简单合并与教材知识的机械回顾[2]，导致学生在面临纷繁杂乱的知识点复习之后，仍难以建立系统化、结构化的知识体系，这与当今素养本位指导下的教育理念相违背. 而单元教学设计作为连接宏观课程设计与微观课时设计的纽带，遵循ADDIE模型的实施步骤，超越课时主义的束缚，将碎片化、零散化的知识整体规划、系统实施，本质是促进学生所学知识趋向结构化，进而完善学生的认知结构体系，指向学生数学核心素养的发展.

另外，方程作为初中阶段数学知识体系的重要分支，不仅是中考的重要考查内容，也是学生描述数量平衡关系的关键模型. 为此，以ADDIE模型为基础，选取“方程”总复习内容进行初三数学复习课单元教学设计研究，并呈现方程解法的单元课时教学设计思路，希冀为初三一线数学教师进行复习课单元教学设计提供理论指导与实践参考.

基于ADDIE模型的数学复习课

单元教学设计原则

（一）ADDIE模型概述

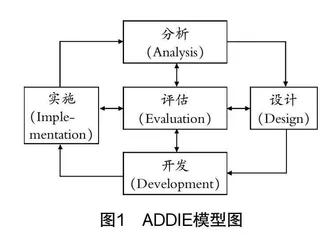
ADDIE模型中的5个字母代表不同的阶段，其应用时每个字母代表教学设计的不同环节，即字母A代表分析阶段，是对学习者、学习内容进行分析与确定;第一个字母D代表设计阶段，是对教学目标、教学活动、教学方法的设计;第二个字母D代表开发阶段，是对学习资源、学习活动、学习任务的开发;字母I代表实施阶段，是基于前面三个阶段的结果进行授课;字母E代表评估阶段，一般包括教学评价和教学反思. 具体如图1所示.

ADDIE模型的五个阶段并非孤立单一，而是互相关联、紧密联系的，外圈的箭头体现了该模型应用于教学设计时的实施逻辑顺序，内圈的双箭头指明了评估阶段与其他四个阶段间的关联作用.

（二）ADDIE模型应用于数学复习课单元教学设计的可行性

第一，ADDIE模型五个阶段的整体实施都是围绕学生“学什么”“怎么学”“如何判断学生学”的思路进行的，符合“以人为本”的教育理念，而复习课背景下的单元教学设计注重以数学知识复习路径为主线，促进学生建构知识体系，进而落实数学核心素养的培养. 可见，两者的理念相吻合，都强调“以人为本”的教育理念.

第二，ADDIE模型的五个阶段具有一定的整体性与动态性，彼此之间是相互联系、相互影响的，评估阶段并不是该模型的终止阶段，而是与其他四个阶段相关联并及时做出调整.而复习课背景下的单元教学设计不同于新授课的设计模式，更注重学生对数学单元知识的整体把握以及结构关联，更需要将评价贯穿于整个教学设计流程中，以便更大限度地发挥单元教学设计的实施效果.

第三，ADDIE模型的五个阶段遵循教学设计的实施步骤，“分析”阶段确定单元内容，“设计”与“开发”阶段制订单元教学设计，“实施”阶段开展教学实践，“评估”阶段对教与学进行评价反思[3]. 复习课背景下的单元教学设计需要确定单元复习内容、分析教学要素来明确单元复习目标，也需要教学流程的设计与实施促进学生回顾旧知，更需要及时的教学评价与反思来更新完善教学模式.

因此，基于ADDIE模型进行数学复习课单元教学设计是可行的，不仅符合“以人为本”的教育理念、整体动态的单元教学设计特点，而且也遵循单元教学设计的实施步骤，具备一定的科学性和可操作性.

（三）基于ADDIE模型的数学复习课单元教学设计实施原则

1. 梳理知识结构体系，理清复习课设计思路

徐章韬教授指出，知识梳理的内在本质是建立自然连贯、前后关联的知识序列;外部表象是知识脉络清晰化、结构体系可视化[4]. 知识结构梳理是复习课教学中不可或缺的重要流程，以ADDIE模型为基础进行数学复习课单元教学设计时，教师既要加强自身对单元知识整体框架、思想方法、素养指向的把握，又要注重教学过程中学生对单元知识多元化形式的梳理，促进学生认知结构的形成与发展.

2. 结合学生认知水平，合理筛选复习练习题

复习课教学不同于新授课教学，其价值除了温习旧知，更重要的是查漏补缺. 而复习题作为快速帮助学生摆脱薄弱知识困境的一种有效方式，是复习课教学中必不可少的辅助工具. 但是基于复习课背景下“以人为本”的单元教学设计理念，教师在设置复习题时，应当根据不同层次学生的认知水平，有针对性地安排复习题的难度和数量，围绕单元知识的结构特点设置基础性和拓展性题目，尽可能避免机械枯燥刷题、大量重复练题的复习教学弊端.

3. 聚焦数学核心素养，指向复习课教学初衷

史宁中教授强调，碎片化的数学知识无法清楚表述数学的本质，更难以凸显数学核心素养，应将知识内容前后整体设计，不仅要关注知识技能，而且要体现知识中氤氲的数学本质及数学思想，进而发展学生的数学核心素养[5]. 这种理念同样适用于复习课单元教学设计. 复习课背景下的单元教学核心并不是知识的逐点温习，而是在整体设计、结构复习的基础上促进学生知识的整体化、结构化、综合化，真正使数学核心素养的种子在学生身上生根发芽.

基于ADDIE模型的数学复习课

单元教学设计框架

钟启泉教授认为，单元设计遵循“ADDIE模型”[6]，吕世虎教授在此基础上，提出了单元教学设计的实施步骤[7]，具体如图2所示.

吕世虎教授呈现的单元教学设计实施步骤为单元教学的有效开展提供了可操作性的指引方向，但是结合教学阶段特点，复习课主要有日常的章末复习课和阶段模块复习课两种，此处主要聚焦初三阶段模块的复习课单元教学设计研究. 所以回归复习课教学的初衷，应当明确复习课并不是单纯的知识上的回顾，而是要促进学生能力的发展和素养的提升. 单元教学设计理念下的复习课教学更是要重视学生知识内容的梳理、认知网络的建立以及素养意识的形成.

因此，结合ADDIE模型的结构特点、吕世虎教授的实施框架以及复习课的教学初衷，可以得出如图3所示的设计框架.

（一）组建单元复习内容，明确单元教学核心

吕世虎教授认为，“单元”可以是基于教材编排视角形成的教材中已有章节单元，也可以是根据教学实际需求在知识内容结构上重组而形成的单元[8]. 章飞教授也指出，“单元”的大小无固定划分模式，可依据学生的学习状况和认知水平灵活组建[9]. 因此，这也在一定程度上凸显了组建单元内容的灵活性和生本性. 例如：围绕初中苏教版数学教材“初中方程”这一核心概念，发现初中阶段教材中的一元一次方程、二元一次方程（组）、分式方程以及一元二次方程大都按照“概念—解法—应用”的环节进行设置，因此可以将上述四类方程进行整合形成单元内容，按照先复习概念，后复习解法，最后实践应用的教学路线进行复习.

（二）分析单元教学要素，整体把握知识结构

单元教学要素分析并不是教学设计的形式化复制，而是为后续单元教学目标的确定提供完备的教学依据. 首先，学科分析主要把握单元复习内容在整个学科前后知识的定位以及与中考的承接;其次，课标分析与教材分析重在明确单元复习内容的宏观教学要求和编排实施方式;再次，学情分析既要把握学生现有的认知基础，又要结合本单元内容分析学生应当具备的认知基础，这两层次认知基础之间的差距就是学情分析应当突破的核心问题[10];最后，教学重难点分析为复习课单元教学需突破的关键点提供了指引方向.

（三）确定单元教学目标，指向知识复习目的

单元教学目标统摄单元课时教学目标，并不是单元各课时教学目标的简单合并[11]，前者与后者是整体与局部的关系. 例如：根据方程单元内容的复习路径（概念—解法—应用），可以将单元教学统领下的方程知识复习划分为三个小单元，不仅可以明确单元教学目标，而且有助于凸显方程的复习路线，具体如图4所示.

（四）开展单元复习教学，贯彻知识复习理念

富含中观性的单元教学设计上连宏观课程目标，下接微观课时目标，因此单元教学目标的达成最终要通过课时教学来落实[12]. 传统课时主义下的复习课教学倾向于知识的温习与题目的练习，而基于ADDIE模型的复习课单元课时教学强调以复习路径为基准，在注重梳理、巩固已学知识方法的基础上凸显学科本质规律，帮助学生建构数学知识思想方法体系，增进学生对知识的再认识、再实践、再创造，避免学生知识复习的零散化、碎片化，指向知识复习的结构化、系统化、深度化，进而提升学生能力，培养学生核心素养.

（五）复习教学评价反思，完善单元设计模式

鲍建生教授提倡，教学与反思是一个持续改进的循环过程，教师需要专业反思但不能止于反思[13]. 复习阶段的单元教学更需要教师敢于反思、善于反思，并及时对学生进行过程性评价和总结性评价，为复习单元教学设计整个流程的完善提供事实依据. 单元教学理念指导下的教学评价与反思，更要注重评价主体的多元化和反思形式的多样化，最大限度地发挥单元教学设计在模块复习阶段教与学的价值.

基于ADDIE模型的数学复习课

单元教学设计应用

由于篇幅限制，只呈现“小单元二方程解法复习”的设计思路，希冀为一线数学教师进行知识复习单元教学起到抛砖引玉的作用. 具体设计思路如下：

（一）单元二教学目标

1. 系统梳理和回顾一元一次方程、二元一次方程（组）、一元二次方程、分式方程的相关解法及其步骤，掌握不同方程的解法以及解方程的一般思路;

2. 在整理四类方程解法的过程中，明晰解方程中蕴含的“转化”数学思想以及“消元”“降次”方法，通过归纳总结、合作交流体会解方程的本质内涵，培养自主探究、归纳概括的数学能力;

3. 深刻领会从“特殊到一般”的方程解法探究思路，类比迁移少元低次方程的解法，明晰多元高次方程的解法思路.

（二）单元二教学重难点

教学重点：掌握不同方程的解法，归纳四类方程的解法步骤，类比迁移形成方程解法思路.

教学难点：对不同方程解法的运用以及注意事项.

（三）单元二教学过程

1.  开门见山，导入旧知

【问题1】 同学们，上节课我们复习了方程的相关概念，知道了不同方程的区别与联系以及“元”“次”之间的关系，同学们能快速列举一些方程吗？它们属于哪类方程？

【学生活动】 学生列举出不同方程，并顺利说出方程的类型.

同学们列举的这些方程该如何去解呢？我们会用到哪些方法呢？那么这节课我们就来复习不同方程的解法.

【设计意图】 从方程种类引入解法，帮助学生明确所复习的关键内容，触碰学生头脑中原有的数学方程知识网络，使学生回忆不同方程解法的相关知识，为后续教学做铺垫.

2. 梳理旧知，回归基础

【问题2】 初中阶段我们学习的这些方程该如何求解呢？这些解法的步骤是什么？请同学们同桌两人进行交流.