基于物理情境的九年级学生科学思维测试工具编制及验证

摘要：科学思维是2022版新课程标准中核心素养的重要组成部分。为评估九年级学生的科学思维能力，特设计了一套测评工具，并基于Rasch模型从评分者信度、单维性、试题评分结构、试题拟合度、分离度、误差统计、怀特图等方面评估工具的整体质量。经分析，测评工具整体信效度较高，试题拟合度和分离度符合要求，误差在可接受范围内。怀特图的分析结果显示，学生们的科学思维水平普遍有待提高。总体上看，这套测评工具符合要求，可信度比较强。基于Rasch模型的测试质量分析也为进一步优化测试工具提供了参考。

关键词：科学思维；质量分析；九年级学生；Rasch模型

中图分类号：G62 文献标识码：A 文章编号：1005-4634（2024）04-0010-07

以科学思维为导向的科学教育改革受到了西方国家的高度关注，美国于2013年颁布《新一代科学课程标准》（Next Generation Science Standards，简称NGSS） [1]，明确提出科学思维导向的课程与教学目标，确定了批判性思维、计算思维、比例推理、定性和定量思维等8种思维能力。我国《义务教育物理课程标准（2022年版）》（以下简称22版物理新课标）指向核心素养，其重要组成部分即科学思维，并聚焦于科学高阶思维，涉及科学推理、科学论证、模型建构、质疑创新等能力 [2]，强调通过科学观察、实验探究、推理计算等方法，培养学生的物理观念、科学思维以及科学态度与责任等核心素养。其中，科学思维主要涵盖模型建构、科学推理、科学论证、质疑创新等要素，是从物理学视角对客观事物的本质属性、内在规律及相互关系进行认识的方式，是客观事物本质属性的反映，是一种认识世界的方法。22版物理新课标强调运用分析综合、推理论证等科学方法，基于事实证据和科学推理进行论证、批判和反驳，进而提出创造性见解，以提高学生科学创新能力、科学实践能力和培养科学思维习惯 [2]。由此可见，国内外课程标准均强调科学思维培育，在国际测评中，我国中学生虽然屡次在数学和科学方面取得出色的成绩，但是诸如科学推理、协作式问题解决能力等却没有表现出优势，且STEM职业期望不容乐观。事实上，科学思维能力需要从小培养，学龄前儿童就已展现出识别和测试因果关系的基础能力 [3]，但这些潜力的充分发挥仍需依靠学校的专门课程和系统化教学 [4]。为了持续并有效地提升学生的科学思维能力，需要通过科学化的测试来定期评估他们的进展，从而及时调整和优化课程结构与教学方式。值得注意的是，科学思维测评在国际上已被视为关键评估领域，但当前我国仍缺乏与新课程标准紧密契合的科学思维测评工具。

2022版物理新课标中的科学思维是指一种高阶能力，不仅包括严密的科学推理过程，还需要科学论证进行推论，从而加工处理以表征建模的能力，需要一套严密的逻辑体系 [2]。正是由于这种能力的复杂性，很难直接去考察和测量，需要通过真实情境下的任务题来考察。低年龄段儿童的阅读理解和写作能力较弱，不宜采用纸笔的书面方式进行，以免影响结果的真实性。国际学生测评项目（Programme for International Student Assessment， 简称PISA）的测试对象是15岁学生，在我国正好对应为九年级，该学段学生的认知能力处于形式运算阶段，思维的可逆性、灵活性和逻辑思维能力均得到快速发展，也是科学思维培养的黄金期。因此，本研究聚焦于科学思维发展的关键阶段——九年级学生，将其作为测评对象。鉴于学科内容导向的科学思维测评工具更符合我国的教学情境和学习文化，本研究开发了基于物理情境的纸笔测试任务题来评估学生的科学思维能力，并对此测评工具进行了Rasch模型的检验，旨在准确测量我国典型地区九年级学生的科学思维水平。最后，对试题的合理性进行了验证，以确保评估的准确性和有效性。

1研究方法

1.1研究工具

本任务题共有3道大题，每道题分别设置2～3个小问 ，均为简答论述题。第一题的第一小问主要考察了串联电路电流相等，额定电压相同时额定功率大电阻小、实际功率大的相关电学知识，考察学生科学推理能力中提出问题与做出假设、解释数据与生成结论维度，科学论证能力中观点、事实证据与理论基础和推理与反驳维度；第二小问主要考察了并联电路电压相等、并联电路与串联电路的识别与使用的相关电学知识，考察了学生科学推理能力中的设计实验与生成证据维度，科学建模能力中的模型建构与使用、模型比较、修正与检验、建模元认知与元建模维度。第二题的第一小问和第二小问主要考察了电路模型中各个元件的用途、滑动变阻器和定值电阻的作用、串联电路分压原理的相关电学知识，考察学生科学建模能力中的模型建构与使用、模型比较、修正与检验、建模元认知与元建模维度。第三小问主要考察了电路中外接法与内接法误差产生的原因、电流表和电压表的阻值和伏安特性曲线的相关电学知识，考察了学生科学推理能力中提出问题与作出假设、设计实验与生成证据、解释数据与生成结论维度，科学论证能力中观点、事实证据与理论基础和推理与反驳维度。第三题的第一小问主要考察了影响导线电阻大小的因素、电路干路导线粗的原因、并联电路中干路电流是支流电流之和/干路电流大于支路电流、焦耳定律和欧姆定律的相关电学知识，考察学生科学推理能力中提出问题与做出假设、解释数据与生成结论维度，科学论证能力中观点、事实证据与理论基础和推理与反驳维度；第二小问主要考察了构建正确的电路模型、并联电路各支路间电压相等，各支路用电器相互独立/互不影响的相关电学知识，考察了学生科学推理能力中设计实验与生成证据维度，科学建模能力中模型建构与使用、模型比较、修正与检验、建模元认知与元建模维度。计分方式按照回答踩分点将等级划分为水平0、水平1、水平2，共计得分点17个；该测试满分为54分，测试时长为40分钟。总体而言，测试项目的综合能力要求符合科学思维的内容水平。

1.2研究对象

本次测试对象为九年级学生，抽取了北京、上海、浙江和山东主要行政区的中等偏上的学校，并且对各个地区学校的有效男女人数进行了统计，男生人数总计642人，女生为789人。原始测试卷共收集到1 390份，经过人工筛选剔除份无效问卷71份，最终保留1 319份有效数据，有效率达95%。共有4位评分员进行主观评分。首轮根据制定的量规进行100份问卷的评定，计算两两之间的一致性，并且组织讨论不一致的地方，打磨量规再次评分，直至达到80%以上的一致率。第二轮继续抽取100份问卷，同第一轮步骤再次进行评分。第三轮继续抽取100份问卷，持续磨合量规并进行评分，计算评分一致性，并在一次评定达到80%的一致性后进行独立评定。最后进行抽评，抽评的方法也是由两两交叉进行抽评，抽取有效数据的20%，且其一致性均达到0.8以上，并再次进行校对统一得到最终的有效数据。

1.3Rasch模型测量原理

Rasch模型主要分析被试者能力水平与测验项目之间的关系，常将学生能力与项目难度放在同一标尺上比较，对于能力型任务题质量的检测具有广泛的适用性 [5]。其在能力测评工具开发方面具有3个显著优势：第一，该模型可以将非线性数据转化为等距离特征的线性数据，使得数据之间的差异具备客观性与可比性；第二，Rasch模型可以将被试和项目放在同一个标准上进行测量，这时项目难度和学生水平就可以进行比较；第三，Rasch模型测量的被试能力和项目难度水平具有独立性，不受样本和项目变化的影响 [6]。项目反应理论讨论被试的能力水平与测验项目，克服了经典测量理论中的样本依赖问题，能够使测试过程更加稳定和客观 [7]。

2数据分析

2.1描述性统计与分布检验

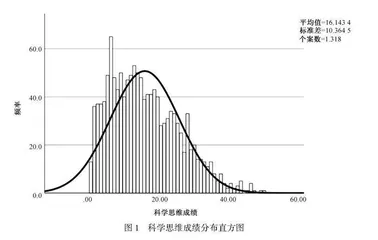
为明晰科学思维的表现，计算其极大值、极小值、平均值、标准差、方差、偏度和峰度。结果显示，1 319名学生的平均分为16.143 4，最大值为52分，最小值为2分，标准误为0.067，方差为107.423。 由此可见，学生能力差距较大，各地区学生差距也较为明显。合格的测评工具测得的结果应该是呈正态分布的，测试难易合适，即得高分和低分的学生较少，本测试检验结果如图1所示，学生科学思维的成绩整体呈正态分布。其中，得分在7～20分的人数最多；高分数段的人数偏少，低分数段的人数偏多，说明题目对学生而言比较难，学生科学思维能力水平不佳。

为进一步呈现成绩分布特征，做出科学思维累积率（图2）和趋势累积率（图3）示意图，前者的预计累计率用纵坐标表示，后者的实测累计率用横坐标表示，两者相等时测试结果呈正态分布，图像应该是一条直线。另外，在趋势图中，如果数据呈正态分布，那么数据点应该均匀分布在Y=0的直线两侧 [8]。从图2可见，实测累计概率与预计累计概率比较接近，因此可以认为科学思维成绩是正态分布的。这个结果也说明测试项目的区分度较好，结合表1数据，偏态系数为0.625，表明学生成绩呈正偏态，即低分学生比较多，这个结果与图3呈现一致。峰态系数为-0.136，接近0，分布峰的形状较正态分布更平、分布现状相对矮胖，基本呈现正态分布。

2.2测试信效度

本研究运用SPSS26.0分析该数据的信效度水平。通过Kappa系数考查人工评分者的一致性，以确定评分者信度。当Kappa值介于0.75～1时， 较高程度的评分者之间具有一致性 [9]。人工[HJ59x]评分步骤如上文所述，最终达到总体项目的一致性信度为0.921。说明此测评工具的人工评分信度是可靠的，该测试项目信度良好。通过Winsetps 3.81.0导入了1 319个观测值数据，对全部27个评价项目进行估算。并从以下5方面统计整体工具质量，即平均难度估计值（measure）、数据与模型拟合指数（infit与outfit）、误差（error）、信度（reliability）和分离度（seperation），具体结果见表1。学生的measure为-1.26，说明测试项目整体对被试偏难，但测试项目的measure值为0，说明试题难度处于中等水平，评价项目较好地拟合了被试的能力水平，适合该样本的评估。items separation为试卷的分离度，数值为10.10>2，说明该试题分离度好，items reliability的值为0.99，说明信度很好。infit与outfit是否拟合主要是看两者之间的值，理想值为1，0.5～1.5之间属于可接受范围 [10]。items infit MNSQ为1.01，items outfit MNSQ为0.99，接近理想值，这说明测试项目整体的拟合度较好。 

项目单维性分析假设每个评价项目都在同一潜在特质上被测量 [11]，即被试在项目中的回答仅源自潜在特质或能力，其他因素不起作用 [12]。一般使用主成分分析方法来测查项目单维性，标准残差对比图通常表明项目难度估计值与评价项目载荷系数之间的关系 [7]。评价项目共计27个，分别用图4的大小写字母（A、a）表示，纵坐标是项目载荷系数，横坐标是项目难度，理想区间为-0.4～+0.4，超出该范围的，则认为不满足单维性要求 [13]。图4中所有项目的载荷系数均在-0.4～+0.4之间，因此本研究开发的测评工具单维性较好。

图5展示了试题评分等级结构的分析结果。图中的纵坐标（probaility of response）表示被试者得分为0、1和2的概率，横坐标（person [minus] item measure）表示被试者能力与项目难度值之间的差异。在曲线交叉的地方即阈值（threshold）位置，对应的纵坐标表示被试者获得两种分数的概率相同。试题每个维度的评分等级类别曲线都有明显的峰且平直，并且在横坐标覆盖一定的范围，表现良好。