《几何画板》在初中数学教学中的应用与实践

摘要：几何画板因为易操作且绘图及动画功能强大，渐渐被广泛使用。它的直观性和生动性可激发学生的学习兴趣，让学生可以更直观地理解数学概念、发现几何图形及函数图象的特征和性质，培养他们的形象思维能力及自主探究能力。几何画板在初中数学教学中的应用可提高教学效率，激发学生的数学学习潜力，为将来的学习打下基础。以下我将分享《几何画板》在数学教学中的应用的几点尝试。

关键词：初中数学；几何画板；教学实践；

一、几何画板在初中数学教学中的应用具有以下优势：

1. 提高学生的学习兴趣和积极性：通过几何画板作动图，能使学生能够更加生动形象地理解抽象的数学概念和性质，从而激发其学习的兴趣和积极性。

2. 提高学生的学习效率：通过几何画板绘制图形，提升空间想象力，使学生学习更高效。

3. 提高学生的解题能力：通过几何画板绘制复杂的动图，锻炼学生的思维能力，并通过观察，找出解题思路。

二 、《几何画板》在数学教学运用的一些实践探索

（一）利用《几何画板》进行数学定理的验证

例：三角形内角和定理

用《几何画板》软件画任意一个三角形，“度量”它的各个内角并”计算“它们的和，然后拖动顶点改变所画三角形的形状，再“度量”变化后的各内角并“计算”内角和．让学生直观感受三角形内角和始终等于一个定值——180°。

（二）利用《几何画板》增强空间想象力，使抽象问题形象化

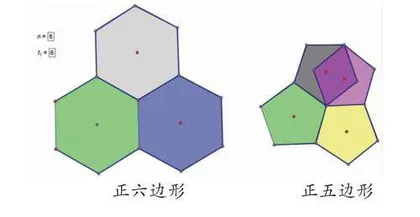
例一：探索正多边形平面镶嵌问题

利用几何画板，先画出一个正多边形，以一边为轴利用“变换”中的“反射”功能，画出该正多边形轴对称图形，再选两个图形有公共顶点的一边，重复以一边为轴利用“变换”中的“反射”功能画出该正多边形轴对称图形这一操作，直到所画对称图形相切或者相交便停止。接着“构造”正多边形“内部”，填充颜色，便可直观地看出该正多边形是否能平面镶嵌并帮助学生总结出正多边形能平面镶嵌的一般规律。

例二：一次函数 的平移性质

打开几何画板，点击“数据”，选择“新建参数”，将参数名称改为“b”，点击“绘图”，选择“绘制新函数”，点击“方程”选择“y”，一次点击“=”“ ”“+”“b=1.00”“确定”，就可显示函数 的图象。接着右击“b=1.00”，选择属性，选择参数，选择范围“-10到10”，点击“完成”，再左击选择中“b=1.00”，点击菜单左上角的编辑，选中“操作按钮”再选择“动画”。学生可直观观察，当b变大时，一次函数的图象向上平移，当b变小时，图象向下平移。

（三）利用《几何画板》辅助教师讲授基础知识，帮助学生理解基本概念

例：一次函数与图象

动态反映，把抽象变为具体，以课堂演示 这条直线的形成为例．打开《几何画板》，建立坐标系，先在x轴上取点A，度量该点的横坐标，然后利用“度量”菜单中的“计算”功能计算出2x，“度量”菜单下的“绘制点”绘出点B（x，2x），最后将点B设置为“显示”菜单下的“追踪绘制的点”．

引导学生发现点B是满足 函数关系的点。提问：1、这样的点有多少个？2、这样的点有什么特点？学生通过观察几何画板，较易得出满足该关系式的点有无数个，且都在一条直线上这一结论。这一过程让同学们形成函数图象的概念。

三、利用《几何画板》在变化中寻求特殊，发现解题的思路．

例题：有一架竖直靠在直角墙角的梯子正在下滑，一只猫紧盯住梯子正中间的老鼠，等待与老鼠距离最小式捕捉，把墙面、梯子、猫和老鼠都理想化为同一平面内的线和点，模型如图， ，点 、 分别在射线 ， 上， 的长度始终保持不变， ， 为 的中点，点 到 ， 的距离分别为4和2，在此滑动过程中，猫和老鼠的距离DE的最小值为。

打开几何画板，画射线BA，BC，构造射线BC上一点G，以G为圆心构造半径长为4圆，交射线BA于点M，构造线段MG的中点E，连接BE，DE.度量线段MG，EB，ED的长度，拖动点“G”在射线BC上运动，点M跟随着在射线BA上运动，但线段MG长度始终不变，通过拖动点G，学生观察到线段BE=2不变，当线段DE取得最小值时，三点B，E，D看起来共线。三点共线时，怎么求线段DE的长度？为什么三点共线时，线段DE最短？通过动图，学生能更直观地思考问题。最后将问题转化为“最短路径”问题。

四、总结

《几何画板》的应用使课堂教学更加地生动和形象，激发学生的学习兴趣，提高学生的空间想象力和数学学习能力，且其具有简单易操作性，相信广泛推广对中学数学的学习质量的提升是具有帮助性。

参考文献

[1] 汤文卿新课标理念下的中学数学课堂教学[M] 中学数学教育， 2004年第3期

[2] 教育部．《义务教育数学课程标准》（2011年版）[M] 北京：北京师范大学出版社，2011.6

[3] 林君芬 余胜泉信息技术与数学教学整合的教学模式研究 [D] 北京：北京师范大学现代教育技术研究所，2005.7