基于深度置信网络的轨道交通车辆轴承故障诊断研究

摘要：针对城市轨道交通车辆轴承在列车运行过程中受到强噪声污染，导致振动信号不稳定、特征提取难度大，提出了基于深度置信网络的轨道交通车辆轴承故障诊断方法。首先，对故障信号的统计样本参数等典型信息进行时域特征提取。其次，通过对每层的RBM训练的方法来确定参数θ最优取值，并自动提取信号的深层特征。最后，将提取的特征输入DBN模型进行分类识别，从而完成故障类型分类。

关键词：车辆轴承；故障诊断；时域特征；RBM；DBN模型

中图分类号：TP311  文献标识码：A

文章编号：1009-3044（2023）26-0092-03

开放科学（资源服务）标识码（OSID） ：<G：＼飞翔打包文件一＼电脑2023年第二十六期打包文件＼6.05xs202326＼Image＼image1.jpeg>

0 引言

城市轨道交通车辆的实际承载能力主要依靠转向架[1]。轨道交通车辆的转向架轴承往往容易发生故障，一旦故障，整组机车的安全性将受到严重影响[2]。轴承作为转向架核心机械部件，其健康状况直接影响转向架的安全性和有效性。使用准确、高效的故障诊断技术可减少转向架维护成本、提升转向架稳定性，进而为轨道交通车辆运行安全提供保障。所以，对城市轨道交通转向架轴承的故障诊断越来越受到人们的关注。

近年来，诸多专家学者通过时域、频域、时频域等单一特征来凸显故障信息，并通过分类模型对故障进行分类。文献[3]提出了一种基于混合域特征处理的方法。但混合域特征集具有维数高、计算复杂等特点，会严重影响故障诊断的准确性。针对混合域特征存在的缺陷，文献[4]使用局部线性嵌入（LLE） 算法来寻找被高维特征所暗含低维流形结构，使降维特征保留原始拓扑结构。但在降维之后，数据的总体分布将在低维空间中易失真。文献[5]提出主成分分析法（PCA） ，通过提取特征的协方差矩阵来降低维数，但PCA偏向于全局重建信息，忽略了数据和样本之间的相关性。文献[6]通过优化支持向量机法对故障类型进行分类，进而完成故障诊断。文献[7]利用麻雀搜索算法在支持向量机对于电机故障的分类的模型上进行惩罚参数和核参数的挑选和模拟，选择最合适的参数组合建立SSA-SVM故障诊断模型，进而完成故障诊断。上述基于机器学习的故障诊断识别方法，虽然有效识别故障类型但存在输出不够稳定、故障识别精度低等问题。

本文提出一种基于深度置信网络的轨道交通车辆轴承故障诊断方法。首先，在时域中提取故障信号的统计样本参数等典型信息。其次，通过对每层的RBM的训练的方法来确定参数θ最优取值，并自动提取信号的深层特征。最后，RBM提取的特征被发送到分类器Soft-max，结合故障类别标签，从而完成故障类型分类。

1 时域特征基本理论

时域信息用于描述以时间为变量的信号波形[8]。时域信号包括量纲特征参数以及无量纲特征参数。时域特征提取通常包括的参数较多（比如RMS、峭度、裕度、歪度、均值等），具体计算公式见参考文献[9]。

2 深度置信网络

深度置信网络（DBN） 主要由无监督预训练部分（多层受限玻尔兹曼机（Restricted Boltzmann machine，RBM）） [10]和有监督反向微调部分（BP 神经网络）等两部分组成。在预训练部分，DBN利用逐层贪婪学习法训练RBM的每一层，并将前一层的隐藏层输出用作下一层的显式层输入。在反向微调部分，使用监督学习来训练BP网络，并将实际输出和标签之间的误差逐层向后传递，以微调DBN每层中节点的权重和偏差。

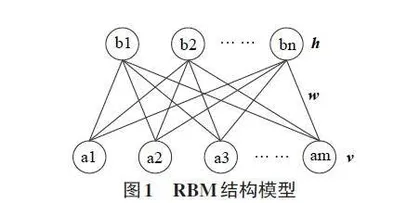
RBM由显层v和隐层h组成，显层和隐层皆是无连接层内节点，层间节点由权值w全连接，其结构模型如图1所示。RBM是一个基于能量的模型，对于（ v，h） ，假设其神经元都是二值状态，即只有激活和未激活，用1和0表示。能量函数如下：

[Eθ（v，h）=-i=1maivi-j=1nbjhj-i=1mj=1nviwijhj]

式中： m和n分别表示显层和隐层节点数目，[vi]表示第i个显层节点的二值状态，[hj]表示第j个隐层节点的二值状态，[ai]表示第i个显层节点的偏置和[bj]表示第j个隐层节点的偏置，[wij]表示第i个显层节点和第j个隐层节点的连接权值。

基于能量函数得到显层和隐藏的联合概率分布：

[p（v，h）=1Zv，he-E（v，h）]

式中： Z为配分函数，即一个归一化函数。进一步推导得出显层和隐层节点的激活函数：

[P（hj=1）=vhe-E（v，h）he-E（v，h）=σ（bj+iviwij）]

[P（vj=1）=vhe-E（v，h）ve-E（v，h）=σ（ai+jhjwij）]

式中： σ 为 sigmoid 函数。

[σ（x）=11+e-x]

为了得到模型的最优解，定义似然函数：

[L=i=1mlnP（vi）]

利用随机梯度上升法求极大似然函数的解，令 θ = （ a，b，w） ，有：

[-∂lnP（v）∂θ=v，hP（v，h）∂E（v，h）∂θ-hP（h|v）∂E（v，h）∂θ=∂Edata（v，h）∂θ-∂Emodel（v，h）∂θ]

Hinton [11]等基于极大似然估计提出了对比散度法 （ contrastive divergence，CD）来更新参数：

[∇wij=α∂lnP（v）∂wij≈α（P（hj=1 | v（0））v（0）-P（hj=1 | v（k））v（k））]

[∇ai=α∂lnP（v）∂ai≈α（v（0）-v（k））]

[∇bi=α∂lnP（v）∂bj≈α（P（hj=1 | v（0））-P（hj=1 | v（k）））]

式中： α为学习率; v（ k）表示k步CD算法后显层节点状态，一般情况下取k = 1。RBM训练流程如图2所示。

3 故障诊断方法

本文所研究方法为一种基于时域特征和深度置信网络（DBN） 的故障信号识别方法。具体流程如图3所示。

首先：对故障信号进行时域特征提取（如峭度、裕度、脉冲因数、波形因数、波峰因数等参数）。

其次：建立了基于RBM的DBN模型，以解决传统方法中的梯度分散和局部优化问题。DBN模型的具体训练及故障分类步骤如下：

1） 明确故障类型（输出节点数），将标准化的数据划分为训练和测试两类数据集。

2） 初始化DBN模型，设置层数、节点数、学习率等参数。

3） 将训练数据集输入第一层RBM，完成无监督训练。第一层充分训练后的隐层作为第二层RBN显层开始训练第二层，同理往下，可训练并计算出每层RBM 的局部最优参数（获得最优模型）。

4） 由BP层从上到下对RBM的每一层进行微调，并逐层调整RBM的权重参数，使其收敛到全局最优（DBN训练曲线图见图4） 。

5） 重复3） 和4） ，完成设定的迭代次数后停止训练，获得DBN故障分类模型。

6） 将测试数据集输入已经完成训练的DBN模型进行分类识别。

最后：为了提高分类效果，对整个网络的权重进行微调，并使用微调后的网络实现最终分类。

4 实验与分析

实验采用美国凯斯西储大学电气工程实验室数据[12]，其中轴承型号为 6205-2RS JEM SKF，负载2.237 kW，转频1730 r·min－1，采样频率为 48 kHz。为模拟轴承损伤故障，对其各部位增加裂纹，裂纹直径 0.1778 mm，裂纹深0.2794 mm。随机选取轴承外圈的一组数据（采样频率为12 kHz，采样点数为1200） ，选取正常信号、内圈故障、外圈故障、滚动体故障等4种状态下各60组样本数据，采用本文所提方法处理轴承数据，并进行分析。

4.1 实验分析

首先对故障信号的统计样本参数等典型信息进行时域特征提取。图5展示了4种不同健康条件下轴承的振动信号。可以看出，轴承的健康程度不同，振动信号波形的幅值也不相同，并且波形的特征也不相同。通常来讲，当轴承出现磨损以后，振动信号的峰峰值幅值有效值，以及峭度值都会增大。

其次，通过训练每层的RBM来确定参数θ最优取值，并自动提取信号的深层特征，将所提特征输DBN模型进行分类识别，从而完成故障类型分类。实验结果（见图6） 表明，本文所提方法能够准确识别故障类型。

4.2 对比实验

为表明本文方法的优越性，与SSO-SVM[6]、SSA-SVM[7]、PSO-SVM等方法进行对比。结果（见表1） 验证了本文所提方法在故障类型识别准确率方面明显优于其他几组模型。

为了防止偶然事件的干扰， 对DBN法分类与PSO-SVM法分类分别进行 10 次实验，取十次结果均值进行对比，实验结果见表 2 所示。DBN平均分类时间为16.42503s， PSO-SVM平均分类时间为20.49177s，DBN平均识别速度要比PSO-SVM平均识别速度快4.06674s。DBN故障识别平均正确率为100%，PSO-SVM故障识别平均正确率为98%（在第1、3、8、10次的故障识别正确率如图7所示，为95%） 。

5 结论

本文提出了基于深度置信网络的轨道交通车辆轴承故障诊断方法。首先，对故障信号的统计样本参数等典型信息进行时域特征提取。其次，通过对每层的RBM训练的方法来确定参数θ最优取值，并自动提取信号的深层特征。最后，将提取的特征输DBN模型进行分类识别，从而完成故障类型分类。

参考文献：

[1] 陈德文.城市轨道交通车辆转向架故障诊断与维修探讨[J].交通世界，2020（12）：140-141.

[2] 李大勇，陈明可，栾林昊，等.转向架在线监测与诊断系统在青岛地铁的应用[J].都市快轨交通，2021，34（3）：34-39.

[3] Zhao C，Feng Z P.Application of multi-domain sparse features for fault identification of planetary gearbox[J].Measurement，2017，104：169-179.

[4] Yan X A，Jia M P.A novel optimized SVM classification algorithm with multi-domain feature and its application to fault diagnosis of rolling bearing[J].Neurocomputing，2018，313：47-64.

[5] Ye Y G，Zhang Y X，Wang Q B，et al.Fault diagnosis of high-speed train suspension systems using multiscale permutation entropy and linear local tangent space alignment[J].Mechanical Systems and Signal Processing，2020，138：106565.

[6] 贺志军，李军霞，刘少伟，等.CEEMD-VMD与参数优化SVM结合的托辊轴承故障诊断[J/OL].机械科学与技术：1-7[2022-11-29].DOI：10.13433/j.cnki.1003-8728.20220290.

[7] 王涛，杨尚骏.基于LMD和SSA-SVM的电机故障诊断[J/OL].重庆工商大学学报（自然科学版）：1-9[2022-11-29].http：//kns.cnki.net/kcms/detail/50.1155.n.20220930.1545.002.html.

[8] 谷湘煜，祝礼佳，柳胡南，等.基于空时域信息融合的水面垃圾显著性检测[J].电子测量技术，2022，45（11）：154-160.

[9] 张延琛.基于时域特征的风机轴承PSO-RBF故障诊断[J].现代制造技术与装备，2022，58（10）：13-16，20.

[10] 储节磊.受限玻尔兹曼机模型优化及其深度表征学习研究[D].成都：西南交通大学，2020.

[11] Hinton G E.Training products of experts by minimizing contrastive divergence[J].Neural Computation，2002，14（8）：1771-1800.

[12] Case Western Reserve University Bearing Data Center. Bearing data center fault test data[EB/OL].[2018-07-15].http： / /www. eecs.case.edu/laboratory/bearing．

【通联编辑：梁书】