单元设计 整体把握

【摘要】实施单元整体教学设计，有助于学生构建知识网络的同时提高思维品质。良好的思维品质一旦形成，就会进入良性循环，处于自主建构的状态，从而成为推动学生个体健康发展的核心驱动力。因此，研究单元整体设计的策略具有重要意义。本研究以“直线与方程”一单元的教学设计为例，从教学目标确定、教学要素分析以及教学流程设计三个层面，讨论了单元整体设计的步骤和流程。

【关键词】高中数学；单元设计；“直线与方程”

【中图分类号】G633.6【文献标志码】A【文章编号】1004—0463（2022）09—0116—04

目前，大部分教师的教学设计拘泥于单课时内容的就课论课，一方面缺少了整体上的把握，另一方面对各个教学要素的选择和应用缺乏回旋余地。而单元教学理念的应用，有效解决了上述问题。它与传统单课时教学相比较，更具有系统性，更有利于学生数学知识网络的构建，更有利于学生数学核心素养的提升[1]。下面，笔者以“直线与方程”一单元的教学设计为例，就如何在分析课标、学情、教材等基础上，设计整单元教学流程，谈谈自己的体会。

一、单元教学目标的确定

教学目标是课堂教学的灵魂，在教学活动中发挥着指向、激励和评价等多方面的作用[2]。在教学设计中科学、合理地确定教学目标，对教学活动的顺利进行具有十分重要的作用。

首先，对教学内容，主要侧重于了解整单元知识在整个高中数学学习中的地位以及本单元的重难点知识，同时包括例题、习题及它们承载的方法、规律和结果的分析。其次，对学生，主要通过观察、提问、测试等方式，分析学生的知识准备情况、能力水平、身心成熟程度和学习动力状态等。最后，在此基础上，确定单元教学目标。

比如，教学“直线与方程”一单元之前，笔者通过课前知识清单填写以及课前小测试，了解了学生的知识储备情况，发现大部分学生存在数形转化能力低下、没有领悟方程思想等问题。同时，考虑到这一单元的知识对学生而言较为抽象。笔者确定本单元的教学目标为：用解析几何的思路和方法研究直线问题，建立平面直角坐标系；通过研究直线方程所具有的性质，从而得出直线的性质；将几何问题代数化，初步给学生渗透用代数方法解决几何问题的方法，体会数形结合的思想。

二、教学要素分析

1.对教学内容的整体分析。不仅要分析教学重难点，还要分析教学内容在整个高中数学中的地位和作用。同时，还要对比新旧教材内容容量、课时等各方面的不同，为教学方案的设计奠定良好的基础。

比如，设计“直线与方程”一单元的教学方案时，笔者主要分析了以下内容：

（1）本单元在高中数学中的地位与作用。本单元的内容是第四章圆与方程以及选修中圆锥曲线的学习基础，同时是用图解法解决线性规划问题的知识铺垫，也是由“等”过渡到“不等”的数学基础，可以说本章是高中数学体系中的“交通枢纽”。

（2）本单元的教学重难点。教学重点：以解析几何为基点，通过直线的倾斜角与斜率得到直线方程；根据斜率判定两条直线平行与垂直、相交以及得出交点坐标。教学难点：一般式下两直线平行或垂直位置关系的判断问题；利用等面积法推导点到直线的距离公式。

（3）本单元新旧教材对比。把新旧教材作比较后发现，就内容而言，旧教材按照学生知识掌握的难易程度依次呈现，而新教材以数形结合思想为贯穿全章节的主线，在平面直角坐标系中，通过直线的具体图象，确定直线的代数性质和几何性质，符合学生的认知规律。这就要求教师在设计教学方案时，要设计具有“坡度”的问题，以问题引导学生的思路，让他们通过探究自己获得知识。

在内容安排上也有微调，与旧教材相比较，两条直线平行与垂直的判定放在了直线方程之前，删了两直线的夹角与曲线和方程的关系等相关内容，开设了“思考”“观察”“探究”等栏目，穿插了“阅读与思考”等内容，增加了教材旁注。说明新教材更注重学生数学核心素养的培养，这就要求教师要转变以前教教材的旧思想，要重视学生各种能力的培养，尤其要重视发挥学生的主体作用。

2.对课程标准的分析。新课程标准是教学的导航，认真研读新课程标准，有助于顺利完成以下教学目标：（1）渗透并引导学生用代数方法研究几何问题。（2）熟悉确定直线的两个条件和两种方法，明确直线方程的系数确定直线的几何特征，斜率和截距决定直线的位置关系。（3）帮助学生领悟数形结合思想和分类讨论思想。

3.对学情的分析。（1）知识储备与能力提升。学生在初中已经学习了一次函数，高中初步学习了立体几何相关知识，既掌握了代数解题方法，又获得了几何感性认识。在此基础上学习直线与方程，可以说是对点、直线的再认识、再深化。通过代数计算结果反馈直线位置关系，让学生体会几何问题代数化的思维方法。（2）突出问题。虽然在立体几何中出现过两个平面所成的二面角α的范围是：0°≤α≤180°，但未曾求过大于90°的角度问题，且教材上从未出现过此类型的例题或习题。初中阶段学习三角函数的定义仅局限于直角三角形，没有涉及过求钝角的正切值和0°角的正切值，而诱导公式等内容未学。

因此，教师在教学时应遵循以下原则：一是由特殊到一般的原则。体现在先学习直线方程的几种特殊形式，再研究具体的几何特征，而后给出直线方程的一般式。二是实践性原则。从本章开始设计的实际问题，到后来在探究发现中的魔术师的地毯问题，都注重学生应用数学知识解决实际问题能力的培养。三是数形结合的原则。本章始终贯穿数形结合思想，教师要引导学生在图形的研究过程中注意代数方法的使用，在代数方法的使用过程中加强与图形的联系，以培养学生数形结合的意识。

三、教学流程设计

根据高中学生易于控制自身注意力、乐于合作探究、勤于思考与发现等特点，本单元采用基于校情的教学方法——“学、问、思、辩、行”五字教学法。教学中，通过尝试解决设置的问题，让学生经历“独立思考——师生交流——归纳提升”的学习过程。教师在学生独立完成的基础上，引导学生对基础知识归纳、总结，并对易错、易混知识通过问题驱动的方式引导学生辨析、梳理。为了突破难点，本单元设计了探究与发现环节，选择了一个几何问题和一个代数问题，设置了“独立思考——小组合作——交流分享”的学习流程。通过该环节，让学生体会代数和几何之间的关系，形成数形结合思想和转化化归思想。

本单元教学应注意以下几点：一是直线方程的表示形式由特殊到一般，教学中特别要注意各种直线方程的使用条件，以及不同形式直线方程的特点，加深对不同形式直线方程的理解。二是直线方程的一般式反映了直线方程在形式上的特点，教学中教师应充分揭示直线方程本质属性，建立二元一次方程与直线的对应关系。在含参数的直线方程的一般式下研究两直线平行与垂直是本章的教学重点和难点。在教学中，教师应注重引导学生分析解题思路，培养学生的数学思维能力和分类讨论的意识，为后续学习“曲线方程”打下基础。三是让学生明白确定一条直线所需的条件，感受直线的方向向量。同时，让学生深刻理解截距的定义。

结合教材知识内容和教学目标，本单元的教学环节设计如下：

探究1：设直线l的斜率k满足∣k∣<1，指出直线l的倾斜角α的取值范围。

师：倾斜角为锐角时，斜率正负如何？倾斜角增大时，斜率如何变化？倾斜角为90°时，斜率如何？

设计意图：通过探究1归纳倾斜角、斜率的概念和它们之间的关系；通过问题驱动学生经历“数”与“形”对应的过程，领悟数形结合思想。

师：两条直线垂直时，它们斜率的乘积都是-1？平行线间的距离公式是如何推导的？你学过哪些距离公式？你认为所学距离公式中最核心的是哪一个？

设计意图：引导学生体会：方程中的代数要素（参数a）如何影响着两条直线的几何要素（它们的位置关系），感悟数形结合思想。

通过探究2研究两条直线之间的位置关系，交点坐标及距离公式；问题一二的设置是为了使学生对所学知识有更深入的认识，这是章节小结的重要目的之一。此时，我们可以借助对探究2中问题的思考，再抛出两个问题：问题1针对直线系方程，问题2针对点到直线的距离公式的几何意义进行深入研究。学生完成这两个问题之后，本节知识将会达到全面的升华。

问题1：求经过两条直线2x-3y+10 = 0和3x+ 4y -2=0的交点，且垂直于直线3x-2y+4= 0的直线方程；求经过两条直线2x+y-8=0和x-2y +2 =0的交点，且平行于直线4x-3y-7=0的直线方程；求经过两条直线2x+y-8 =0和x-2y+2=0的交点，并且经过点P（3，5）的直线方程。

设计意图：逐步渗透“数”与“形”之间的转化意识，为尽早形成数形结合意识打下基础。

探究4：证明三角形两边中点所连线段平行于第三边且等于第三边的一半。

师：在初中我们用平面几何知识能够完成以上证明，那么同学们能否用代数方法完成以上证明呢？

设计意图：引导学生如何使用代数方法刻画距离和两条直线的位置关系，让学生经历把几何问题代数化，用坐标表示点，用方程表示直线；通过直线方程斜率之间的关系，得出直线的位置关系；渗透转化和化归的数学思想方法。

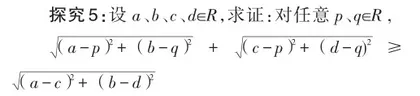
设计意图：引导学生观察代数式的结构，发掘它的几何背景，从而利用几何直观化解该问题。学生经历了将几何问题代数化后，那么自然遇到代数问题，会想到它背后的几何背景，探究发现“数”与“形”之间的密切联系。

总之，“直线与方程”作为高中平面解析几何的第一章，既是对初中所学“一次函数”的延展，又是后续学习“圆与方程”“圆锥曲线与方程”的基石，它起着承上启下的作用。在用有序实数对表示点之后，直线作为平面中最简单的图形，它的坐标化既是自然延续，又是圆与圆锥曲线坐标化的前提。这体现了教材编排的系统性，以及由易到难、由浅入深的编排特点。而坐标法作为连接“形”与“数”的桥梁，集中体现了数形结合的数学思想。因此，本章的学习中，教师既要对本单元主要内容进行梳理，使学生形成系统的知识结构，又要通过重温坐标法研究几何图形的基本思想，为后续数学学习打好基础。

参考文献

[1]许薇嫣.直线与方程单元学习策略探究[J].数理化学习（高一二版），2018（09）：43-44.

[2]雷晓莉，吴鹏，高军，等.单元教学模式的构建与实践——“直线的交点坐标与距离公式”单元教学设计[J].中小学数学（高中版），2013.

（本文系2021年度甘肃省“十四五”教育科学规划课题“核心素养视域下的高中数学概念课教学策略研究”的研究成果，课题立项号：GS[2021]GHB1142）

编辑：谢颖丽