核心素养视阈下小学数学结构化教学的实践探究

结构化教学有利于教师合理把握知识体系的整体框架，用整体和连续的眼光深度理解教材。小学数学教学中，教师要充分研读教材、研究课堂、研究学生，促进知识结构化、认知结构化、思维结构化，让深度学习真正发生。本文以《平行四边形的面积》的教学实践与反思为例，论述核心素养视阈下结构化教学如何提高教学效果。

一、重构知识板块，搭建网络模型

《平行四边形的面积》是建立在平面图形特征以及前期面积意义及长方形、正方形面积计算的基础上学习的。多边形面积的学习，一是通过积累活动经验，运用旧知迁移学习及运用相关的转化数学思想方法；二是学生在利用旧知获得新知的体验上，发展空间观念的同时，积累图形学习方面的活动经验，提升数学核心素养。

对于平行四边形面积计算公式的推导，学生经历了以下三个步骤：①设置实际问题情境：两个花坛哪个大？引起学生前置知识的回忆，实质是理解 “面积比较”的真正含义。②用数方格的方法求面积，启发学生思考：这样 “数”方便吗？从而引出：如果不数，能否求出面积？③探索平行四边形面积计算公式，经历完整的数学建模过程。

学生对于等量代换及转化思想的学习经验，要基于小数乘法转化为整数乘法的计算等，但对图形进行转化，是一种新的学习体验。建构知识板块、搭建网络模型是教师把握教材的核心环节，如何帮助、引导学生发现转化的方向，如何掌握转化的方法，如何引导学生寻找“变化中的等量关系”等是重构知识板块的关键。在重构教学过程和迁移发现学习中，积累的学习经验就体现出学科素养培养的核心所在。

二、精心设计教学，构建数学体系

根据以上的分析，本课设计突显围绕“操作—比较—推理”三大逻辑推理环节展开教学。

环节A：猜想埋伏，激趣探究

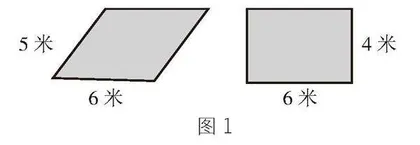
情景：如图1，学校给五（1）班和五（2）班分了两块菜地，一块是长方形的，一块是平行四边形的，哪块的面积大呢？

教师：请同学们先猜想一下，你认为这个平行四边形的面积是多少？（板书：猜想）

预设①：用6×5=30cm2，追问：怎么想到用底×它的邻边？

预设②：用6×4=24 cm2，追问：怎么想到用底×高？联想到什么规律才想到用底×高？

预设③：用数方格的方法。

本环节引导学生大胆猜想平行四边形的面积，并且让学生交流猜想的依据，目的是引导学生有逻辑地思考。

环节B：操作验证，总结公式

活动一：用数方格的方法验证：底×它的邻边。

教师：刚才有的同学认为用底×它的邻边，算出这个平行四边形的面积是30cm2，这样算对不对呢？我们用数方格的方法来验证一下。

通过数方格，我们得出24个1cm2的小方格，而不是30cm2，看来求平行四边形的面积时不能用底×它的邻边（板书：×）。

活动二：用转化的方法验证：底×高。

1.操作。把平行四边形转化成长方形。怎样把这个平行四边形转化成一个长方形？动手操作。预设①：沿着平行四边形其中一个顶点处的高剪下一个直角三角形，拼成长方形。预设②：沿着平行四边形边上一点的高剪下一个梯形，拼成长方形。预设③：其他可能的方法。

2.比较。研究拼成的长方形与原来的平行四边形之间的关系。操作后思考两个核心问题：剪拼后，什么变了？什么没变？

3.推理。反思后总结公式。

本环节以大胆猜想和验证猜想为任务驱动，让学生在自主探究和小组合作中自主构建推理模型：平行四边形的哪些量是不变的？哪些量是变的？在变与不变中如何推理？于变中抓不变量，以等积变形实现联结。

三、自主理解结构，构建思维方式

从结构化教学的实践意义看，全课设计围绕清“面积”之意义、破“底边×邻边”之误判、找“转化”之关键、理“比较”之思路、导“推理”之表述、练“公式”之应用、辩“底高”之对应和拓“等底等高”之认识，让学生经历逻辑推导的严谨过程。

清“面积”之意义。以学生的已有经验为基础，让学生开展方格纸的比对度量活动。引入新课时，引导学生用数学的眼光观察图形，从熟悉的长方形面积入手，回忆长方形面积公式表达形式的实际意义，再通过类比与正向迁移，进一步理解平行四边形的面积内涵。

破“底边×邻边”之误判。长方形面积的计算公式会引发学生产生“负猜想”：平行四边形的面积计算是否也类比于用邻边相乘的方法？学生有此猜想，这是因为受长方形面积公式表达形式负迁移的影响，而忽视了长方形面积公式是一个度量结果的实际意义。本课的设计，就是抓住这样的“误判”为教学切入点，引发学生深思的同时，也为探究求证埋下伏笔。

找“转化”之关键。本课的转化采用剪拼的方法，转化前后图形的形状虽然发生了变化，但面积大小依然不变，属于等量转化，这是本课运用转化思想最关键之处。

理“比较”之思路。纵观整节课的教学，不管是哪一种方法导学，教师都会引导学生经历将平行四边形转化成面积相同的长方形，即等积变形的过程，再通过观察、比较，寻找图形之间的关联。用“比较”理清“变中的不变量”，真正理解转化的实质含义。

导“推理”之表述。此课设计的“三扣环节”，从“操作—比较”再到最后的“推理”，引导学生理解其中的“推理奥妙”和逻辑思维，进而培养学生的高阶思维。

练“公式”之应用。本课还可设计基础、变式、拓展三梯度的练习，旨在让学生在巩固基础知识的同时，深刻理解、灵活变通，真正做到学以致用。

辩“底高”之对应。辩“底高”之对应的练习，既突出了本节课的学习重点，又帮助学生实现了知识的整体建构，彰显了数学的简洁和逻辑。

拓“等底等高”之认识。学生通过对比、反思，深切地感悟到平行四边形面积计算公式中于“等底等高”在面积计算中的特殊意义，从而帮助他们打破面积计算时建立起来的，根据图形的边线长度计算面积的思维定式。

综上所述，教师善于重构数学知识体系、知识网络与思维方式，学生就能够在感知知识的整体性和结构化的同时，经历“数学抽象、逻辑推理、数学建模”等思想方法，提高自主探究学习能力。

注：本文系广东省教育研究院2022年度中小学数学教学研究专项课题“基于核心素养导向下小学数学教师专业素养发展研究”（课题立项号：GDJY-2022-M-b28）的研究成果。

责任编辑 罗 峰