博士学位授予单位立项建设对高校内涵建设的推动作用及成效
作者: 唐多毅 张雪松
[摘 要]博士学位授予单位立项建设是高校获得博士学位授予权的必由之路。文章通过对高校发展内在驱动力与外部驱动力的分析,论述了博士学位授予权对高校发展的重要意义;在明确博士学位授予单位立项建设是高校内涵建设主要任务的基础上,分析了立项建设对研究生培养、学位点建设、人才队伍建设、学科建设、服务创新、资源及质量保障体系完善等的推动作用;并以中原工学院为例,采用基于群决策的AHP-Fuzzy评价方法对博士学位授予单位立项建设的成效进行了综合评价与对比分析,结果发现经过博士学位授予单位立项建设,学校的内涵建设水平有了显著提升,特别是对学科建设的带动作用十分明显,同时也明确了需要进一步加强建设的工作。
[关键词]博士学位授予单位立项建设;学科建设;研究生培养;学位点建设
[中图分类号] G643.7 [文献标识码] A [文章编号] 2095-3437(2023)15-0001-05
博士学位授予单位立项建设是一项具有中国特色的学位管理制度,是立项建设高校以获得博士学位授予权为目标而开展的建设工作。博士学位授予单位立项建设工作最早源于1998年湖北省学位办向教育部提出的开展学位点立项建设的建议,经过试点,教育部于2008年正式开始全面推广这项工作,首批确定了50个博士学位授予权立项建设单位,此后,各省也逐步建立了博士学位授予单位立项建设制度,并将此作为向教育部推荐新增博士学位授予单位的先决条件。至此,博士学位授予权审核已经从单纯的条件审核转变为以建设为重点、以高质量发展为本的新模式[1-2]。
博士学位授予单位立项建设制度的核心在于建设,强化过程管理,强调高质量推进学校的均衡发展,促使高校在立项建设过程中厚植学术根基,蓄积发展动力,最终达到获得博士学位授予权的条件。本文拟对博士学位授予单位立项建设在高校内涵建设中的推动作用进行分析,并以中原工学院的博士学位授予单位立项建设为例对其成效进行分析[3]。
一、高校获取博士学位授予权的内在驱动力与外部驱动力
(一)获取博士学位授予权是高校增强发展内在驱动力的必然要求
高校获得硕士学位授予权后,办学层次从原先单一的本科教育逐渐向本科教育与研究生教育并重转变,建设高水平研究型大学成了大多数拥有硕士学位授予权高校的强烈愿望。争取博士学位授予权,是高校提升办学层次的迫切需要,也是高校学科建设和硕士研究生教育发展到一定阶段的必然要求,是高校实现自我突破、争取更大发展空间的必然选择[4]。
(二)高校之间竞争激烈是高校争取博士学位授予权的外部驱动力
拥有研究生招生、培养资格体现了高校人才培养的层次,也显示了高校办学的整体实力与水平。博士研究生教育是高校人才培养工作的高峰,是夯筑学科基石的重要途径。高校在“双一流”建设目标的驱动下,取得博士学位授予权是高校学科建设发展的必争高地,也是高校实力竞争的重要依托[5]。
二、博士学位授予单位立项建设对高校内涵建设的推动作用
博士学位授予单位立项建设制度的建立,意味着学位授予权审核制度由过去的以行政审核为主改为以经济社会发展需求为导向,以学术审核为主、行政审批为辅,以学校的办学质量和办学水平为先,兼顾学位授予权的学科、区域和类型分布等情况。
(一)助力推动学科建设上层次上水平
博士学位授予权是国家在高校学科建设水平达到一定高度后给予的一项人才培养授权。搞好学科建设是争取博士学位授予权的基础,是一项根本性、基础性和战略性的任务。在开展博士学位授予单位立项建设时,首先要根据社会经济的发展需求优化学科布局;其次要完善学科组织,提升学科的学术生产能力与产出效率;此外,还要加强学科队伍和学科载体的建设,凝练学科方向,形成发展合力。从某种意义上说,博士学位授予单位立项建设就是学科建设[6]。
(二)助力高标准高质量建设硕士学位授权点
博士学位授权点是比硕士学位授权点层次更高的人才培养平台。博士学位授予权审核对人才培养方向、教师队伍建设、科学技术研究、教学科研支撑等方面都提出了更高的标准,对招生选拔、思政教育、课程教学、导师指导、学术训练、学术交流、论文水平、质量保证、学风建设、管理服务、就业发展等都有明确的要求。开展博士学位授予单位立项建设,有助于全面提升现有硕士学位授权点建设的水平和质量。
(三)助力优化人才队伍结构
博士学位授予单位立项建设过程中,通过开展人才队伍建设,引进战略性高端拔尖人才、创新人才等,有助于增强重点学科、特色学科学术队伍的能力,优化人才梯队,促进学科发展和高层次人才培养。在加强人才队伍建设的同时,还可有效推进学校的人事制度改革,优化人才发展软环境,建立起一套适应学校发展要求的激励保障机制,激发人才活力。
(四)助力优化研究生教育保障体系
加强保障体系建设是促进研究生教育水平提升的重要举措。在推动博士学位授予单位立项建设过程中不能离开保障谈建设,建立完善的保障体系是有效开展学科建设、人才培养、条件建设的根本保证[7]。
三、博士学位授予单位立项建设对高校内涵建设推动作用的评价与分析
我国开展博士学位授予单位立项建设工作的时间不是很长,部分高校对其建设规律的认识还不够深入,很多情况下大家对建设工作的关注点主要集中在各项指标的达成情况,而没有去综合评估其对学校内涵建设的推动作用与成效。建立一套科学合理的评价体系有助于充分认识这项工作的重要性和必要性。
(一)评价指标体系
根据高等教育评估的一般要求,结合博士学位授予权审核条件,采取定量与定性相结合、客观与主观相结合的办法科学合理地构建评价指标体系。在广泛调研、充分论证的基础上,选取以科学研究、师资队伍建设、支撑平台及条件建设、人才培养、博士学位授予权支撑学科建设等5个方面为目标层指标即一级指标,选取13个指标为准则层指标即二级指标,选取46个评价层指标即三级指标,共同构建起博士学位授予单位立项建设成效评价指标体系[8-9]。
(二)评价方法及步骤
1.基于群决策的AHP-Fuzzy评价方法
博士学位授予单位立项建设成效的评价指标涉及的内容广泛,其中有很多指标难以用精确的数学表达式进行量化,这就造成评价困难。因此,有必要采用层次分析法(AHP)和多层次模糊综合评价法(Fuzzy)相结合的方式进行评价[10]。
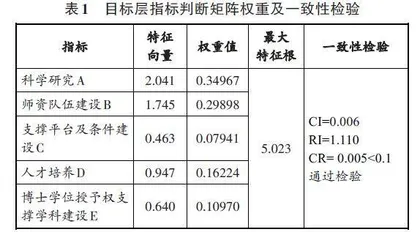
2.建立判断矩阵及一致性检验
采用层次分析法进行评价时,首先要建立判断矩阵。比如中原工学院为了使判断矩阵各要素的权重值更科学、合理,特邀请了7位来自不同高校具有教授职称的专家,包括长期从事学科建设和研究生教育管理的部门负责人、学科带头人等,对各项指标进行综合等级评定。7位专家根据各自的判断,给每组要素建立相应的判断矩阵,然后采用加权几何平均法对群决策进行综合计算并得出最终权重结果。
设有 [s] 位专家参与某组要素判断,分别建立判断矩阵 [A1, A2, …, As],其中
[Ak=aij, k k=1, 2,…, s] [ (1)]
对 [A1, A2,…, As]矩阵采用加权几何平均法可得到一个综合判断矩阵 [A=aij], 其中
[aij=aij, 1λ1∙aij, 2λ2∙…∙aij, sλs i, j=1, 2 ,…, nk=1s λk=1 (2)] 式中, [λ1, λ2,… ,λs]为专家权重系数,当权重系数取相同值时,[λi=1s, i=1, 2 ,… , s] , 此时
[aij=ai j,1⋅aij, 2∙…∙aij, s1/s i, j=1, 2 ,… , n (3)]
该方法可保持判断矩阵A的互反性, 如Ak (k=1,2,…,s)均满足一致性条件时则合成后的综合判断矩阵 A也满足一致性, 当 Ak中有不满足一致性的矩阵时则A不一定满足一致性。
对于一组群决策,其总体标准差
[σij=1s-1k=1s aij, k-aij2 i, j=1, 2,…,n (4)] 当 [σij<ε] 时, 这组判断认为是可接受的,否则应将信息反馈给各位专家, 让他们考虑作适当修改后再进行计算。这里[ε] 是一个给定的值,一般可在[0.5,1]之间取值。
先是构建一级指标判断矩阵。7位专家根据各自的判断,按照1-9标度法对指标评价中的两两重要性进行赋值,分别建立判断矩阵[A1, A2, …, A7]。
[A1=113 2 3113 2 31/31/311/211/21/22 1 21/31/311/21],
[A2= 1 14 24 1 14 241/41/411/211/21/22 121/41/411/21],
[A3= 1 25 3 41/2 14 2 31/51/411/21/21/31/22 1 21/41/321/2 1],
[A4= 1 24 331/2 12 221/41/211/211/31/22 111/31/21 11],
[A5= 1 13 2 2 1 13 2 21/31/311/21/21/21/22 1 11/21/22 1 1],
[A6= 1 14 2 3 1 14 2 31/41/411/31/21/21/23 1 21/31/321/2 1],
[A7= 1 14 3 4 1 14 3 31/41/411/41/31/31/34 1 21/41/331/2 1]
上面7个判断矩阵的CR值分别为:CR1=0.003,CR2=0,CR3=0.015,CR4=0.012,CR5=0.003,CR6=0.008,CR7=0.056,CR值均小于0.1,满足一致性要求。
由几何平均法求得综合判断矩阵A=