九年级数学第一轮复习有效作业设计探究

摘 要：随着新课程改革的不断深入，数学作业的设计也要不断创新，教师需要继承和发扬传统数学作业的优点，舍弃其弊端，以学生的终身发展为目标，设计形式多样、接近生活、且学生乐于接受的有效作业。本文根据九年级第一轮复习的特点，就作业设计的原则、操作形式与方法等方面作了探究。

关键词：第一轮复习； 作业设计； 原则； 方法

中图分类号：G633.6 文献标识码：A 文章编号：1006-3315（2016）02-029-003

一、问题的提出

第一轮复习非常重要，它是整个九年级复习的基础和关键，起着承上启下的作用。在这一阶段主要抓好对基本概念准确记忆和实质性的理解，抓基本方法、基本技能的熟练应用，抓公式和定理的正用、逆用、变用、巧用，抓基本题型的训练。教师会根据作业情况对自己的教学方式和教学内容作及时的调整和反思，归纳和总结典型错误，并在以后的教学中加以改进，所以我们必须精心设计有效的作业，提高效率。通过问卷调查和目前教学现状表明，由于数学作业设计质量不佳的原因会普遍引起以下几个问题：

（一）课堂教学中习题质量不高，导致学生基础知识掌握不扎实

在第一轮复习过程中，教师没有很好选取课堂习题，片面的追求复习进度来完成了对知识内容的复习。这样似乎节省了很多时间，但实际上学生在复习过程中，对于很多知识尤其是七年级和八年级的知识已经不熟悉甚至遗忘，这样的复习会导致学生第一轮复习过后对基础知识的掌握仍然不扎实，从而影响第二轮的复习。

（二）教师布置作业比较随意，导致学生降低对学习数学的兴趣

新课改实施以来，大部分教师以新课改理念为指导，不断地优化自己的教学行为，学生的学习逐渐成为一个快乐的过程。但有不少教师在设计和布置作业时没有明确的目标和清晰的意图，缺乏必要的思考，如教师通过各种方式让学生购买教辅资料，如当堂检测，孟建平数学，优化与提高，中考模拟等等，利用这些资料让学生强化性做题，不仅浪费学生的时间，不能很好的促进学生的发展，还会降低甚至失去对数学学习的兴趣。

（三）作业的设计缺乏实践性和创造性，导致学生缺少解决实际问题的方法

数学源于生活，也应用于生活。教师要善于联系生活实际进行作业设计，充分展现数学的应用价值，让学生在生活中体会“处处有数学”。应考虑让学生用所学的数学知识解决实际生活中的问题，锻炼学生的创新思维。在实际复习过程中教师由于多方面的原因，作业中很多掺杂了些繁、难、偏、旧、机械的、滞后的题目，缺乏联系生活实际，教师和学生可能很辛苦，但是复习效果较差。

二、数学复习课作业设计的原则

（一）作业设计要体现基础性

每年的中考题安排了较大比例的试题来考查“双基”，所以复习中要紧扣教材，夯实基础。要在这部分试题上保证得分，就必须结合教材，对整个初中阶段需要掌握的内容心中要有清晰的脉络；其次，复习应配备适量的练习，习题的难度要加以控制，以中等题和简单题为主。

案例一：在复习到平方根和算术平方根概念之后，设计了这样一组题：

1. 2的平方根是（ ）

A.4 B.C. D.±（12年江苏）

2. 4的算术平方根是

A.±2 B. 2 C.-2 D.（15年浙江湖州）

3. 化简：=（ ）

A.2 B.-2 C.4 D.-4（12年甘肃）

4. 化简=_________。（13年安徽）

通过精选近几年中考题中涉及相关章节知识点的中等题和简单题，让学生有针对性地进行适量训练，既巩固了当天复习的内容，也能使学生进一步了解中考命题特点，激发兴趣，增强数学学习的信心。

（二）作业设计要体现趣味性、实践性

教育和发展心理学巨匠皮亚杰说：“所有智力方面的工作都要依赖于兴趣。”兴趣是最好的老师。但长期以来，由于教学任务比较重或受习惯性思维影响，教师在设计作业时没有多加思考，缺乏明确的目标和清晰的意图，使很多的学生降低了学习的兴趣，同时也失去了学习数学的灵气和创造的激情。要想改变这种状况，在作业设计中，必须要适当增强作业的趣味性、实践性。这样才能让学生在作业中集中注意力，并保持饱满的热情，从而提高作业的质量，使其形成良好的兴趣和爱好。

案例二：当学生复习有理数的加、减、乘、除混合运算后，设计了如下题目：有一种“二十四点”的游戏，其规则是这样的：任意四个1～13间的自然数，将这四个数（每个数用且只能用1次）进行加、减、乘、除运算，使其结果等于24。如对1、2、3、4所作运算：（1+2+3）×4=24。

（1）现有四个有理数3、4、-6、10运用上述规则写出三种不同方法的运算，使其结果等于24。

（2）现有四个数3、-5、7、-13仍运用上述规则，写出一种运算式，使其结果等于24。

算24，这是生活中的扑克游戏，学生在这类似游戏的快乐作业中，加强了“双基”，增强了阅读能力和按规律研究的意识，也提高了对数学学习的兴趣。

（三）作业设计要体现层次性

对于第一轮复习必须坚持作业设计体现基础性，但不同的学生肯定是有差异的，那么在关注中等及以下同学发展的同时，我们还应该重点关注那些数学尖子生，让尖子生仍能积极思考，激发其兴趣，所以笔者认为在作业布置时必须有层次性。

案例三：笔者把作业分为三个层次。A组——基本题。重在“双基”训练，适合“学困生”；B组——变式题。培养学生的迁移能力，适合“中等生”；C组——创新题。培养学生创造性解决问题的能力，适合少数“尖子生”。下面举例说明：

第一层： A组 基础性题目

1.已知：在Rt△ABC中，∠C=90°， AC=4 AB=5，求cosA的值。

2.已知：在△ABC中，∠C=90° E是AC边任一点，且ED⊥AB，垂足为D，交AB于D。求证：△ADE∽△ACB。

第二层：B组 提高题

1. 已知：在Rt△ABC中，∠C=90°，如果sinA是方程2x2+3x-2=0的根，求cosB的值。

2.已知：在△ABC中，∠C=90° AC=8 BC=6，点D、E分别在AB、AC边上，且DE垂直平分AB，求DE的长。

第三层：C组 开放性或探究性题

1.在某海域中有一海岛A，它的四周20海里范围内为暗礁区。一艘轮船由东向西航行，在B处见岛A在北偏西60°，航行24海里到C处见岛A在北偏西30°，货轮继续向西航行，有无触礁危险？

这样，不同层次的学生能比较轻松地完成他们的相应作业，使他们的数学基础都能在原有的基础上得到较大的提高。同时，我还适时鼓励大家向更高层次的作业挑战，培养他们战胜困难的勇气。教师要树立“只有差异，没有差生”的观念，让不同水平、不同层次的学生能体验到成功，尤其是创新成功。

三、数学复习课作业设计的形式与方法

（一）知识性作业的设计

1.按知识结构设计作业层次。一般可以有三类，A级为基本练习：重在基础知识和基本技能的操练，浅显易懂，紧扣当天所学的内容；B级为提高练习：重在对知识的理解和运用，难易尺度是学生“跳一跳，够得着”；C级即创新练习：重在对概念的深刻理解和灵活运用，这种题目有一定的难度。

案例四：如在复习一次函数的概念后，可以设计这样一份作业：

一、填空题

（A）（1）已知函数y=（m+1）x+2m-4当m_______时，它是一次函数；当m______时，它是正比例函数。

（B）（2）若一次函数y=2m（x+1）-4表示正比例函数，则m=_____。

（B）（3）已知函数y=（m-3）x +m+1是关于x的一次函数，则

m=___。

二、解答题

（B）（4）已知函数y=（k2-4）x-k

①当k为何值时，这个函数为正比例函数？并求解析式；

②当k在什么范围内取值时，这个函数是一次函数？

三、探究题

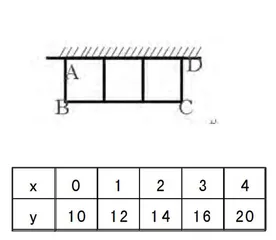
（C）（5）观察表中，y与x是否成一次函数关系？如果是，求该一次函数的解析式，如果不是，改动尽量少的数字，使其成为一次函数，并写出解析式。

（C）（6）已知2y-2m与3x+4n成正比例，证明：y是x的一次函数。

这样，通过基本的、提高的、创新的不同层级的题组作业，不同程度的学生能够对一次函数以及正比例函数的概念得到最大程度的理解和掌握，并在实际问题中灵活运用。

2.同一类问题设计有梯度

对有一些题由易到难的设置问题，使学生踏着阶梯一步一步探索，让每一位学生都能获得不同程度的成功尝试，激发学生的潜能。从教学效果的角度看，设问的多梯度性可以帮助学生发掘问题的各个方面，达到深层次认识问题的本质，有利于培养学生的纵向思维。

案例五：在复习等腰三角形时，设计如下作业：

（1）如果等腰三角形的一个底角为70度，那么它的顶角是多少度？

（2）如果等腰三角形的一个为顶角70度，那么它的底角各是多少度？

（3）如果等腰三角形的一个内角为70度，那么它的其余的角各是多少度？

（4）如果等腰三角形的一个内角为100度，那么它的其余的角各是多少度？

（5）如果等腰三角形的一个内角为n度，那么它的其余的角各是多少度？

这样，通过以上由易到难的题组作业，学生按照有顺序的、可预测的方向进行纵向思考，在逐步体验数学成功的喜悦的同时，加深了对问题的本质理解。

3.根据易错题设计矫正型作业

通过精心设计典型的作业易错题，及时渗透所学的数学思想方法，能使学生掌握知识的学习任务所需的时间大为减少，学习的达成度就越高。笔者曾经在2010年编写了校本课程二次函数矫正型作业设计，以下是部分内容：

案例六：基于性质的《二次函数》矫正型作业

例1：已知函数y=3x2-4x+1，当0≤x≤4时，求y的变化范围。

【错解】当x=0时，y=1；当x=4时y=33

∴当0≤x≤4时，y的变化范围是1≤y≤33

【剖析】错解是由于对求二次函数值的范围缺乏实质性的认识而造成的，事实上，抛物线在对称轴的左侧时，y随x的增大而减小，抛物线在对称轴的右侧，y随x的增大而增大，于是x=-=时，函数取到最小值-。

【正解】当x=-=时，函数最小值-，所以y的取值范围是-≤y≤33

【矫正练习】

1.若A（-，y1），B（-，y2），C（，y3）为二次函数y=x2+4x-m的图像上的三点，则y1，y2，y3的大小关系是_____。

2.心理学家发现，在一定的时间范围内，学生对概念的接受能力y与提出概念所用的时间x（分钟）之间满足函数关系式y=-0.1x2+2.6x+43（0≤x≤30），y越大，表示接受能力越强。那么，学生在0≤x≤30这段时间内，接受能力y的取值范围是_____。

3.y=-x2+8x-12，在当x≤4时，y有最大值_____。

4.如图，在一面靠墙用长为8米的铝合金制成如图窗框，问窗框的宽和高各为多少米时，窗户的透光面积最大？最大面积是多少？若墙的最大可用长度为3米，则求窗户的透光面积最大？最大面积是多少？

通过易错题的练习，可以提高学生的审题、解题能力和题后反思能力，以起到事半功倍的效果，从而进一步提高数学学习效率。