浅谈几何复习课的教学

摘要：章节复习课难上，几何章节复习课更难上，本文举例分析一堂几何复习课，提出一种复习课模式，并加以诠释。旨在抛砖引玉。

关键词：几何；复习课；模式

中图分类号：G633.6 文献标识码：A 文章编号：1006-3315（2015）06-028-001

笔者有幸参加了一次教研活动，听了两节《勾股定理》复习课后，有意犹未尽的感觉，听课后，自我备了一节复习课，借此谈谈几何复习课的模式和感悟。

一、教学设计

1.情景引入

（1）已知等边△ABC的边长为10，求△ABC的面积。

（2）已知等腰△ABC，AB=AC=5，BC=6，求△ABC的面积。

（3）已知Rt△ABC，∠A=90°，AB=5，AC=12，求△ABC的面积。

（4）已知Rt△ABC，∠A=90°，AB=5，BC=13，求△ABC的面积。

[设计意图]在前面教学时学生对如何计算三角形的面积的条件认识不够，解决此类问题为了进一步解决一般三角形的面积的条件做铺垫。同时在这组问题中包含了勾股定理的一般计算。

2.新课教学

问题1：确定一个三角形需要几条边呢？

问题2：刚才我们解决的是特殊的三角形的面积的问题，那么一般性的三角形需要已知几条边的长度才可以求三角形的面积呢？

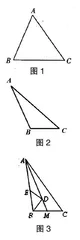
例题1：如图1，在△ABC中，AB=13，BC=14，AC=15，求△ABC的面积。

变式：如图2，在△ABC中，AB=13，BC=4，AC=15，求△ABC的面积。

例题2：在△ABC中，AB=10，AC=17，BC边上的高AD=8，求BC长。

[设计意图]已知三角形的三边可以求出三角形的面积。培养学生的数学思想：分类讨论、从特殊到一般的归纳、方程、数学结合等思想方法。运用“情景导入-探索-建模-应用拓展”的教学模式进行几何复习课的教学。

3.归纳小结

（1）通过例题讲解，可以得出怎样的三角形可以求出三角形的面积

（2）如何求出三角形的面积。

4.应用拓展

如图3，△ABC中，AB=17，BC=10，CA=21，AM平分∠BAC，点D、E分别为AM、AB上的动点，则BD+DE的最小值是。

[设计意图]通过建模，利用模型解决问题。培养学生透过现象看出此题的本质的能力。

二、教学设计中几何复习课的模式

几何复习课一章的复习，一般都是安排两节复习课，第一节课是基本知识，基本图形，基本方法的复习。第二课则是能力的提升和知识技能的升华。本节课就是基于这样的想法而备的一堂课，笔者把它分为四个模块。

1.问题情境创设

情境创设对一堂课的影响是非常大，本节课中从同学们平时常碰到的问题入手，选取在学生的“最近发展区”内。教案中情境引入部分的4个问题是在学习中常遇到的特殊图形的面积问题。其中每一道题均要用到勾股定理来解决。同时给学生留下一个问题，这些特殊三角形面积如何求得，总有意犹未尽的感觉。一个问题就自然生成：一般的三角形的面积如何求呢？它需要哪些条件呢？激发学生的求知欲。

2.建立几何模型

模型教育是几何教学的重要环节，指导学生学会提取不同题目的模型，准确洞察各类问题的本质，在理解的基础上进行变化。本节课中新课教学环节就是提炼模型的环节。让学生体会到三边已知，通过作一边上的高，构造直角三角形求出该边上的高，从而求出三角形面积。通过对一类模型的分析、理解、变通，能让学生理清解题思路，由“做一题”到“会一类”，最终“通一片”，也就是获得解题的通性、通法。这是几何教学的目标。

3.应用拓展模型

应用拓展，就是让学生能拨云见日，培养学生举一反三，触类旁通的能力。本节课中的应用拓展环节就是这样设计的。首先利用“饮马”问题解决最小值的问题逐步将问题转化为已知三边求三角形中的高的问题。

三、教学设计中体现三个“WU”

学生是课堂的主体，本节课教学设计时体现到这一点，给学生留足思考空间，让学生有所思，有所悟，有所得。

1.捂——捂着新知，让学生自行发现探索

在复习课经常被上成“满堂练”的今天，笔者想尝试如何上好一堂几何复习课。本节课通过设计创设情境，让学生在解决特殊三角形的面积的同时，熟悉求出面积所需要的元素，还让学生产生了一些疑问和猜想。进而发问，回答一般的三角形如何解决，需要哪些已知量，最终解决已知三边如何求三角形面积问题。开始捂住我们要解决的问题，让学生带着自己的疑惑解决本节课的问题。把思考权交给学生，不是一味的听老师讲解。

2.焐——让知识发酵，内化，熟练掌握

老师经常想把学生培养成“熟练工”，题海战不可避免。那么学生一定得花大量的精力来解决老师的作业，那么他思考的空间在哪里？笔者在备课时通过一个问题，甚至一个图形，将问题进行变式，让学生在熟悉的问题环境中理清思路，把问题拆解重组。留给学生思考的空间，让学生的知识在这里发酵，内化成自己的，发现解决此类问题的钥匙。

3.悟——让学生理解、灵活运用知识的本质

举一反三，触类旁通是学生学习能力的体现，要给他们充分的创造机会，让他们有机会去理解、应用、发现知识的本质的东西。笔者在备课时充分考虑了这点，在知识拓展环节，让学生能有机会去悟出知识的本质，应用它解决眼前的问题，达到学一知多的目的。

总而言之，数学的课堂要把“学”的权力交给学生，应注重知识发生过程的教育，经历丰富而生动的思维活动过程，经历实践到理论再实践的过程。几何教学中章节复习课也可以做到如新课般生动形象。不只是知识的再现和重复的训练，也可以将一个主题穿插在复习之中。本节备课是勾股定理的应用的复习，通过构建直角三角形来解决线段长的问题，但又有别于简单的习题训练。这样就可以得到知识与能力的齐头并进。