三维进阶：小学数学结构化教学设计策略

美国教育家布鲁纳认为：“学习一门学科，就是掌握这门学科的基本结构。”数学学科结构性强，具备逻辑清晰的知识结构和科学系统的方法结构。但是，在日常教学中，时常出现“碎片”式的教学设计，使学生的学习只见树木不见森林。为此，我们要具备结构化的设计思维，从整体的视角把握教材，分析学情，设计结构合理的教学活动，把零碎的知识串成线、连成片、卷成体，使学生所学的知识具有关联性、结构性、迁移性。基于以上思考，笔者以人教版小学数学“图形的认识与测量”主题为例，谈谈如何通过结构化设计促进学生的深度学习。

一、设计结构化活动，让操作的展开更有层次

数学活动，是指个体通过指令去变换一个客观的数学对象，包括如操作、实验、演算、回忆、猜想、判断等，是组成课堂学习活动的基本元素。在“图形的认识与测量”主题中，画、摆、搭等数学活动是学生体验数学对象的直观背景和结构关联、建立基本活动经验、培养核心素养的重要举措。教师在设计数学活动时应该关注活动的层次性与关联性，以结构化的活动促进概念的有效建构和素养的提升。

1.有结构地“搭”，指向要素的全面理解

立体图形是抽象而复杂的。搭建立体模型的活动，可以化抽象为直观体验，有效帮助学生对立体图形进行分解，深入了解立体图形的特点及各部分之间的关联。教师要遵循从特殊到一般的认知规律，除了让学生对于单个素材进行深入体验，还要对比不同素材之间的异同，让学生全面理解图形要素。

例如，教学人教版小学数学教材五年级上册“长方体的认识”时，为了深入理解长方体顶点和棱长的特征，教师可以设计如下活动。（1）提供三种长度、颜色不同的小棒，小组合作搭一个长方体的框架并回答问题：长方体有几条棱？哪些棱的长度相等？长方体有几个顶点？（2）组间合作，在黑板上完成表格，并展示小组的作品。活动（1）是从单个的、特殊的长方体入手，让学生在搭的过程中初步探索长方体的特征。活动（2）是探究一般的长方体，借助统计、归纳将个体的“搭”汇聚成集体的“搭”。此时，学生会发现一共只有两类长方体，且棱数都是4的倍数。学生在这样从“个例”到“普遍”的探究过程中，全面理解长方体的棱长特点。

2.有层次地“画”，体现概念的层层建构

在图形教学中，“画图”扮演着非常重要的角色，它不仅能让学生的思维显性表达，还能使抽象的概念变得直观形象，使学生更容易理解和记忆。有层次地设计画图活动，有助于学生在学习过程中逐步深化和扩展对概念的理解和应用，由易到难，层层深入。

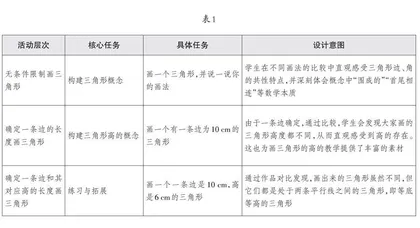
例如，教学人教版小学数学教材四年级下册“三角形的认识”时，教师可以通过“三画”三角形，帮助学生构建起三角形的概念（如表1）。三次画三角形，条件层层收紧，逐步增加三角形的边、高等要素的限制，虽然大家每次画出来的都不一样，但是每次都会有新的认识和体会。最终学生会思考：究竟怎样的规定才能让大家画出一样的三角形。从而深度理解三角形概念。

3.有阶段地“摆”，关注素养的有效提升

小学阶段“图形的认识与测量”主题涉及的核心素养表现主要有：量感、几何直观、空间观念、推理意识。其中，量感主要指对事物的可测量属性及大小关系的直观感知。长度、面积、体积大小的感知及其单位之间的进率实际上就是量感的体现，这也是学习难点。通过阶段性体验“摆一摆”的过程，学生可以逐渐形成对常用单位量级的直观认知，加深学生对单位进率的理解，培养量感。

例如，教学人教版教材小学数学三年级下册“面积单位之间的进率”时，在学习本课之前，受长度单位十进制的负迁移，许多学生误认为1 dm2=10 cm2。而量感的培养要建立在深度体验的基础上。为此，教师可分两个阶段设计“摆一摆”的活动：第一阶段，让学生自由地用1 cm2的正方形纸片摆出1 dm2的正方形，充分展示学生的多样表征，体现思维的梯度。第二阶段，以培养量感为目的，带领学生从1 cm2开始一直摆到100 cm2。此处的重点是体验“10×10”的过程，可以在10 cm2以后直接让学生用10个为一组的小方块接着摆，体会10个10动态生成的全过程。在这期间，教师还可以将10个小纸片集中地摆在一起，带领学生寻找身边类似大小的物品进行对比记忆，然后再和1 dm2做比较，从而消除十进制的负迁移，加深对百进制的理解。

二、构建结构化“学程”，让学习的推进更加有序

学程即学习的进程。在做学程设计时，我们不但要考虑知识的展开序列，还要考虑学生学习的发生序列。也就是说，教师应充分了解教材，将知识内容进行结构化串联，形成系统的教学序列，符合知识发展的逻辑。同时还要根据学生的认知水平和发展规律，调整教学策略和方法，将“有结构地教”转变成“有结构地学”。

1.在认知的重构中构建学程

美国教育心理学家奥苏泊尔指出：“影响学习唯一最重要的因素，就是学习者已经知道了什么。要探明这一点，并应据此进行教学。”在进行图形概念课的教学时，学生往往已经具备了一定的生活经验，对图形有了基本的认识。为此，教学该部分内容的过程其实是对学生认知重构的一种引导。引导过程要符合学生的认知规律，使他们在掌握新知识的同时，不断丰富和优化原有的认知结构。

例如，教学人教版小学数学教材四年级上册“梯形的认识”时，本课的重点是在学生已经认识一般梯形的基础上提炼梯形的基本特征，构建梯形的概念。为此，教师可以设计如下学程：（1）在点子图上画梯形；（2）比较作品，提炼梯形的共性特征；（3）在辨析中概括梯形概念；（4）画特殊的梯形，再次辨析强化概念；（5）认识梯形的组成部分完善概念；（6）巩固练习强化概念。以上设计遵循认知发展规律，从学生已有的经验出发，先将公认是梯形的选出来，提炼共性特征；再利用该特征去判断有争议的作品，在辨析中逐步构建梯形的概念；最后，让学生利用概念创造特殊的梯形，再进行二次辨析，完善概念。整个过程，梯形的概念在反复的辨析强化中螺旋上升（如图1）。

2.在本质的探索中构建学程

在图形领域的学习中，经常会遇到学生已经“知道”公式和结果的情况。此时如果我们还是当作学生“未知”去设计学程，就会导致学生在整个学习过程中失去兴趣，丧失学习的动力与热情，影响学习效果。此时，只要我们转变教学的结构，变“正叙”为“倒叙”，从已知出发，带领学生探寻知识背后的内在本质，就能激发学生学习的内驱力，实现对知识的深度理解与应用。

例如，教学人教版小学数学教材三年级下册“长方形和正方形的面积”时，许多学生已经提前知晓长方形和正方形的面积计算公式。对此，教师可以做如下设计：（1）会计算长方形和正方形的面积吗？计算公式是什么？（2）出示题组，全班学生练习。（3）还有什么问题没解决？引出问题：为什么长方形的面积=长×宽？这样的设计（如图2），就是在正视学生起点的基础上，通过生生互学的方式，直接揭示面积公式，将所有的学生拉至同一起跑线。将公式的习得从课的终点变为起点。将“为什么这么算？”作为本节课探究的核心问题，从而激发学生的学习动机，引导学生深入挖掘长方形和正方形面积计算的本质（如图2）。

3.在思维冲突中构建学程

学习过程实际上就是认知冲突不断被激活再化解的过程。而这些激烈的冲突点往往是最佳的学材，可以转化为一节课的核心问题，从而引发学生的深度思考。因此，教师可以基于学生思维的冲突点，构建结构化的学程。

例如，教学人教版小学数学教材五年级上册“平行四边形的面积”时，由于受到长方形和正方形面积公式的负迁移影响，许多学生想当然地认为平行四边形的面积就是相邻的两条边相乘。由此，教师可以利用这一思维上的冲突点，设计如下学程：（1）出示一个平行四边形，请学生量一量、算一算它的面积；（2）辨析结果，引发冲突：邻边相乘和底乘高，哪种算法正确？（3）验证说理。这样的设计（如图3），就是通过求一个平行四边形的面积引发学生的思维冲突，让学生在主动论证观点的驱动下深入探索，最终在解决问题的过程中实现知识的结构化构建。

三、关联结构化“体系”，让知识的构建更加立体

结构的关联能使认知结成清晰的脉络，形成多维、立体、交叉的体系，这样的认知体系超越课时、超越单元，甚至跨越学段。奥苏伯尔认为，学习的实质就是学生认知的组织和重新组织，组织和重新组织的过程就是新旧知识相互联系、相互作用的过程。为此，教师要站在高位研读教材，考虑教材的“前后左右”，挖掘各文本背后所隐含的内在联系，构建更加立体、多维的知识体系。

1.横向迁移，突破认知拐点

迁移的思维方法是将一种情境中得到的方法、结论应用在另一种情境中的认知活动过程。在图形领域的学习中，有些内容看似是两个完全不同的维度，关联并不明显，但是如果进行深入分析、比较，就会发现隐藏在它们背后的共性。横向迁移这些共性的思想或方法能帮助学生突破认知拐点，形成并行的知识结构。

例如，教学人教版小学数学教材三年级下册“面积的认识”时，其中一项重要任务就是帮助学生将度量的认知从一维跨向二维。这就需要对度量方法进行横向迁移。教师可以在布置度量图形大小的任务之前，带领学生回顾长度的度量方法。学生可能会用手去度量，看看有几拃；也可能用尺子测量，看看具体有多长。此时教师应引导学生思考：这些度量工具有什么共同的特点？学生会发现，无论是手还是尺子，其实都是用线去量线。由此迁移过来，度量面积的大小，就应该是用面去量面。同理，这样的方法还可以迁移到体积的度量，从而帮助学生建立从一维到三维度量的结构性认知。

2.纵向贯通，疏通知识脉络

数学学科的每个知识点都不是独立存在的，我们总是能溯其源、寻其根。教师要带领学生贯通知识点的前后联系，让新知识纳入原有知识结构中同化。例如，教学人教版小学数学教材五年级上册“多边形的面积”时，教师就要对该单元的知识进行梳理（如图4），帮助学生厘清本单元的知识脉络。尤其是帮助学生体会单元的核心数学思想方法——转化，让学生明白，是转化的思想将单元的各个知识点串成线、结成网。此外，教师还要带领学生梳理、归纳转化的具体实施策略，包括割补法、剪拼法、分割法、等积变换等，以及各个面积公式的内在联系。从而实现平面几何图形面积知识体系的立体构建。

3.多向拓展，融通数学文化

数学体系庞大且繁杂，它除了自身内部关联紧密，还与其他学科，甚至与生活、文化都息息相关。《义务教育数学课程标准（2022年版）》明确提出，教师要关注数学学科发展前沿与数学文化，继承和弘扬中华优秀传统文化。为此，在数学教学中要把握知识的内外关联，适时渗透数学文化，让学生了解知识背后的相关历史，体会其承载的思想与文化，激发学生学习兴趣，提升学生文化素养。

例如，在教学人教版小学数学教材四年级上册“公顷和平方千米”时，教师给学生渗透中国传统的土地面积单位：亩、分、厘的相关知识。让学生了解人们常说的“一亩三分地”到底有多大，同时了解古代“井田制”的由来，及土地丈量单位的历史演化过程。在数学文化的学习中，提升学生的民族自豪感和文化自信。

（作者单位：浙江省温州市瓯海区南白象新生小学 江苏省扬州市育才小学）