深耕动静视角　迭代概念生长

［摘  要］ 研究者以教学“角的再认识”一课为例，通过“教材研读，明晰概念本质；学情分析，聚焦教学难点；单元整合，重构教学路径；课堂实践，深化概念教学”等策略开展教学实践，以动静视角整体构建角的概念，创设深度有序的教学活动。

［关键词］ 概念教学；角的概念；动静视角；单元视域

《义务教育数学课程标准（2022年版）》（以下简称“新课标”）将数学课程要培养的核心素养表述为“三会”：会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界。数学概念是数学思维的外显形式，是事物本质的语言表达，是形成新课标中“四基”（基础知识、基本技能、基本思想、基本活动经验）的核心。概念教学作为数学核心素养培养过程中的重要手段，是学生会用数学思维解决问题的重要工具。因此，新课标更关注学生对数学本质的把握，强调关注概念形成和发展的过程。

然而在概念教学过程中，部分教师常常忽略概念的形成过程，没有凸显概念本质，缺乏概念的结构性教学。比如在教学“角的认识”时，部分教师常常出现如下问题：只关注角的结构特征进行浅层教学，忽视角的概念的作用与价值的深度教学，导致学生对角的认知片面化；对教材中的两种静态、动态定义理解不深，导致学生对角的认识不够全面，从而在量角、画角环节出现偏差。教师应如何引导学生准确理解“角的概念”？笔者以“角的度量”单元为例开展单元整体教学研究，以“角的概念”为单元主线，明晰单元知识脉络。

一、教材研读，明晰概念本质

1. 教材横向对比

“角的度量”属于“空间与图形”板块中“测量”的内容。人教版教材分四个阶段对角的概念进行建构：第一阶段为“整体认知”阶段，二年级上册学生对角的认知属于整体认识，教材没有对角的概念给出明确定义，让学生通过观察、操作对角进行识别，从生活中的角抽象出数学中的角。第二阶段为“元素刻画”阶段，四年级上册是角的概念的正式呈现，静态定义出现在“线段、射线、直线”之后。借助静态角的定义“由一点引出两条射线所组成的图形叫作角”，就能解释“为什么角的大小跟两边的长度无关”。可见，角的大小立足于结合点线元素的静态角的概念，符合学生的认知发展逻辑。动态定义出现在“角的分类”一课中，此定义打破了静态定义的局限，是立足点线元素高度抽象角的概念。第三阶段为“动静关联”阶段，七年级学生对角的认识进一步拓展到图形元素的动静关联。第四阶段为“动态刻画”阶段，到了高中，学生则通过深入的动态刻画达成对角的概念的深化认识。

由此可见，学生对角的认知经历了从感性到理性、从静态到动态的递进过程。

2. 教材纵向梳理

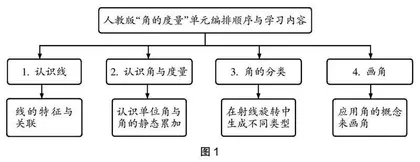
如图1所示，以动静结合的视角看本单元的序列，可以发现：第一课时认识线段、直线、射线，指向线的特征与关联；第二课时指向认识单位角与角的静态累加；第三课时指向射线旋转中生成不同类型的角；第四课时指向应用角的概念来画角。

可以看到，角的概念遍布于四个课例中，人教版对本单元的教学设计更偏向静态角的教学，然而这些知识点要以动态的眼光去审视。比如，角的分类是对动态识角的再运用，画角是对运用角的概念的动态刻画。因此，教师要基于“角的概念”研究“角的教学”，用数学概念指导后续的“量角”“画角”等教学活动，使教学活动更有结构性。

3. 不同教材对比

北师大版数学教材编排的是在旋转中认识角，且在旋转中形成不同类的角。对比两版教材的素材形式，人教版教材指向角的静态结构——射线组成的结果；北师大版教材指向角的动态结构——射线旋转的过程；两者都跟元素射线有关。值得教师思考的是：静态角或动态角切入，哪个更能建构角的概念，更能确保学生全面、深入地掌握角的概念？

教材虽然呈现了本单元角的概念教学的必要性，但是存在动态角的教学环节不够扎实的问题。因此，教师要引导学生以动静结合的视角对角的概念进行深度认知，为后续学习画角、量角等知识打下基础；要引导学生从小学阶段的静态角顺利过渡到中学的动态角；要从动静结合的视角对教材的单元序列进行重构。

二、学情分析，聚焦教学难点

在遵循学科逻辑的基础上，笔者为了精准把握学生对角的认知起点，基于角的概念的生长点和抑制点，设计了两类问题：对未学过本单元内容的学生设置了角的认知前测题，对学过本单元的四年级学生设置了操作类后测题。

前测访谈题：如图2所示，图中有角吗？你判断的依据是什么？

结果显示：约11%的学生处于关联结构水平，即能基于射线的旋转动态建构角，能与静态角的元素产生关联；约23%的学生处于多元结构水平，即能基于射线的旋转动态建构角，但不能与静态角的元素产生关联；约54%的学生处于单一结构水平，即能基于角的表象整体静态识别，能分解角的元素；约12%的学生处于前结构水平，只能基于角的表象整体识别，无法分解角的元素。由此可见，多数学生处于认知静态角的层面，无法识别由射线通过旋转所形成的动态角，如平角、周角等。

操作应用题：如图3所示，用量角器度量角的大小。

结果显示：量角错误率约29%，错因在于学生停留于对角的片面认识，如“射线与0刻度未重合”“角度数的反向读取”，这些错误都是由于学生缺乏对角的元素的动态感知。

在教学过程中，教师要利用静态角和动态角的关联，引导学生形成角的整体概念，这是为后续“量角”“画角”等内容提供正迁移的关键要点。

从教材解读和学情分析中可以得到启示：教师要引导学生结合点和线的元素，以动静结合的视角对角的概念进行建构。

三、单元整合，重构教学路径

1. 单元核心概念提炼

核心概念指向数学学科结构的主干部分，能反映学科对象本质关联的内容。本单元内容笔者以元素的运动为核心概念，以“在元素点、线的运动中认识不同的线，形成不同的角，并会度量和应用”为单元目标，以“点动成线、线动成角、旋转测量、动静关联、拼画实践”为整合路径重新编排教学内容（如图4所示），并达成如下教学目标：（1）认识线的特征与关系；（2）建立角的动、静概念；（3）掌握用单位角度量；（4）在旋转中画出不同类的角。教师引导学生整体建构角的认识、度量，对概念达成深度理解。

2. 单元核心内容重构

整合后的教学课时安排保证了教学的板块和结构不变，凸显了动静视角和整体感知的特点（如图5所示）。比如，第二课时补充了角的再认识这节课例，迁移点动成线到线动成角，建立角的动静概念；第三课时以主题活动“智创量角器”驱动课堂，让学生在创造量角器活动中体验单位角，学会度量角；第四课时整合画角和分类，让学生在画不同的角中，掌握角的分类与画法。

四、课堂实践，深化概念教学

基于上述分析，笔者围绕单元重构后的关键课例“角的再认识”进行例证。

1. 唤醒经验

（1）回顾经验

教师请学生回忆“角”长什么样子，并用手比画出样态。

教师出示若干个角，提问：什么是角？

预设：有一个顶点、两条边。

小结：由一个顶点、两条边组成的图形是角。

（2）概念重构

请学生思考：这两条边是什么线？

预设：射线。

请学生说：什么是角？

教师出示静态角的概念：由一个点引出的两条射线组成的图形是角。

2. 丰富概念

（1）任务启动

教师出示由一个点引出的一条射线，让学生思考：如果把这条射线绕着点动起来，这里有角吗？

活动1：动静关联——在动态中识角

活动要求：如果没角，请说明你的理由；如果有角，请用你喜欢的方法把看到的角都画出来。

（2）学情反馈

①层次1：辨析有无角

预设（没角）：只有一条射线。

预设（有角）：射线旋转过去会形成角。

学生分成没角和有角两大阵营，进行辩论。

教师追问：明明只有一条射线，另外一条射线怎么来的？

预设：射线旋转过去就产生了另一条射线，两条射线就形成了角。

教师再次追问认为没角的学生：现在你看到两条射线了吗？

总结：一条射线通过旋转到另一个位置，可以得到另一条射线，由此产生了角。

②层次2：理解射线在不同位置形成的不同的角

如图6所示，教师展示作品1（多个分开的角），让学生思考：他也认为有角，怎么看到了这么多角？

小结：射线通过旋转，能得到不同位置的第二条射线，就有了不一样的角。

如图7所示，教师展示作品2（刺猬图），让学生思考：你觉得有多少个角？这个角的两条射线在哪里？

小结：在旋转过程中，起始射线在不同位置，转到另一个位置得到射线，可以旋转出不同大小的角。

如图8所示，教师展示作品3（箭头图），让学生思考：你能看懂这个角的意思吗？箭头是什么意思？

小结：可以用这样的符号表示这条射线在旋转的过程中产生的所有角。

（3）对比概念

①层次1：形成动态概念

教师提问：现在你们对角有什么新的认识？

预设：一条射线旋转的过程也能形成角（请学生演示一条射线旋转形成角的过程）。

小结动态角的概念：角可以看作由一条射线绕着它的端点，从一个位置旋转到另一个位置所形成的图形。

②层次2：关注相同本质

教师提问：我们对角进行了两次描述，这两次描述有什么相同的地方？

预设：第二次描述中射线的一个位置到另一个位置就是第一次描述中的两条射线。

教师板书：沟通静态角的概念和动态角的概念的联系——两条射线的位置。

③层次3：寻找不同视角

教师提问：两种描述哪里不同？

小结：以前我们是用静的眼光看角，现在是从动的视角去看角，今后我们也可以学会用动的视角看世界。今天我们就从动静结合的视角对角进行再认识。

3. 深化概念

（1）任务启动

教师提问：刚才通过旋转这条射线到另一个位置，出现另一条射线，形成了角。如果继续绕这个点旋转，还会出现怎样的角？你能转出一个与众不同的角吗？

活动二：动中取静——在特殊中辨角

活动要求：画一个与众不同的角，说一说它哪里与众不同。

（2）学情反馈

①层次1：锐角、直角、钝角

概念判断：如图9所示，它们是角吗？怎么得到的？

预设（静态角视角）：都有一个顶点和两条射线。

教师追问：从静态的视角看是有两条射线，从动态的视角看是怎么得到的？

预设：一条射线从起始位置转到这里为止（手势）。

预设（动态角视角）：这条射线从一个位置转到另一个位置，得到了两条射线。

教师追问：（个性判断）它们不同在哪里？

预设：旋转时转过的程度不一样。转过程度比较小的是锐角，第二个是直角，比直角大的是钝角。

②层次2：平角

概念判断：如图10所示，它是角吗？

学生分成两个阵营进行辨析。

预设（不是角）：不是，只有一条线。

预设（是角）：是，一条射线转到对面。

教师提问：它的第二条射线是怎么得到的？

生：通过旋转射线到相对位置，形成平平的样子。

对比作品：如图11所示，这两种画法你更喜欢哪一种？

预设：第二种，能让人一眼看清楚这条射线是怎么旋转后得到第二条射线的。

教师提问：（个性判断）这个角与众不同在哪里？

预设：这条射线转到和它相反的位置，形成了这个角。

小结：一条射线绕着端点旋转到与它相反位置形成的角是平角。