策略教学：三“思”而行

［摘  要］ “解决问题的策略”的教学可以从三个方面进行思考：在改编和回顾中思考联系，帮助学生形成知识体系；在对比和变式中思辨内化，帮助学生把握策略本质；在活动和反思中思量方法，帮助学生掌握知识背后的数学思想。

［关键词］ 策略；知识体系；数学思想苏教版小学数学教材有一个特点：从三年级开始，每册课本都安排了一个重要的学习单元“解决问题的策略”，主要是针对某种特定类型的问题，让学生对问题中的数量关系进行分析，通过探究找到最优化的解决方法。

学生在数学学习的过程中会遇到各式各样的数学实际问题，在解决这些问题的过程中会逐步积累解决问题的经验。“解决问题的策略”这类课的价值在于培养学生的“策略意识”，让学生有意识地运用策略来解决数学问题，发展学生的数学思维。

笔者以“用一一列举的策略解决问题”（下文简称“一一列举”）一课为例，谈谈对“解决问题的策略”教学的一些思考。

一、思考联系：整合成体系，回顾再建构

小学数学是一个完整的知识体系，“解决问题的策略”这类课虽然每一节课教学的侧重点不同，但是教师在教学设计时要有整体意识，让学生的思维不能停留在本节课的几道数学习题上，更要关注所学知识和方法之间的联系。教师应引导学生既要关注本节课学习的策略，还要思考与学习过的其他策略之间的联系；既要关注本节课解决的实际问题，还要联系解决过的实际问题蕴含的策略，进而体会策略运用的广泛性。

1. 恰当改编，整合策略

在解决数学问题时可能用到不止一种策略，从不同的角度出发会用到不同的策略来解决同样的问题。教师在设计教学内容时，要从学生的“最近发展区”出发，关注知识和方法之间的联结，让学生的思维更加系统化。教师可以将例题、练习进行适当改编，将策略进行整合，往往能取得较好的教学效果。

“一一列举”这一课原来的例题为：“王大叔用22根1米长的木条围一个长方形花圃，怎样围面积最大？”在教学时，教师常常会让学生从条件出发，通过文字描述、画图、列表等方式进行一一列举，从而得出结论。

教师可以将例题改编为：“王大叔用22根1米长的木条围一个长方形花圃，围成的花圃面积可能是20平方米吗？”改编后的例题便于学生从两个角度进行思考。

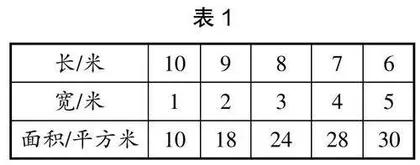
第一种思路：从条件“周长是22米”出发进行一一列举，并绘制表格（如表1）。

表1

学生对表中的数据进行比较和分析，发现不能围成面积是20平方米的花圃。学生运用一一列举的方法进行有序列举，运用“从条件出发”的策略进行思考。这样，学生在解决问题的过程中能感受策略之间相辅相成的关系，为解决问题提供方法上的指引。

第二种思路：运用“从问题出发”的策略思考问题，从问题“面积是20平方米”出发进行一一列举，看看周长能否是22米，并绘制表格（如表2）。

表2

学生对表中的数据进行分析，同样得出“不能围成面积为20平方米的花圃”的结论。

因此，教师通过对例题进行恰当的改编，给予学生更多思考的空间，让学生从不同角度思考问题，能在一定程度上拓展学生思维的宽度，让学生感受策略之间的联系，从而让策略教学最终形成体系。

2. 联系旧知，再建策略

在例题教学后，教师可以引导学生想一想以前解决问题时应用过的“一一列举”策略，让学生经历从“似曾相识”到“恍然大悟”的过程，这有助于加深学生对策略的理解和策略模型的建构。

在教学“一一列举”例题后，教师可以安排小组活动：“回忆一下我们曾经运用一一列举的策略解决过哪些问题？”学生经过回忆和交流，清晰地说出一些解决过的问题，比如用3张卡片组成的三位数、用12个边长1厘米的正方形拼成周长不同的长方形等。教师引导学生简单回顾解决此类问题的过程，感受有序列举的方法。

简单的回顾架起了学生已有经验和新知识之间的桥梁，让学生明白策略学习可以解决遇到的数学问题，在不知不觉中提高了运用策略的意识。

二、思辨内化：思辨起冲突，对比显本质

“解决问题的策略”教学的实质是借助策略帮助学生寻求合适的解决问题的途径。学生在合作探究和全班交流的过程中，通过对比能感悟最方便的解决方法并加以应用。对比和变式练习是让学生把握知识本质常用的方法，通过对比选择更优化的方法，通过思辨能“知其然并知其所以然”。

1. 题组对比，把握本质

当学生掌握如何运用策略解决问题之后，教师要引导学生感悟该策略的适用范围，这是“解决问题的策略”教学的重点之一。

在教学“一一列举”例题之后，笔者出示这样的题组（如表3）。

表3

在学生初步学会运用策略解决问题后，教师以题组的形式出示练习题，让学生在对比中辨别、把握策略的本质，让学生不仅知道怎样解决问题，还能判断什么样的问题适合运用该策略来解决。与此同时，教师将旧知识穿插在题组中，让学生感受策略运用的广泛性，进一步增加学生对策略的“好感”和兴趣。

2. 方法优化，灵活运用

学生不仅要学会借助策略来解决问题，还要通过对比灵活选择更为便捷的方法来解决问题。在练习中，教师可以设计一些相关类型的实际问题，体现问题解决方法的多样性，让学生通过对比找到更优化的解决方法，提升灵活运用策略的能力。

在“一一列举”一课中，笔者设计了练习题（如表4）。

表4

学生直接列举有些困难，不容易列举齐全。教师可先让学生自己尝试练习，再进行小组交流。学生先对不同列举方法进行对比，再将此类问题的解决方法进行优化，即将代金券先按照张数进行分类，再有序进行一一列举。这样不仅让学生的思路更加清晰，而且让他们知道在遇到实际问题时要学会灵活运用策略。

三、思量方法：活动里渗透，反思中明朗

数学思想方法蕴含在解决问题的过程中，学生一方面要在实际操作中感受和概括数学思想方法，另一方面要自觉运用思想方法解决实际问题。教学中，教师要引导学生关注解决问题蕴含的数学思想方法。

数学思想方法的学习过程一般需要经过“操作渗透—总结归纳—灵活运用”三个阶段，在设计教学环节时，教师要关注每个环节知识背后的思想方法。

1. 创设活动，渗透方法

学生对思想方法的领悟可以通过数学活动来实现。首先，教师要创设恰当的活动和提出清晰的活动要求；其次，教师在课堂中要给学生营造一种宽松的活动环境，让学生可以自由活动；最后，在进行活动交流时教师要允许学生畅谈自己的想法，在学生求解的基础上进行引导和总结，使学生感受问题背后的数学思想方法。

在教学“一一列举”时，首先，笔者让学生通过仔细读例题，说说其中的条件和问题，在此基础上设计了本节课的第一个活动：通过画一画、写一写、列一列等方式尝试解决问题（遇到困难时可以借助小棒摆一摆）。在活动中笔者既给予学生一定的方法指引，又赋予足够的空间让学生自主尝试，使其在解题的过程中感受蕴含的数学思想方法。其次，笔者让学生在小组中交流自己的做法，这是从自主探索到小组互学的过程，也是学生在自学的基础上带着自己的认知和感悟进行二次思考。最后，小组选派代表在全班进行展示，这是学生的第三次思考。在这期间，笔者适时进行点拨，让学生在充分思考的基础上认识和理解解题过程中蕴含的数学思想方法。

当学生说到可以将“长方形的周长是22米”转化成“长+宽=11米”进行思考时，教师适时点拨：“这位同学很有数学智慧，在数学上这是一种化繁为简的数学思想。”当小组展示画示意图、文字列举、列算式等方法时，教师引导学生比较这几种方法：“这几种方法有什么共同的地方呢？是的，他们都是按顺序进行列举的，这体现了一种有序的数学思想。”通过不同思路的比较，能让学生感受解决问题方法的多样性。

2. 反思练习，建构方法

日常教学中，有些教师认为新课要精讲，练习只是辅助可以略讲，这是不对的。练习是对知识的巩固，能让学生感悟习题中所蕴含的各种思想方法。教师在备课时要重视练习的设计，不仅要重视知识层次上的设计，还要重视学生对思想方法的习得。

在“一一列举”一课的练习中，笔者设计了练习题（如表5）。

表5

在学生解决问题的过程中，教师边巡视边表扬一些学生解题速度快：“我很想知道为什么有些同学解题的速度非常快，请他们上台展示一下自己的方法。”通过展示发现，有的学生是用简写的方式（比如将西红柿简写为西），有的学生使用数字或字母的方法（比如将蔬菜用A、B、C来表示，水果用1、2来表示），有的学生用图形来表示蔬菜和水果的名称。这些方法提高了书写的速度，这是一种符号化的数学思想。

总之，在设计“解决问题的策略”一类课时，教师要从发展学生的思维出发，对教学内容、教学方式和背后的思想方法进行深度思考，精心设计教学活动，让学生的学习真正发生。