“学讲方式”背景下的小学数学结构化教学评价研究

［摘  要］ 研究者以“多边形的面积整理与联系”的复习教学为例，从“自主整理知识，建构知识体系”“设计多层练习，巩固知识技能”“提炼数学思想，凸显学科育人”三个方面开展教学与分析，探索“学讲方式”背景下的小学数学结构化教学评价研究。

［关键词］ 学讲方式；结构化；教学

“学讲方式”是一种将自主先学、合作互助与交流反馈作为核心理念的教学方法，“学进去”与“讲出来”是这种教学方式的基本要求。教师将结构化教学与学讲方式有机融合在一起，不仅能让学生在导学案的引导下高质量完成教学目标，还能有效发展学生的整体思想，增强学生的自主学习能力与结构意识。这是践行《义务教育数学课程标准（2022年版）》（以下简称新课标）倡导的“以生为本”与“结构化”教学理念的基础，也是发展学生数学核心素养的重要渠道。

一、“学讲方式”下结构化教学评价分析

切实可行的评价标准是践行“学讲方式”教学的关键，也是实施结构化教学的核心。教师根据学情与知识特点设计贴近学生认知的教学活动与评价标准，既能有效规避教师“居高临下”地管理课堂，又能激发学生的学习热情。结合学讲方式与结构化教学的特征，教师可以从“自主、合作、展示、参与”等方面设定相应的评价指标，明确自身在教学中的权重。

1. 自主

教师根据学生的实际情况与知识特点拟定课前自学提纲，引导学生自主完成相应的预习任务，为课堂教学奠定基础。教师在此环节的权重约占25%左右。

2. 合作

教师引导学生以小组为单位进行合作交流，并营造良好的学习氛围，让学生在合作过程中通过质疑与释疑对某些问题达成共识，然后教师在必要时参与探讨、点拨与评价。教师在此环节的权重约占25%。

3. 展示

教师将学生合作交流的成果进行板书或投影展示，引导学生从正确的示范中发展数学思维。教师在此过程中的权重约占45%；

4. 参与

教师引导学生有序参与数学活动，通过师生、生生双边积极的互助完成学习目标。教师在此环节的权重约占25%。

当然，这只是针对“学讲方式”下的结构化教学所提出的抽象性建议，在具体实施时教师要根据实际情况进行调整。课前，教师可以给每个小组发放一张自主学习任务清单，明确合格、良好、优秀的评价标准，让学生从参与程度、交流质量等方面判断参与效果。学生个人的评价结果与小组成绩直接挂钩，做到组内成员荣辱与共。

下面，笔者以“多边形的面积整理与联系”的复习教学为例，探讨“学讲方式”背景下的小学数学结构化教学的评价研究。

二、具体措施

1. 教学分析

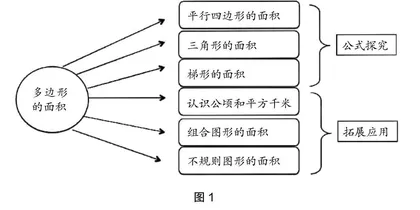
如图1，“多边形的面积”单元主要包含了平行四边形的面积、三角形的面积、梯形的面积、认识公顷与平方千米、组合图形的面积以及不规则图形的面积六个方面的内容。前三项属于公式探究，后三项属于公式的拓展应用。本节课为复习课型，学生通过以前的学习掌握了用图形的拼接、平移与旋转等方法研究不同平面图形的面积公式以及计算面积的方法，能借助相应的经验解决一些与图形相关的面积问题。

2. 教学简录

（1）拟定教学提纲，展现自学能力

认知结构理论提出：想要掌握所研究事物的结构，最好的方法就是用大量与之相关的事物与它联系起来进行分析与理解。数学知识的学习要达到理解与灵活应用的程度，最好的方法就是学习者在头脑中建构一幅以核心知识为载体的知识结构图。多边形的面积计算问题涉及各类图形面积公式，其中很多内容具有一定的联系性，可以互相转化。在本节课上课之前，教师可结合自身的教学经验与知识结构特点拟定教学提纲，让学生自主完成，以更好地了解学情，为接下来的教学奠定基础。

（2）深入合作探索，建构知识体系

合作探究是“学讲方式”模式的重中之重。学生在旧知回顾阶段，重点并不在于计算公式，而是厘清多边形计算公式间的联系，将原本零散的知识有机整合在一起，形成具有一定关联性、生长性与连续性的知识结构图，这是重建知识体系的关键。想要达成这一目标，教师可以从知识的横向与纵向联系出发引导学生开展合作探究。

①横向关联，串联知识点

在自主梳理知识点的同时，教师可引导学生从横向关联的角度将各部分知识有机地串联起来（学进去），用恰当的数学符号语言进行描述（讲出来），以便更好地理解与记忆相应的公式，并对原有的知识达到更深层次的理解。学生通过自主梳理过程形成各种体验与感悟，这些都是积累学习经验的过程。

在知识点整理教学时，教师要以点拨的方式引导学生将本单元所接触的平面图形公式一一回忆，罗列在草稿本上，并思考问题：“若让你从这些公式中择取一个图形的面积公式作为推导其他图形面积公式的基础，你会选择哪个公式？请选择一个公式并写出具体的推导过程。”

大部分学生以“从简单到复杂”的方式整理并书写推导过程。如图2，教师将学生整理的结果进行归纳，由左向右观察，知识的形成与发展过程一览无遗；从右向左观察，发现本章节的知识具有互相转化、和谐统一的特征。

②纵向关联，盘活知识链

在“多边形面积”的横向结构整理的基础上，教师以学生已有认知经验为教学的生长点，鼓励学生换一个思维角度，以其他图形作为知识结构整理的出发点探寻各个知识点间的联系。

在这个问题的引导下，学生分别以梯形、平行四边形、三角形的面积公式作为思维的基础逐一开展分析。

第一步：以梯形的面积公式作为思维的基础开展分析。

教师引导学生开展丰富的想象、思考：缩短梯形的上底a，在下底b与高h不变的情况下，梯形最终会变成一个什么图形？学生自主画图分析，很快就获得“梯形→三角形面积的公式的推导过程”，即S=（a+b）·h÷2→S=（a+0）·h÷2=a·h÷2（三角形面积）。

如果将梯形的上底进行延长，使上底、下底的长度相等，在高不变的情况下，梯形会变成什么图形？学生通过画图分析，获得“梯形→长方形或平行四边形的公式推导过程”，具体过程为：S=（a+b）·h÷2→S=（a+a）·h÷2=a·h。

此过程，学生通过自主画图与思考，发现三角形、平行四边形以及长方形的面积公式均可由梯形的面积公式推导而来。

第二步：以平行四边形的面积公式作为思维的基础开展分析。

借助《九章算术》中与多边形面积相关的内容，教师引导学生以小组合作学习的方式开展分析。此过程不仅起到渗透数学文化的作用，还让学生通过剪拼法，感知用平行四边形面积公式推导其他图形面积公式的具体过程，对多边形面积转化原理做到“知其然且知其所以然”。

操作完毕，各组展示探索结论：如图3，以平行四边形的面积S=a·h为出发点，通过不同的剪拼法，分别获得三角形的面积为S=a·h÷2，梯形的面积为S=（a+b）·h÷2。

第三步：以三角形的面积公式作为思维的基础开展分析。

如图4，三角形作为基础图形，通过对其的转化，可以分别推导出平行四边形与梯形的面积公式。同样，此过程以“讲学方式”为基础，教师要引导学生在理解与表达的基础上借助思维导图的方式展示结论。

以上三种探究方式对小学生而言，实属不易。基于合作交流的模式进行探索，不仅让学生自主将不同图形的面积公式联系到一起思考，还让学生进一步感知知识与知识间密不可分的联系，很多内容间可以互相转化。在推导过程中，教师借助多媒体进行展示，能让学生一目了然地了解公式推导的来龙去脉，在理解的基础上完善知识结构和发展学力。

（3）设计多层练习，参与巩固技能

学讲方式背景下的教学离不开练习训练的辅助，教师要基于结构化的视角设计练习，要从整体性的角度出发，考虑知识的关联性，设计具有针对性、连续性、层次性、拓展性等特征的问题，进一步加强学生的参与度，达到查漏补缺的目的。

本节课，笔者结合学情与复习内容的特点，引导学生用基本图形面积研究经验来解决一些生活实际问题。此外，笔者还通过题组练习进一步拓宽学生的思路，完善学生的认知，促进学生的深度学习。

问题1：已知梯形的两个底长的和为25厘米，高为5厘米，该梯形的面积是多少？

问题2：如图5，已知图中阴影部分正方形的周长为16厘米，那么图中平行四边形的面积是多少？

问题3：观察图6中甲乙两部分面积，谁更大一些？

这组练习引导学生将多边形的面积公式联系在一起进行分析与整合，使学生的思维随着练习应用获得二次发展。这样不仅进一步完善了学生的认知体系，还让学生在积极参与中发展了数学思维，引起了学生对各种面积公式的思辨，让复习变得更加高效，让学生的认知结构更加完整。

（4）提炼数学思想，凸显学科育人

数学思想是指学习者对数学本质的理解，是知识与方法之上更高层次的抽象，对学生个体的成长具有深远的影响。新课标将数学思想置于重要地位，让其成为数学教育的重要组成部分。因此，学讲方式背景下的结构化教学中，教师既要关注显性的知识与技能、研究方法的探索，还要关注学生数学思想的提炼。只有挖掘出隐藏在知识背后的数学思想，才能从真正意义上凸显教学价值，这是发展学生数学核心素养的必经之路。

数学思想的提炼需要经历复杂的过程，教师要引导学生经历操作体验、灵活应用以及联系发展等阶段，发挥结构化教学的优势。本节课，学生从不同的视角推导多边形面积公式时，涉及了数学一般化与模式化的过程，“转化思想”贯穿教学的始终。

思想方法对处理数学问题具有指导作用，学生的数学思想方法的形成离不开大量样例的辅助。本节课，学生在转化思想这条暗线的指导下，不断积累活动经验和提升感悟，促使课堂从知识立意转向能力立意，实现了育人功能。

总之，“学讲方式”背景下的结构化教学时，教师应将知识点的统整与知识体系的重建放在首位，以上串下联的方式设计层次清晰的练习，引导学生形成结构化的知识体系，发展学生数学核心素养。