数学教学中培养学生隐性学力的实践与研究

［摘  要］ 教师应培养学生的隐性学力：以充满活力的活动设计指引，培养学生的意志力；以教材本身的核心内容为载体，培养学生的思维力；以勇于质疑和善于反思为目标，培养学生的批判力；以创意改编例习题为途径，培养学生的研创力。

［关键词］ 隐性学力；数学教学；数学思维

钟启泉教授认为，学力是认知、理解、技能、思考力、判断力、动机和态度的总称，小学生的学力可分为“显性学力”与“隐性学力”两大重要组成部分。“显性学力”是指知识技能、理解与记忆等，是知识与技能层面的习得结果；“隐性学力”是指意志力、思考力、体验力、批判力、研究力、创造力等，是知识与技能背后的学习方法、思维方式、情感态度与价值观。实践表明，学习者的显性学力在总体学力中只占很小一部分，而真正影响学力发展、决定学力走向的是隐性学力，隐性学力是促进学生综合学力发展的有力支点。在数学课堂中培养学生的隐性学力，是教师义不容辞的责任。

一、以充满活力的活动设计为指引，培养学生的意志力

意志力是学习者自觉确定目标，从目标本身出发支配和调节行动，并克服重重困难达成目标的品质。学生拥有良好的意志力，就能迎难而上，努力克服数学学习中的一个又一个困难，攀登数学学习的一个又一个高峰，建立学习数学的自信心。“钢铁般的意志比智慧、博学更加重要”，培养学生的意志力十分重要。教师在教学中可以用趣味性导入激发学生的学习兴趣，用探究性活动撬动学生的思维，让学生在解决“障碍”的过程中体验成功的愉悦，自然地培养学生的意志力。

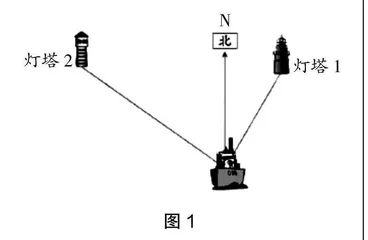
案例1  用方向和距离确定位置

问题导入：海上有一艘遭遇故障的轮船在等待救援，救援人员需要知道哪些信息？（学生畅所欲言，认为需要知道方位与距离岸边的距离）

师：如图1，可以根据灯塔位置来确定吗？（学生观察后各抒己见，认为在灯塔1的西南方向）

师：他们这样的描述有什么不足之处？（学生窃窃私语）

生1：他们描述的方向区域很大，轮船与灯塔的位置关系没有说得特别清晰。

生2：就算他们说了准确的位置关系，救援人员找到遇险轮船也要花费好多时间。

师：为什么？

生3：我觉得要讲清楚轮船与灯塔1或灯塔2间的距离。

师：的确如此，想要在最短时间内搜救，不仅方向要清晰，而且距离要清晰。仅凭图1可以解决这些问题吗？（学生沉默）

师：如果你在轮船上，这么多人的生命都掌握在你手中，此时需要冷静，需要具有迎难而上的勇气。所以，我们现在冷静下来思考一下：以上两个问题你能解决到什么程度呢？倘若想要让问题获解，你需要什么帮助？（在教师言语和眼神的激励下，学生开始小声探讨）

生4：其实我们现在说的只是一个大概方位，如果使用量角器，是不是就可以得到清楚准确的方向呢？（说着取出量角器）

生5：借助直尺，是不是可以量出轮船和灯塔1或灯塔2间的距离呢？（取出直尺跃跃欲试）

生6：用直尺度量的是图上的距离，现在求的是实际距离，我们还需要知道比例尺！

教师引导学生在解决困难的过程中接受思维和意志的历练，进而提升意志力。以上案例中，教师精设探究性活动，激起学生的探学热情，引发学生的愤悱之情。在学生意志逐渐减弱的时候，教师适时激励与点拨，让学生以更大的热情与思维投入探究活动中，努力地“跳一跳、摘果实”，既解决问题又培养意志力。

二、以教材本身的核心内容为载体，培养学生的思维力

教材是教师教学的依据，教师唯有创造性地运用数学教材，才能让学生受益匪浅，真正意义上发展学生的思维力。在学科教学时，教师要重视对学生思维力的培养，以教材本身的核心内容为载体，通过基于学生思维特征的教学设计，引导学生进行自主探索，让学生在思维活动中习得知识，在反复应用中内化知识，从而促进思维力的发展。

案例2  分数的初步认识（二）

师：大家看，图中是什么？（课件出示盘子装有1个桃的图片）

生（齐）：1个桃。

师：平均分给2只猴子，每只猴子可以分得多少？

生1：半个。

师：每只猴子分得的是这个桃的几分之几？

生2：。

师：它们各分得这个桃的，也是个桃，对吗？

生（齐）：对！

师：现在是4个桃，将这盘桃平均分给2只猴子。

生3：各分得2个桃，各分得这盘桃的。

师：为什么每只猴子分得的是这盘桃的？

生4：这盘桃平均分成2份，1只猴子分得其中1份，那就是分得这盘桃的。

师：生4的意思是将这盘桃看作一个整体，将其分成2份，这样每只猴子分得其中的1份，所以仍然用表示，其他同学觉得对吗？

生（齐）：对！

师：再来看，现在这盘桃有6个。

师：你们能表示它的吗？（学生先自主画图，然后进行讨论，认为“一盘桃就是一个整体，平均分为2份，涂色部分是其中1份”）

师（追问）：这盘桃的是几个？

生（齐）：3个。

师：继续看，现在这盘桃有10个。

师：如何表示它的？这盘桃的是几个？（学生自主画图，小声讨论并得出结论）

师：这里每盘桃都被平均分成了2份，每1份有几个？（课件出示分别装有4个、6个、10个桃子的图片，学生进行回顾并描述）

师：每1份桃的个数各不相同，都用表示，为什么？

生5：不管一盘桃的个数是多少，它都是一个整体。

学生思维力的培养应贯穿数学课堂教学的全过程，教师要用良好的导入开拓学生的思维路径，用逐渐深化的内容拓展学生思维广度、深度，让学生的思维更具灵活性、新颖性、独创性和抽象性。以上教学过程，教师基于教学内容本身采用渐进式教学模式，让学生充分认识“桃的总数无论如何变化，都是将其平均分成2份，虽然每1份桃的个数随之变化，但是将一个整体平均分成2份，每1份依旧是整体的”，切实感受从具体的个数抽象为整体“1”的过程，从而完成从特殊到一般的抽象，发展学生的数学抽象思维。

三、以勇于质疑和善于反思为目标，培养学生的批判力

实际教学中，教师往往重视培养学生的思维力和创造力，忽视培养学生的批判力，这显然是不当的。事实上，学生如果没有批判就没有质疑和想象，也就没有数学能力。因此，培养学生的批判力不容忽视。教师要从教学内容的特征出发，鼓励学生勇于质疑和善于反思，培养学生的批判性思维。

案例3  面积的认识

师：如图2，①和②的面积哪个大？

生1：我觉得②的面积大。

生2：我觉得差不多大。

师：看是看不出的，该怎么做呢？

生3：分别把它们剪出来，然后重叠比较，如何？

师：听着似乎可以，我们试一试？（学生分组实践，发现无法比较）

师：那我们得另辟蹊径了！大家看，怎么利用这个方格纸？（学生进行探讨）

师：将剪好的长方形放在方格纸上，分别数出它们占有的方格数。（学生开始试着操作，并得到结果）

师：现在回想一下，我们比较两个图形面积的大小有哪些方法？（学生七嘴八舌地说出观察法、重叠法、数方格法）

师：可有疑问？

生4：假如这个图形不是刚好铺满整格，该怎么办？

师：哇！真是具有质疑意识的好孩子！会这样吗？哪些时候会这样？这样的情况该怎么处理？

生5：图中的两个图形都刚好铺满格子，但只要变化任何一个图形的长或宽，就会出现这样的情况。

生6：其实很简单，若是不规则图形肯定会出现上述情况，比如两片树叶。（教师适时呈现学生描述的无法铺满整格的长方形及一个不规则图形）

师：你们所提的问题具有非常大的探究价值，下面就让我们一起深入研究。

在教学中，教师如果止步于几种常见面积比较的方法，则很难发展学生的质疑精神和批判力。教师要鼓励学生进行回顾和反思，让学生自主提出疑问和困惑，并进行深入的思考与探索。在此过程中，教师引导学生加深对面积比较方法的感悟，自然地发展学生的质疑能力和批判性思维。

四、以创意改编例习题为途径，培养学生的研创力

在数学教学中教师引导学生开展探究活动是培养学生探究力与创造力的常规方法，更是发展学生数学核心素养的必要条件。基于这样的认识，教师可以通过挖掘、改编例习题，引导学生去观察、实验和探索，使学生获取知识技能，更好地培养学生研创力。

案例4  圆柱的表面积和体积计算

“已知圆柱容器底面半径与高，求制作容器需要多少铁皮及容器容积”这一类良性结构的问题过多，使得学生逐步丧失探究的积极性。基于此，笔者从问题本身的实践性与探究性出发创造性地改造习题，意在提高学生的研创力。

问题：已知图3所示的是几种不同型号的铁皮。

（1）用（  ）（  ）铁皮搭配，可制作一个无盖圆柱形水桶，请说明理由，并计算制作的水桶容积；

（2）王师傅选择铁皮A和D，可以制作一个有盖的水桶吗？如果可以，请说明制作方法；

（3）若用铁皮D加工一个容积为502.4升的圆柱形水桶，还需搭配一个什么样的铁皮？

事实上，学生的创造力不可低估，他们在数学探究中所收获的不仅是独立探求的能力，还有积极的情感体验、价值观及创造力。以上案例中，教师通过改编习题，融入多个不同形式的活动，让学生充分体验知识与方法的应用性，促进研创力的自然发展。

总之，教师既要重视提升学生的显性学力，又要重视发展学生的意志力、思维力、批判力、研创力等隐性学力。唯有二者相得益彰，才能真正发展学生的综合学力，增强学生的数学核心素养。