利用课后反思　提升教学品质

［摘  要］ 在实际教学中，教师不仅要备好课、上好课，还要及时进行课后反思，从而通过反思发现教学中存在的不足，不断改进和完善教学流程，以此提升教学品质，提高教学有效性。

［关键词］ 课后反思；教学品质；教学有效性

笔者在教学“图形中的规律”时，课前做了充分的准备，但是教学效果并没有达到预期。课后及时与教研组同事进行研讨和分析，找到了问题的症结，在第二次设计时基于第一次设计中存在的问题进行了有效的调整，取得了较好的教学效果，现将两次教学设计过程呈现给大家，以期共鉴。

一、第一次教学流程

本节课的教学目标是通过直观操作图形，引导学生多角度观察，发现蕴含在图形中的规律，体验探究的方式和方法，培养学生动手操作能力、分析能力和抽象概况能力。为了达成这一教学目标，在教学中教师要带领学生经历观察、列表、发现、交流、概况等活动，以此发现图形中的规律，并建立起数学模型。笔者结合教材内容和具体学情开始了第一次试讲。

1. 复习旧知，引入新课

师：学习新知前先考考大家，以下找规律填数字的问题你会吗？（教师用PPT展示题目）

（1）3、5、7、9、（  ）……

（2）3、6、9、12、（  ）……

（3）4、8、12、16、（  ）……

（学生答，略）

师：其实不仅数列存在着一定的规律，图形也存在着一定的规律，你们想不想探个究竟呢？

设计意图：从学生的已有知识和已有经验出发，呈现数的排列规律，以此激发学生探究图形规律的热情。

2. 设置游戏，引导探究

师：以上问题看来都难不倒大家了，接下来我们一起来玩一个闯关游戏，你们有没有信心通关？（听说是闯关游戏，学生探索的热情被激发了）

（1）第一关：火眼金睛

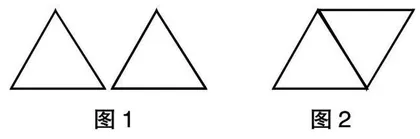
师：看一看，找一找，图1和图2有哪些相同点和不同点？（教师用PPT展示）

生1：相同点为图1和图2都有2个三角形；不同点为图1中的2个三角形是独立的，而图2中的2个三角形是连在一起的。

师：很好，还有其他发现吗？

生2：摆出图1中的2个三角形需要6根小棒，而摆出图2中的2个三角形只需要5根小棒。

师：观察得非常仔细，说一说为什么可以少用1根小棒呢？

生2：因为这2个三角形共用了1条边。

师：很好，如果让你给这条边起个名字，你想叫它什么呢？

生3：共用边。

师：很好，非常生动形象。数学中我们将这条边称为公共边。现在谁来具体描述一下，为什么少了1条边呢？

生4：因为图2中有1条公共边，所以图2比图1少用了1根小棒。

师：恭喜大家，顺利通过第一关。

设计意图：通过观察，分析两图中的异同，从而引出“公共边”，为接下来探究图形规律做铺垫。

（2）第二关：我摆你填

师：仿照图2的摆法，若想摆出10个三角形，需要用多少根小棒呢？请两人合作摆一摆，并完成表1。（摆一个，填一个）

学生积极实验，教师巡视，投影展示学生的统计表。

师：观察表1，你有什么发现？

生4：每多摆1个三角形需要添加2根小棒。

师：很好，现在我们重新演示一下实验过程，看看与你的操作过程是否一致。（教师一边摆、一边说，带领学生再次感悟生4的结论）

师：接下来请同学们结合表1读一读、说一说，摆出以上图形有几个公共边，需要几根小棒。

师：恭喜大家，通过合作顺利完成第二关。接下来的两个关卡很复杂，你们有信心继续闯关吗？（活跃课堂氛围）

设计意图：通过观察、实验、分析等活动引导学生经历发现规律的过程，体验发现图形规律的方法。此环节以合作探究为主，重在培养学生合作意识，提升学生学习品质。

（3）第三关：智慧比拼

师：接下来我们来个智慧大比拼，我说三角形个数，你们给出需要的小棒数量，看看谁说得又快又准。

师：如果按照图2的摆法，摆2个三角形需要几根小棒？

生5：5根。（学生抢答）

师：摆4个呢？6个呢？

学生积极抢答。

师：现在将表1增加一列（如表2），你会写吗？

问题给出后，学生一时不知从何写起，教师及时指导。

师：大家不要着急，一个一个来，先思考一下，摆2个三角形，算式是什么呢？

学生齐声答：3+2。

师：摆3个三角形呢？

生6：3+2×2。

师：很好，对于，其中“3”表示什么？2个“2”又分别表示什么呢？

生7：“3”代表第一个基础图形，2个“2”中一个表示每增加1个三角形需要添加2根小棒，另一个代表在基础图形的基础上增加了2个三角形。

师：说得很好，那么如果现在要摆100个呢？

生8：3+2×（100-1）。

师：如果要摆n个呢？

生9：3+2（n-1）。

在教师的引领下，学生抽象出了数学模型，接下来教师又给出了相应的练习让学生独立完成，学生顺利通关。

设计意图：通过由浅入深的问题引领，引导学生认清问题的本质，抽象出数学模型。

（4）第四关：神机妙算

师：如果将三角形变为正方形，你又能得到什么？

学生通过动手操作发现了规律，得到如果要摆n个正方形，则需要4+3（n-1）根小棒。

师：如果是n个m边形呢？

有了前面的积累和铺垫，学生顺利得出如果要摆n个m边形，则需要m+（m-1）（n-1）根小棒。

设计意图：通过由特殊到一般的转化，培养学生数学分析、数学抽象等能力和素养。

3. 拓展延伸，锻炼能力

在此环节，教师为学生准备了两道思考题：

问题1：如果把这些连续的多边形拆开，摆出如图1所示的图形，现在我们需要添加多少根小棒呢？

问题2：如图3所示，用若干2cm小棒摆出一些平行四边形和三角形，将其拼成1个大的平行四边形。已知大平行四边形的周长为244cm，那么这个大平行四边形中有几个小平行四边形？几个三角形呢？

设计意图：通过有效的拓展发散学生的思维，培养学生举一反三的能力。

4. 课堂小结，反思回顾

略。

通过让学生开展观察、操作、思考、交流等活动，笔者基本完成了本节课的教学任务，但是从学生的反馈和后期学生的参与热情来看，并没有达到预期效果，尤其到拓展延伸环节时，有些学生已经跟不上教师的节奏，可见学生的思维并没有完全得到发散。

二、课后研讨

课后笔者回顾教学过程并与同行交流发现，之所以课堂上出现这样的情况，是因为在教学中给定了基本图形这一概念，学生的思路局限在先摆1个多边形，每添加n-1根小棒，多边形就增加了1个。然而拓展延伸环节的问题打破了原有的思维路径，所以很多学生就感觉不知所措，从而陷入迷茫。基于此，教学中教师为何不让学生自己发现规律呢？为何不选择放手，充分发挥学生思维灵活性、多样性的特点呢？要知道，若学生一直被教师牵着走，则他们的思维很难发散，学习能力也很难提升。数学学习的过程不应是被动接受的过程，而应该是一个主动体验、探索、实践的过程，只有这样才能让学生“真学”“会学”。

基于以上分析，在其他班的教学中，笔者决定对教学过程进行一些调整，鼓励学生思考方法的多样性，以此发散学生思维，化被动为主动。

三、第二次教学流程

1. 复习旧知，引入新课

同上，略。

2. 设置游戏，引导探究

（1）第一关：火眼金睛

师：观察图1和图2，说一说它们有什么相同点，有什么不同点。

生1：相同点为都有2个三角形；不同点为图1中的2个三角形是独立的、分开的，而图2中的2个三角形是连在一起的。

师：还有其他不同点吗？

生2：小棒数量不同：图1有6根，图2有5根。

师：为什么会少1根呢？

生3：图2中的2个三角形是连在一起的，它们有一条共用的边。

由此，与第一次设计相同，学生通过观察、分析实现了预期目标，发现了“公共边”的秘密。

（2）第二关：我摆你填

学生活动1：仿照图2的摆法，同桌合作摆出10个三角形，要求每摆出1个三角形做一次记录，并将实验记录汇总形成统计表。

学生活动2：结合统计表说一说你的发现。

学生由此发现：每多摆1个三角形，需要增加2根小棒。在此环节，以小组活动为主，学生通过实验、观察、交流等活动逐渐发现图形中的规律。此环节与第一次教学设计相同，从教学反馈来看，学生参与课堂的积极性较高，气氛活跃。

（3）第三关：智慧比拼

师：这一关是通关的关键，大家一定要小心。

师：首先请大家完成一个抢答题，按照图2的摆法，我说三角形的个数，你们说需要的小棒数量。

师：你们准备好了吗？

学生齐声答：准备好了。

师：很好，请问摆出2个三角形需要几根小棒？

生4：5根。

师：5个呢？

生5：11根。

……

师：大家太厉害了，你们是怎么知道的呢？

生6：刚刚实验的时候统计过。

师：哦！原来如此。如果是20个三角形呢？（学生不语）

师：其实第二关的统计表中存在着一个大秘密，你们想不想知道是什么秘密呢？（学生探究的积极性迅速被激发）

师：谁来说一说，用算式如何表示摆出2个三角形需要5根小棒？

生7：3+2=5。

师：很好。如果摆出3个三角形需要7根小棒，用算式如何表示呢？

生8：3+2+2=7。

师：4个呢？

生9：3+2+2+2=9。

师：观察以上几个算式，是否有更简便的方法呢？（教师预留时间让学生交流）

生10：我知道了，对于3+2=5可以写成3+2×1=5，对于3+2+2=7可以写成3+2×2=7，以此类推。

师：说得很好，对于3+2×1，其中“3”表示什么？“2”表示什么？“1”表示什么？

生11：“3”表示先摆的那个三角形，“2”表示每增加1个三角形就要多摆2根小棒，“1”表示增加了1个三角形。（学生边说，教师边画，得到图4）

师：要是摆10个呢？摆100个呢？摆n个呢？

生12：3+2（n-1）。

师：很好，你们有没有不同的想法呢？

生13：刚刚的过程我也理解了，不过我在计算时是这样列算式的，对于摆2个三角形需要5根小棒，我的算式是1+2×2。

师：有没有和生13想法一致的同学？（三分之一的学生举手表示与生13的想法一致）

师：那你说一说，这里面的“1”表示什么？“2×2”又表示什么呢？

生13：“1”表示先摆1条边，“2×2”中前一个“2”表示每摆1个三角形要添加2根小棒，后一个“2”表示摆了2个三角形，“2×2”就表示摆2个三角形需要再添加“2×2”根小棒。（学生边说，教师边画，得到图5）