精心设计 关注发展

作者简介：赵远（1977—），本科学历，小学高级教师，从事小学数学教学工作。

[摘  要] 提问是教师提升学生注意力、激发学生思维活力的常用手段。教师在教学中借助一些具有启发性的、创新性的、针对性的问题可以有效点燃学生的思维火花，激发学生的无限潜能，让学生在问题的探究过程中找到思维的落脚点和知识的生长点，从而在掌握知识的基础上学会数学的研究方法，真正地学会学习。

[关键词] 提问;思维活力;研究方法

在小学数学课堂上，大多数教师会设计一些数学问题来提升学生的注意力，激发学生的思维活力，让学生在问题的驱动下学会独立思考和合作交流，进而提升课堂有效性。不过教师在提问时一定要掌握好“度”、控制好“量”，结合班级的实际学情进行量身定制，因为问题过难容易造成“冷场”，问题过于简单则无法激发学生探究的热情;问得过多容易造成思维疲劳，问得过少则很难提升学生参与的积极性。同时，为了使教学更有效，教师在问题的设计上应具有一定的针对性、方向性和创新性，只有精心的预设、灵活的调整才能使数学提问更有效。

随着新课改的不断深入，学生在教学中的地位凸显。为了能够更好地体现学生的主体地位，教师常常借助一些问题引导学生去发现、去探究、去总结，从而在理解和掌握知识的基础上学会学习，成就好的课堂。不过，若想成就好的课堂需要教师提出好的问题，只有好的问题才能让学生的思维兴奋起来，从而点燃课堂，让学生更好地融入课堂，真正成为课堂的主人，真正爱上课堂。

那么什么样的问题才是好问题呢？笔者认为，好问题应该具有一定的挑战性、创新性，只有这样才能抓住人心。当然教师在问题的设计上应注意一定的关联性，要调整好问题的梯度，只有这样才能吸引学生积极参与教学。此外，教师在设计问题时要避免为了问题而引入问题，那样会因问题缺失针对性和方向性，很难让学生获取有价值的信息，不利于学生的发展。下面，笔者结合一些具体案例，谈谈自己对数学提问策略的一些粗浅认识，以期共鉴！

一、数学提问应具有针对性

数学教学中有时会出现这样的情况：教师结合学生的实际学情设计了许多问题，学生也顺利地一一作答了。但是当学生利用新知解决问题时，却依然感觉束手无策。究其原因是教师在提问时忽略了问题的针对性，明明可以一个问题或一句话直接点明的，而教师为了营造活跃的气氛而将问题进行拆分，这样就造成了啰唆和累赘，学生难以抓住本节课的重点和核心，使得课堂出现了“伪活跃”，课堂教学效率低下。若要改变这一现状，教师要对问题进行细心打磨，使提问精练而明确，便于学生抓住问题的本质和核心，以此提升课堂效率。

案例1  认识前后

师：动物园的小动物们今天要举行运动会，你们想不想去看一下？

生（齐声答）：想。

播放小动物准备参加400米跑步比赛的视频，视频里正在介绍运动员。

师：现在请小朋友们来介绍一下参加此项比赛的各个运动员吧。（教师按下暂停键，让学生观看画面并回答问题）

生1：它们分别是小鹿、乌龟、兔子、羊驼、蜗牛。

师：很好，你们猜一猜，谁跑得最快呢？（通过“猜一猜”吸引学生的注意力）

有的学生说小鹿最快，有的学生说羊驼跑得快，有的学生说应该是兔子更快，还有的学生认为因为在龟兔赛跑时乌龟取胜了，所以应该乌龟跑得快。这样在和谐的对话交流中，学生的思维更加活跃。

师：大家想不想知道结果呢？

生（齐声答）：想。

继续播放视频，直到各选手陆续到达终点。

师：现在说一说谁是第一？谁是第二？

生2：小鹿第一，兔子第二。

师：很好！大家看一看羊驼跑了第几名呢？

生（齐声答）：第三。

师：那羊驼的前面有谁？后面又有谁呢？

生3：羊驼的前面是小鹿和兔子，后面是乌龟和蜗牛。

师：很好，那么谁在乌龟的前面，谁在兔子的后面呢？（问题提出后，学生积极回答）

师：兔子是在前面还是在后面呢？

生4：兔子在小鹿的后面，在其他小动物的前面。

师：很好！如果让你设计一个问题你会吗？

这样通过师问生答让学生掌握了提问的方法后，教师鼓励学生自己提出问题，然后通过互问互答引导学生自主地学会用“前后”来描述相对的位置关系。

教学中学生积极参与竞猜“谁跑得快”，并在回答问题的基础上提出问题，教师借助问题有效地活跃了课堂气氛。从教学反馈上来看，该问题的设计是科学的、合理的，其既从学生的已有经验出发，帮助学生认识了“前后”，又通过层次性问题的推进激发了学生思考与探索，让学生明确了位置的相对性。

以上问题的设计都是教师经过仔细推敲和打磨的，如果只是问“羊驼的前面有谁？后面又有谁呢？”虽然能够让学生理解“前后”，但是不利于学生更好地理解前后的相对性。同时，一年级的学生思维方式比较单一，在提问时如果没有前面问题的铺垫就直接问“小兔子在前面还是在后面”，学生很难像教学中那样准确地表述小兔子的位置关系。可见，教师在提出问题时既要有针对性，又要兼顾层次性，这样才能让学生更好地参与到课堂提问中来，以便于学生的思维在由易到难的逐层深入中螺旋上升。

二、数学提问应更加方向性

数学知识是抽象的、复杂的，在教学时教师如果“照本宣科”地将内容讲授给学生，学生表面上听得懂，但是在解题时往往不能灵活应用。因为直接讲授容易造成学生缺失知识生成过程，这样学生难以将新知真的学会，在知识迁移时受阻就是情理之中了。为了更好地引导学生思考，教师有必要设计一些具有方向性的问题，让学生在问题的引导下经历知识生成和发展的过程，让学生更好地理解和掌握新知;同时，让学生学会自主探究的方法，以此提升学生的学习能力。

案例2  长方体和正方体的认识

师：我们已经认识了长方体，知晓了长方体各个部分的名称：面、棱、顶点。为了更好地认识长方体，你认为接下来我们需要学习哪些内容呢？

生1：学习会涉及运算，所以应该知道各部分的数量。

师：说得很好，那你们能提出哪些关于面、棱和顶点的数学问题呢？

生2：长方体有几条棱？有几个面？几个顶点？

师：很好，现在请大家“数一数”，说一说各部分的数量。

学生仔细观察课前准备的长方体模型，通过数一数知晓了长方体各部分的数量。

师：仔细观察长方体，思考一下，除了研究以上数量，你认为还可以研究一下哪些内容呢？

生3：可以研究一下面与面的大小和棱与棱的长短。

师：很好！那你们能够根据生3的思路提出几个相关的数学问题吗？

生4：长方体的6个面之间有什么关系呢？

生5：长方体有长短相等的棱吗？

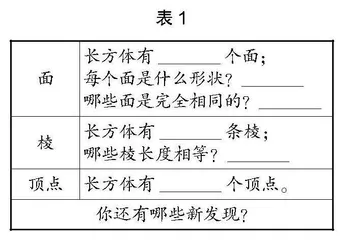
师：大家说得都非常好，接下来请大家仔细观察长方体，并通过“数一数”“量一量”“比一比”后完成表1。

教学中教师引导学生根据自己的已有经验提出问题，有目的性地培养学生的问题意识。当基本问题已经呈现后，教师将学生所关心的和必须掌握的内容进行整理，以表格的方式加以呈现，使得问题更加清晰，使学生的思考更有方向，有助于学生新知的掌握。

在执教过程中，教师以学生的已有认知为出发点，让学生通过对点、线、面的再认识更好地理解长方体的特点。在教学过程中教师并没有通过“背书”的方式让学生理解点、线、面的数量，而是让学生通过“数一数”独立完成，这样的亲身经历便于学生记忆。同时，在教学过程中，教师有目的性地引导学生提出问题，这样学生不仅会很快找到研究方向，而且有效培养了学生的问题意识，提升了学生的参与度，活跃了课堂气氛。最后，教师将问题整理归纳成了表格，清晰地呈现了长方体的基本特征，便于学生完成知识的内化。

三、数学提问应具有创新性

在数学教学中，教师在教学设计上应具有一定的创新性，让数学课堂更具吸引力和创造性。教材虽然是教学之本，但是因地区差异、班级差异等情况的存在，教材中的一些情境可能并不适合本班的具体学情。因此，教师可以结合具体情况对教材中的情境进行一些改造，通过再创造使之更适合学生的发展。那么教师创新性地使用教材时，要思考如何设计一些创新性的问题来激发学生思维的活力。

案例3  分段计费

在课前教师让学生通过与父母交流或网上查阅资料的方式，了解一些关于出租车收费标准的内容（至少查阅两个城市）。这样学生在学习新知前对分段计费有了大概的了解，进而为“分段计费”教学带来便利。

师：课前大家都进行了预习，你们对出租车的计费标准理解了吗？

生（齐声答）：理解。

师：很好！小明一家周日打算到距离家6.3千米的游乐园游玩，周末游乐园的停车位都比较紧张，所以小明一家人决定乘坐出租车前往。已知该市出租车的起步价为7元（3千米以内），超过3千米后每千米的收费为1.5元（不足1千米按照1千米计算），你能帮小明算一算，他们往返需要支付多少车费吗？

对于小学高年级的学生来讲，他们具备一定的分析能力和解决问题的能力。该问题与生活息息相关，所以该问题学生可以轻松求解。部分学生认为该问题过于简单，并未激起他们的探究热情。

基于学生的课堂表现，教师提出了一个新问题：“大家都热心地帮助小明解决了问题，现在请大家思考一下，出租车为什么要设置起步价呢？”

学生在学习数学时，尤其在解决一些生活中的实际问题时，多是从“运算”的角度去思考。因此，面对这一问题时学生感觉无从入手，课堂出现了一种停滞的状态，该问题把学生难住了。

师：你们认为设置“起步价”对谁更有利呢？司机还是乘客？

问题给出后，教师鼓励学生进行沟通、交流，大多学生认为设置起步价对司机有利，但也有少部分学生认为对乘客有利。

师：看来靠“说”是难以说服彼此了，我们需要用“算”来证明这一切。大家想一想如何用数据证明这一切呢？（教室一下子安静了下来，不一会学生已经有了答案，教师让学生进行板演）

生1：如果只坐2千米，按照每千米1.5元计算，只需要支付3元，而实际支付了7元，这样司机就多赚了4元，所以对司机有利。

生2：如果按照每千米1.5元计算，坐3千米只要4.5元;起步价是7元，这样司机可以多赚2.5元，所以对司机有利。

生3：如果坐6.3千米，按照每公里1.5元计算需要支付7×1.5=10.5元，实际支付4×1.5+7=13元，这样司机多赚了2.5元，可见对司机有利。

学生有理有据的证明，让站在“对乘客有利”一方的同学心服口服，他们自发地鼓掌赞同。

师：观察以上司机所赚的钱数，你有什么发现？（生沉思）

生4：只要超过3千米，司机就多赚2.5元。

师：那么这2.5元实际上是从哪里来的呢？

生5：其实就是起步价中的差额，如生2的计算结果。

至此，通过教师的不断追问，学生彻底理解了其中的奥秘。

师：课前我让大家收集了不同城市的收费标准，你们有什么发现吗？

生6：不同的城市收费的标准不同，有的城市是7元，有的城市是10元，有的城市是11元。

师：大家观察得真仔细，那么你们知道这个是为什么吗？

生7：大城市的人挣得多。（生笑）

师：也许有这方面的因素。客观上讲，城市越大，出行的距离就越远，所以在制定收费标准时会综合考虑这些客观因素。（生点头表示赞成）

师：结合上面计算的数据，谈谈你的感想。

生8：短距离尽量少坐出租车，这样少吃亏。

生9：司机师傅多赚点也是对的，因为送好客人后有可能就是空车返回的，这样也是需要成本的。（众生点头）

师：大家都说得很好。你们既会算经济账，又懂得体谅他人。在生活中我们尽量绿色出行，这样既省钱又环保。

这样一节普普通通的“分段计费”问题，在创新性问题的指引下学生呈现出了别样的风采。在数学教学中，教师要勇于打破常规，避免简单的“照本宣科”，善于抓住学生的兴奋点，这样才能让学生真正参与到探究的过程中，以此活跃课堂气氛，提高教学的有效性。

总之，教师要精心预设和打磨提出的问题，利用追问、反问、设问等形式来激活学生的思维，打造高效的数学课堂。