优化作业设计 提高学习效率

[摘  要] 作业是课堂教学的延续，是教学内容的综合，是知识转化为技能的保障，对学生巩固知识、形成技能、发展能力和培养思维都具有重要的作用。文章结合学生的具体情况，对作业形式进行优化，通过多变性、开放性、趣味性、层次性的作业设计，来尝试提高学生的学习效率。

[关键词] 作业设计;多变性;开放性;趣味性;层次性

作业是课堂教学的延续，是教学内容的综合，是知识的应用，是教师了解学生学习状态的窗口，对学生巩固知识、形成技能、发展能力和培养思维都具有重要的作用，因此教师需要有正确的价值观，通过有效地作业设计，成就更加高效的数学学习。那么，我们该如何优化作业设计，才能真正促进学生的可持续发展呢？笔者将结合教学实践，在文章中对新课程环境下的优化作业设计谈谈自身的一点见解。

一、多变——由单一到变式，发散思维

变式，归根结底就是创新，目的是调动学生的积极性，使其主动热情地完成作业，最终达到真正掌握知识点和题型解决方法的目的。因此，精心选择题型，运用多变式作业设计，变换条件或问题去创造新题，由单一的数学问题到变化的多题，将问题步步深化，这一系列操作可以有效解除思维定式给学生带来的束缚，发散他们的思维，提升他们的解题灵活性。当然，这里的多变性问题并非随意或盲目变题，需要以问题的本质为核心，具有明确的目的，遵循学生的认知现状。只有达成以上要求的新题，才能激发学生的解题动力，充分发挥多变性作业的效果，培养学生主动思考、善于联想和敢于怀疑的品质，最重要的是发散他们的思维和培养他们的自主探究能力。

案例1  三角形的面积

习题：已知一个平行四边形的面积为24平方厘米，则与之等底等高的三角形的面积是___________。

变题1：已知一个平行四边形的面积为24平方厘米，从中能剪出的一个最大的三角形的面积是___________。（请以虚线画出剪法，并说一说共有多少种剪法）

变题2：剪完后，平行四边形剩余部分的面积是___________。

设计意图：在以上案例中，教师可以以课本为源，以学生为本，以同质异形的变式作业引发学生的深度思考。由于变式问题兼具创新和固本两大特性，能有效地调动学生的思维兴趣进行高效解题。故而，作业设计要善变、常新，才能挖掘习题的教育功能。此外，教师应提供多变性的作业供学生思考、分析和探究，才能帮助学生巩固相关知识，实现真正意义上的“减负增质”。

二、开放——由封闭到开放，创新思维

课本习题往往都是封闭的，大多数展示其静态的形式，答案也是“非此即彼”，很大程度上制约了学生创造性思维的发展，易使学生变成答题和考试的“机器”。当前所被推行的素质教学，其宗旨便是提高学生的创新意识。因此，教师的作业也需与时俱进，由封闭到开放，使其具有一定的开放性，赋予学生广阔的思维空间，追求创新思维的发展。

案例2  四边形的分类

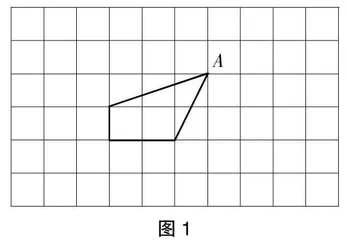
作业：完成以下“点子图”（如图1）：

（1）若往下移动点A，是否能使原图形变成梯形？若可以，点A应移到何处？

（2）若继续往左移动点A，该图形还是梯形吗？

（3）若仍然继续向左移动点A，是否能出现平行四边形？

设计意图：教师的作业设计以学生所需为出发点，以学生的思考、探究和质疑为主体，让学生积极参与到作业的完成中去，真正发挥其自身的思维潜能。以上案例中，笔者设计一个“移动的点A”，让问题变得开放、变得动态，使得学生在观察中思考，在思考中感悟，在感悟中习得。原图形的形状因问题的不同而不同，学生通过这种动态变化获得对知识、技能、方法和思想层面上的认识。这样的开放性作业不仅有利于学生加深对知识的理解，还能优化学生的思维品质，培养其勇于探索的精神，使其形成乐于探究的态度。

三、趣味——由枯燥到有趣，活化思维

数学知识大多抽象枯燥，这也是很多学生不喜数学的根本原因。在设计作业时，教师倘若能融入生动、鲜活和新颖的元素，则可以在一定程度上激发学生的思考兴趣，使其以最佳学习状态参与到教学中。因此，教师可以从具体的教学内容出发，设计趣味性作业，将枯燥的内容变得有趣，活化学生的思维，发展学生的数学智慧。

案例3  以“四边形的分类”的课堂练习为例

师：大家猜一猜老师手中是什么四边形？（教师自信封取出一张四边形图纸，并露出其中的一个锐角）

生1：平行四边形。

生2：梯形。

……

师：现在揭露谜底——这是一个不规则的四边形！大家再来猜一猜，这里又是什么四边形呢？（教师又自信封取出一张四边形图纸，并露出其中的一个直角）

生3：长方形。

生4：正方形。

……

师：这是一个直角梯形。这个信封中呢？（再一次拿出一张露出一个钝角的四边形图纸）

生5：平行四边形。

生6：不规则四边形。

师：是平行四边形。大家看，这里有一个四边形，但被剪成了一个直角三角形和一个等高的直角梯形，大家猜一猜，它原本是什么样的四边形？

……

设计意图：以上案例中，笔者以“猜一猜信封里是什么图形”这一游戏来吸引学生的注意，让学生在层层递进的“猜想”中不断思考，自觉回忆并巩固和提炼各种四边形的特征，从而深化对知识的理解。尤其是练习的最后一个环节，笔者将拼图游戏放在各种图形中综合思考，让学生通过回忆和想象，经历图形重组的过程，形成更加深刻的感悟，从而为后续图形面积的学习奠定良好的基础。

四、层次——由全体到自选，因材施练

每个学生都有不同的学习能力，不同的学生理解能力也存在着差异，在学习自然数学时自然也会表现出不同的学习效果。新课程理念要求教师关注并尊重学生的个体差异，因材施教，提高教学的针对性。面对这一要求，“一刀切”的练习显然是不合时宜的，容易出现“学优生吃不饱，学困生吃不了”的情形。因此，教师在设计作业时需关注到每个学生的实际情况，让作业内容变得有层次和弹性，争取让每个学生都能在作业中获得不同程度的体悟，得到解题的成就感。

案例4  乘法分配律

基础题：

简便计算以下各题：

（1）34×28+28×66;

（2）125×（80+8）。

说明：基础题中的题型均为基本形式：第（1）题，如先将“34个28”和“66个28”合并，则只需要直接算出“100个28”的结果即可;第（2）题，这是字母公式的活用，即将a×b+a×c=a×（b+c）这一公式反过来使用即可。

进阶题;

简便计算以下各题：

（1）25×44;

（2）99×101-99;

（3）134×34+134×25+134×49。

说明：进阶题相较于基础题，难度有了提升，相当于基础题的变式。其中第（1）题需要想到的是合理分拆数;第（2）题需要补充题目为符合乘法分配律的形式，再进行简便运算;第（3）题则是运用乘法分配律。

提高题：

计算以下各题（能简便计算的请简便计算）：

（1）（13×36+12×36）×4;

（2）53×64+37×53。

说明：提高题对于大部分学生来说要求较高，其解题思路环环相扣，需要学生具有较强的思维能力和灵活运用知识的能力。以上两道习题均需要完成两次简便运算，第（1）题应先括号内乘法分配，并使用乘法结合律再进行第二次简便运算;第（2）题需先运用乘法分配律得出“101×53”初步结果，再将数分拆，进行第二次简便运算。

设计意图：作业设计考究的是教师结合学生思维对新知识的解析。以上案例中，笔者根据教学内容的特征，设计层次性、梯度性的作业，给予学生自主选择练习的机会，基本上兼顾了每种不同状态的学生。通过这样的练习，学生对本节课所学知识的巩固与掌握状况会更好，不同状态的学生也基本都能体验到解题的成就感，进而提升学习积极性。

五、结语

总之，优化作业设计是提高课堂教学实效性的有效策略，是决胜考试的关键所在，是学生能力得以稳步提升的重要一环。教师应从学生能力的发展入手，设计具有多变性、开放性、趣味性和层次性的作业，为学生提供探究的时间和空间，从而实现可持续发展。当然，作业设计是一个需要不断探索和实践的事，唯有准确把握学生的实际情况，不断总结、不断反思，才能设计出诱发学生学习兴趣，符合学生认知发展规律的新题，达到提高学生学习效率的目的。