数学教学中基于最近发展区的障碍教学法实践

[摘  要] 障碍教学法是以“障碍”为基础的教学方法，可以激起学生思维的涟漪，触发学生去探求突破障碍的方式方法，达到下一个发展区自然生成。文章通过阐述基于最近发展区的障碍教学法的执行和实施过程，探讨这一教学法的可行性和实效性，以构建良好的教学模式。

[关键词] 障碍教学法;最近发展区;小学数学

维果茨基推崇“最近发展区理论”，要求教学着眼于学生的“最近发展区”，这样才能激起探究欲望，让学生有效超越最近发展区，从而优化教学效果。因此，教学时应明确学生的现有发展区，并在此基础上有意识地制造矛盾，设计适切的“障碍”，让学习变得富有挑战性，从而激起学生思维的涟漪，触发学生去探求突破障碍的方式方法，达到下一个发展区自然生成。基于这样的认识，本文结合多个课例，阐述基于最近发展区的障碍教学法是如何得以执行并实现的。

一、悬念障碍，引发探究兴趣

悬念就是指教师从小学生好奇心强等特征出发，创造一种科学的或进行一种创新的学习，引起学生产生各种疑问，使探究活动一触即发。悬念障碍的核心就是引发学生的探究兴趣，诱导学生创造性地思考。因此，教学中可以从学生的最近发展区出发，拟出创意性问题来设计“悬念障碍”，诱发其探究兴趣，使其主动投入揭开谜底的教学活动中。

案例1  3的倍数特征

师：同学们，今天给你们一个机会来考一考老师，看你们是不是能难倒老师。

师：你们任说一个数，我可以立刻判断它是否为3的倍数。（学生跃跃欲试，各个绞尽脑汁地抛出数字，而且有的数字大到只能使用计算器进行验证，教师都能准确而快速地进行判断。学生一个个都对教师既崇拜又好奇）

师：其实老师能这样准确地加以判断，完全是因为已经掌握了3的倍数特征，那么它究竟有何特征呢？你们可以先猜一猜。（就这样，火热的辩论展开了）

生1：我觉得个位上是3、6、9时，这个数就是3的倍数。

生2：我反对，13、16、19都满足你说的条件，但它们并不是3的倍数。

生3：我认为十位满足3的倍数就行。

生4：我不赞同，随便举例，260就不是啊！

生5：我觉得应该和各个数位都有关联，但是如何关联就不清楚了。

……

就这样，教师判断学生的最近发展区水平来精设悬念，将学生带入充满困惑之境，让学生产生迫切想要研究问题的冲动，这是引导学生进入下一个发展区的关键所在。

二、疑问障碍，诱发积极思维

学贵有疑，疑可以衍生心理上的困惑，只有拨动思维之弦，才能有所收获。当学生对知识产生疑问并盼望可以迅速解决时，容易产生一种心理期待，这就是“疑”。因此，教师要积极创造条件，使学生时常面临疑问，让学生体验这样的一种从质疑到释疑的升华，为问题的突破创造条件，从而顺利抵达下一个发展区水平。

案例2  认识厘米

师：大家看，老师手里有一根毛线，你能利用你手中的直尺量出它的长度吗？你觉得应该怎么量？（此问题的抛出，为学生提供了广阔的探讨空间，学生自然而然地进入了讨论的氛围中）

生1：这个很简单啊，当然从尺子的顶端开始量啊！

师：是吗？这样量正确吗？你们试着量一量呢？（学生一边操作一边交流，很快发现生1度量方法上的错误）

生2：尺的顶端是没有刻度的，那前面一点的长度是无法计入的，肯定是量不出准确长度的。

师：那如何才能量出准确长度呢？

生3：应该从刻度0开始量。

师：非常好，那就请你们量一量各自手中物品的长度。（学生开始着手测量，并很快有了答案，并掌握了量法）

师：大家看，老师手上的这把尺子断了，刻度0已经没有了，该如何量呢？（学生的思维浪花又一次被拨动，新的学习需求再次产生）

生4：我从刻度4开始量起，这根毛线可以量到刻度10，一共6厘米。

生5：我是从刻度6开始量起的，这根毛线量到了刻度12，也是6厘米。

师：看来，在没有起始刻度时，我们可以从任意一个刻度开始……

可见，学习过程并非简单的模仿或被动的记忆，需要学生自身在行为与心理上产生积极的、能动的内在需求。本例中，教师连续抛出问题，激发学生持久的兴趣和不竭的探究动力，让学生走入思维的大观园，使其有疑、有思、有论、有辩，通过已有的知识经验去构想、去创造，以获得测量的方法，体验测量带给人的创造性的快乐。

三、任务障碍，驱动主动探究

新课程理念倡导以生为本，以任务为载体，以培养学生数学素养为宗旨，让学生轻松愉悦地融入学习互动中。因此，教师可以结合小学生的特点，基于其最近发展区设计出一些驱动式的任务障碍，驱动学生主动探究。

案例3  长方形的面积计算

师：我们一起来求以下几个长方形的面积，并说一说你是如何求出的。

生1：可以将这个边长是1厘米的小正方形纸片铺在长方形上，直至摆满，用了几个小正方形就是几平方厘米。

师：如此短时间内就给出解决策略，真是爱动脑筋的学生，那就让我们试一试吧！（学生跃跃欲试，进行操作，很快完成了第一个长方形面积的计算，进而继续探索下一个长方形的面积计算）

生2：小正方形不够用了。（很快，学生发现这一方法的弊端）

生3：测量这个长是5厘米，宽是4厘米的长方形，12个边长是1厘米的小正方形不够铺。

师：那该怎么办呢？有没有其他办法呢？大家再想一想。

生4：我觉得可以先将这12个铺满，并做好标记，再移动这些小正方形，将其铺到未铺的位置，直至铺满。

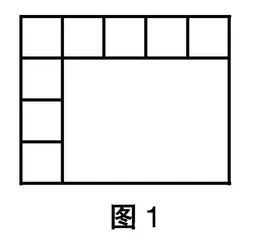
生5：我认为只需要8个小正方形就能完成。如图1，这个大长方形每一排要摆5个小正方形，刚好摆了4排，因此一共需要20个，得出面积为20平方厘米。

师：你们真是善于思考的学生。那还可以用更少的小正方形吗？（这一任务的抛出给学生的数学思考又增添了些许活力）

生6：这一次我用了6个小正方形，5个用于量长，1个用于量宽。（图2）

生7：我用得更少，只用了5个小正方形，4个量宽，1个量长。（图3）

生8：我的方法应该是用得最少的。只要1个小正方形就能完成，先用它去量长，需要量5次，再用它去量宽，需要量4次，所以可以完成任务。（图4）

师：哇，真是太厉害了，掌声是不是应该响起来……（掌声如雷贯耳，显然，生8的奇思妙想得到了大家的一致认可）

以上案例中，对学生学习思维的开启当属比较成功。教学中，教师抛出学习任务，引发学生从已有经验出发用摆小正方形的操作形式，通过摆的过程，学生知道面积计算的“源”，并学会了“思”。进一步地，教师加大任务的难度，激励学生不断思考，实现“更少的小正方形”到“一个小正方形”的突破。此任务障碍法是让学生创新思维的开启建立在最近发展区的水平上，通过一个又一个任务的驱动，迫使学生创造性地解决问题。这样的过程，明显可以感觉到学生思维的突破和学习能力的提升，这样的动力自然可以激励他们拾级而上，突破下一个发展区水平。

总之，一种教学法的应用需要经历反反复复的实践与思考，在实践中前行，在反思中完善。笔者以障碍教学法为载体，基于学生的最近发展区进行了一个阶段的教学尝试，惊喜地发现学生的求知欲和挑战欲逐步生成，思维也有了很好的发展。笔者认为这种教学法是有益的，进而提出来与广大读者分享。

作者简介：姜宁玲（1998—），本科学历，中小学二级教师，从事小学数学教育教学工作。