融合整体化思想与局部分析法的教学研究

[摘  要] 文章基于体积专题教学的实践与反思，提出融合整体化思想与局部分析法突破教学难点的改进方案，促进学生对研究对象获取全貌性的认识，感知问题的操作性过程，整体把握体积难点问题的本质。

[关键词] 整体化思想;局部分析法;体积;教学;难点

在五年级体积专题的解题教学中，笔者发现学生对于“排水法”求体积的整体化思想停留在表层性认知且对问题的操作性过程的感知不足，不能真正地把握体积难点问题的本质。因此为了让学生克服体积难点问题的认知障碍，笔者提出了融合整体化思想与局部分析法进行突破的教学改进方案。

[⇩] 一、教材中“排水法”求体积的整体化思想

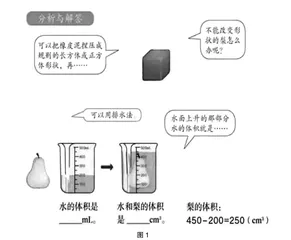
所谓体积即物体所占空间的大小，“排水法”求物体体积问题是人教版数学五年级下册第三章“长方体与正方体的体积”课题内容。该课题由图1的对话情境引入，通过图意我们可以得到以下问题：现有一个烧杯，其中装有足够的水，问如何求梨的体积？[1]

教材介绍了“排水法”求体积，由图1将梨放进烧杯中使其完全浸没，可读出烧杯中水和梨总体的体积为450cm3，而烧杯中原有水的体积为200mL，于是梨的体积为450-200=250cm3，即图1中水面上升那部分的体积就是梨的体积250cm3。

可见，教材以实验探究的形式比较放进梨之前后烧杯中水和梨总体的体积变化，使得学生能够直观地感受“排水法”求体积。“排水法”求物体体积不仅揭示了体积概念的本质——物体所占空间的大小，还给学生提供了整体化思想。

[⇩] 二、教学实践及反思

笔者在该专题的教学实践中进行了测试，其中有一道考题如下：一个长方体容器，底面是一个边长为60厘米的正方形。容器里直立着一个高1米，底面边长都是15厘米的长方体铁块，这时容器里的水深0.5米（如图2）。现在把铁块轻轻地向上提起24厘米（如图3），那么露出水面的铁块上水渍的长度是多少厘米？[2]

测试结果显示，大部分学生的解答错误，其中一部分学生不假思索地回答露出水面的铁块上水渍的长度就是24厘米;另一部分学生经过认真思考进行计算，仍陷入认识误区，出现了以下错解：

铁块向上提起24厘米后，提起部分占有的空间V=15×15×24=5400cm3，伴随着水面下降，水面下降高度为5400÷（60×60）=1.5cm，则露出水面的铁块上水渍的长度为24+1.5=25.5cm.

针对学生出现的典型错误进行分析与反思，笔者认为学生对于教材中的“排水法”求物体体积的整体化思想停留在表层性认知，且对于“铁块向上提起24厘米”问题的内在操作性过程更是感知不足。因此，笔者进行了“加强整体化思想的剖析，融合局部分析法”的教学改进探索。

[⇩] 三、融合整体化思想与局部分析法突破体积专题的难点问题

教材中“排水法”求物体体积揭示了体积概念的本质，且提供了一种整体化思想，但在培养学生的数学思维上并不全面[3]。为了让学生加深对“排水法”求体积的整体化思想及其内在操作性过程的认识，笔者设计了以下3个环节的教学方案。

1. 改编教材例题巩固整体化思想

笔者在教材例题的基础上增补以下例题：

如图4，底面积为50平方厘米的圆柱体容器中装有水，水面上漂浮着一块棱长为5厘米的正方体木块，木块浮在水面以上的高度是2厘米。若将木块从容器中取出，水面将下降多少厘米？

这个问题的难点在于，如图5，不知道原来容器中水的高度（h1），亦不知取出木块后水的高度（h2），不能简单机械地套用“排水法”。

“排水法”求体积实际上利用的是整体化思想。在此将“未取出木块时水面以下部分”作为一个整体，其中包含水的体积和水下部分的木块的体积。注意到水的总量没有变化，即水的体积不变，于是取出木块后，水面下降部分的体积应该等于原来水下部分的木块的体积。从而将问题转化为求水下部分的木块的体积，即水面下降而消失的部分的体积等于原来水下部分的木块的体积，那么问题也就迎刃而解了。具体的思考过程如下：

V水+V水下部分的木块=V水+V水面下降而消失的部分，则V水面下降而消失的部分=V水下部分的木块=5×5×（5-2）=75cm3，水面下降的高度h=V水面下降而消失的部分÷S圆柱底面=75÷50=1.5cm。

在整体化思想的指导下除了使用算术法外，还可以通过设未知数求解水面下降的高度。即设水面下降的高度为h厘米，通过分析可得到以下等量关系：50h=5×5×（5-2），50h=75，h=1.5。故可得水面下降的高度为1.5厘米。

2. 融合局部分析法加强问题探究

以上我们可以知道整体化思想有助于学生基于整体认识进行问题的解决，但是这仍是不够的，还需要学生学会全貌性地感知问题，探究问题的操作性过程，整体把握问题的本质。

笔者在整体化思想的基础上，运用局部分析法指导学生对问题进行重新解读，为方便说明，现将图4简化为正视图（如图6），具体教学方案如下：

将木块取出后，设水面高度将下降h厘米，木块周围A部分的水将填补原来木块B部分的空间，B部分木块的高度为（5-2-h）厘米，如图6所示。A部分的空间=B部分的空间，注意到A部分水的形状是一个中空的圆柱体，其体积为50h-（5×5）×h立方厘米，故可建立如下等量关系：50h-（5×5）×h=（5×5）×（5-2-h），25h=25×（3-h），h=3-h，2h=3，h=1.5。故取出木块后，水面下降的高度为1.5厘米。

局部分析法反映了问题的操作性过程，即取出木块后原来A部分的水填补在B部分的空间。局部分析法相较于整体化思想，不仅知悉问题总体的原来结构和结果状态，还能经过剖析，感知问题的局部操作性过程。

3. 融合整体化思想与局部分析法突破难点问题

整体化思想就是将问题的若干对象当作一个“整体”，充分协调问题中部分与整体的关系，使部分的功能服从于整体的要求，从而达到解决问题的目的[4]。局部分析法是选取问题中合适的局部为研究对象，根据问题的情境，对研究对象的操作性过程进行分析的方法。融合整体化思想与局部分析方法，对于辩证突破体积难点问题有重要的意义。整体与局部两者结合，可对问题进行全貌性分析，使得学生全貌性地认识问题，感知问题的操作性过程，整体把握数学问题的本质。下面运用该思想方法解读文前的测试题：

铁块向上提起24厘米后，从整体化思想的角度来看，铁块在水中的空间总共消失了15×15×24=5400cm3。再从局部分析法的角度来看，如图8所示，原来铁块周围A部分的水填补了阴影部分B的空间（铁块消失的空间），即A部分的空间等于B部分的空间。注意到铁块未完全提离水面，还有一部分铁块留在水中占用了一部分空间，考虑到A部分水为中空的水柱，即其底面为有中空的正方形，面积为60×60-15×15=3375cm2。具体的解答步骤如下：

铁块轻轻向上提起24厘米后，其原来占有的空间为15×15×24=5400cm3，伴随着水面下降，水面下降的高度为5400÷（60×60-15×15）=1.6cm，则露出水面的铁块上水渍部分的长度为24+1.6=25.6cm。答：露出水面的铁块上水渍部分的长度为25.6cm。

因此，融合整体化思想与局部分析法突破体积难点问题的教学，一方面可以让学生整体感知问题，另一方面可以让学生通过局部的分析感知问题中的操作性过程。两者相融合，学生就能够全貌性地认识问题，探究问题的操作性过程，以此牢牢地把握问题的本质。

[⇩] 四、思考与启示

通过融合整体化思想与局部分析法突破体积难点问题的教学研究，笔者得到以下启示：

（1）教师不能仅仅停留在教材原始素材的基础上照本宣科，应成为教材的开发者。教师通过对教材的深入剖析，挖掘教学内容蕴含的思想方法，并选取多种角度对问题研究的对象进行分析，可使学生能够在同化的基础上顺应拓展性问题解决难点。

（2）在教学内容和思想方法上进行深入挖掘，应立足学生的思维最近发展区[5]，重视直观化教学，重视操作性探究过程。在引导学生突破难点问题的过程中，教师应以学生已有的认知基础作为落脚点，着眼于学生的认知水平，把握研究对象的本质及其内在的联系，引导学生多层次、多视角探究问题，加深学生对问题的操作性探究过程的认知[6]。

参考文献：

[1]  人民教育出版社课程教材研究所小学数学课程教材研究开发中心.义务教育教科书（数学五年级下册）[M]. 北京：人民教育出版社，2020.

[2]  蒋顺，李济元. 小学奥数举一反三：五年级[M]. 西安：陕西人民教育出版社，2017.

[3]  李婷，卢建川. 运用整体把握与分离组合思想探究“烙饼问题”[J].中小学课堂教学研究，2018（02）：22-25.

[4]  武良文，孙秀梅. “整体思想”在数学解题中的运用[J]. 数学学习与研究，2004（12）：6-7.

[5]  李祎. 另眼看难点[J]. 数学通报，2016，55（07）：1-3+10.

[6]  郑煜芬，卢建川. 溶液混合问题“反比关系”的分析与教学研究[J]. 数学教学通讯，2021（07）：3-5+24.