关于概念教学的三点建议

[摘  要] 针对当前“放任式”“灌输式”“牵引式”概念教学的现状，文章提出概念教学的实施建议，认为概念教学应凸显概念形成过程，尊重学生个体差异，关注本质感悟，进而使学生在探究、质疑、发现和归纳中触及概念本质，完成对概念的建构。

[关键词] 概念;建构;建议;小学数学

概念教学是小学数学教学的重要组成部分。“放任式”概念教学令学生浅尝辄止，“灌输式”概念教学让学生一知半解，“牵引式”概念教学令学生将信将疑，这些倾向都影响着学生对概念的深度理解，进而影响学生对数学知识的掌握。基于这种现状，笔者提出了关于概念教学的三点建议，期望对广大教育同仁有所借鉴和思考。

[⇩] 一、概念教学应凸显概念形成过程，切勿追求“速成”

概念教学中，教师要注重学生的逐层体验，循序思考，让学生逐渐触摸到概念的本质，不能追求“速成”，也不要追求一步到位，要按照从表象到抽象、从感性到理性、从理解到运用的思路逐步展开，使学生渐渐地触及概念的本质，进而体验到数学概念形成和发展的逻辑线索[1]。

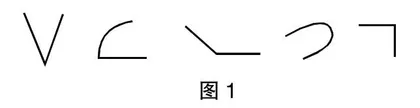
比如讲到“角的认识”时，教师将教学过程分为以下几步：第一步，观察生活中的角。在这一步中，教师先引入生活中常见的物体，如三角板、课本、钟表等，使学生在这些物体上找到角，然后顺其自然地引入数学中的角。第二步，建立角的表象。在此步中，教师先利用多媒体逐个隐去原来的图形，抽象出数学中的角，然后在黑板上画出一个角，并使学生理解数学中把尖尖的点叫作角的顶点，两条直直的边叫作角的边，从而得出“角有一个顶点和两条边”的结论。第三步，画角。在此步中，教师引导学生画出一个角——先画一个点，从这个点出发画一条直线，再从这个点出发向另一个方向画一条直线，这个图形就是角。第四步，辨角。教师出示几个图形（如图1），使学生自主判断哪些图形是角，哪些图形不是角，并说明原因。在这个过程中，学生对角的概念的认识逐步稳固。第五步，找角。教师出示图形（如图2），引导学生找一找、说一说图形中各有几个角。在这个过程中，学生对角的概念的认识进一步加深。第六步：制角。在此步中，教师引导学生用身边的材料制作一个角。有的学生把两根小棒摆在一起，制成一个角;有的学生把一张圆形纸进行折叠，制成一个角;有的学生用两根吸管制成一个角;有的学生用两根硬纸条制成一个角。于是教师引导学生得出：尽管做角用到的材料各不相同，做出的角的形状、大小也不一样，但是它们都有一个顶点、两条边。从而再次凸显出角的本质属性。第七步，比角。在此步中，教师引导学生进行数学操作，使学生认识到：角的大小与边的长短无关;角的开口越大，角就越大，角的开口越小，角就越小。

“磨刀不误砍柴工”，概念教学犹如熬煮一锅好粥，需要经过一系列工序，既要精心选择配料，又要掌握好火候。教学中，教师为了使学生逐步建立起对角的概念的认知，设计了丰富的数学活动，把概念教学过程分为层次鲜明、逐层递进的7个步骤，各个步骤循序渐进，由表及里、由浅入深，既符合概念教学的基本规律，也与小学生的认知规律高度契合。正是这种“温火慢炖”式的教学使得学生真正感受到数学概念产生的过程，从而促进学生对概念的深度理解。

[⇩] 二、概念教学要尊重个体差异，切勿“一刀切”

新课标指出，数学教学面向全体，实现人人学有价值的数学。小学生由于成长背景、认知经验和思维水平的差异，在面临同一数学现象时会产生不同的数学理解[2]。在概念教学过程中，教师要尊重学生的个体差异，要为学生各抒己见提供一定的时间和空间，在学生畅所欲言的基础上寻找机会，引发学生思维碰撞，使学生逐渐建立起对概念的深度理解。

比如讲到“长方形的面积”时，教师引导学生采取平铺法推导长方形面积公式。

师：请同学们利用1平方厘米的小正方形铺一铺，看看这个长方形的面积是多少。

（学生操作，教师巡回指导）

生1：我用面积是1平方厘米的小正方形去铺，每行有4个，一共有3行，所以这个长方形的面积是4×3=12（平方厘米）。

师：对。也就是说求小正方形的总数可以用每行的正方形个数乘行数。那么这个长方形的长是多少，宽是多少呢？说一说你是怎么知道的。

生1：这个长方形的长是4厘米，宽是3厘米。因为沿着长边铺一行是4个小正方形，所以长是4厘米，沿着宽铺一列是3个，所以宽是3厘米。

师：长方形的长与什么有关？宽与什么有关？

生1：长方形的长与每行的小正方形个数相等，宽与小正方形的行数相等。

师：据此，你怎样推导出长方形面积公式？

生1：长方形面积=小正方形总数=每行个数×行数=长×宽，所以长方形面积=长×宽。

师：同学们都是这样平铺的吗？

生2：我们小组只铺了一行一列，因为一行有4个小正方形，每列有3个小正方形，所以我们据此推断小正方形的个数是4×3=12，长方形的面积是12平方厘米，我们依然根据“每行个数与长”“行数与宽”之间的关系，推导出长方形的面积=长×宽。

生3：我们小组并未用小正方形平铺的办法，而是直接用尺子来测量。通过测量我们发现，长方形的长是4厘米，所以1行能摆放4个小正方形，长方形的宽是3厘米，所以一共能摆放3行，这样我们就得出一共可以摆放4×3=12（个）小正方形，所以长方形的面积为12平方厘米，推导出长方形的面积=长×宽。

师：同学们更喜欢哪种方法呢？

生4：“半铺法”比较省时省力。

生5：“测量法”最简便，但是不容易想到。

学生的个体差异决定了他们的思考力、操作力都不相同。从“满铺法”到“半铺法”再到“测量法”，体现了学生思维层次的差异性。在教学过程中，教师充分尊重学生的这种差异性，引导学生采取不同的办法推导出长方形的面积公式，在此基础上，教师引导学生对这三种方法进行对比，从而在辨析中引发学生思维碰撞，由此，在因材施教的基础上完成对概念的完整建构，真正实现“不同的人在数学上得到不同的发展”。

[⇩] 三、概念教学要关注本质感悟，切勿“浅显化”

“为教之道在于导，为学之道在于悟。”数学概念具有抽象性，小学生学习数学概念往往离不开现实事物的支撑，但是教师的教和学生的学不能仅仅止步于具体的情境和实物，还要从具体事物中剥离、抽象出概念的本质。因此，在概念教学中，教师要重点引导学生摆脱于具体的情境和实物，将思维的焦点集中于对概念本质的理解和感悟[3]。

比如讲到“认识”时，教师引导学生用图形表示出。有的学生把长方形平均分成2份，取出其中1份涂上颜色表示;有的学生把等腰梯形或圆形平均分成2份，取出其中1份涂上颜色表示。教师问道：“为什么同学们画的图形不一样，涂色部分大小也不一样，却都能表示呢？”学生讨论后得出结论：不管什么图形，只要平均分成2份，取出其中1份，就可以用表示。在此基础上，教师引导学生用完全相同的一个正方形表示，有的学生把这个正方形“横着”对折成2份，取出其中1份涂上颜色表示;有的学生把这个正方形“竖着”或“斜着”对折成2份，取出其中1份涂上颜色表示。教师问道：“为什么对折的方式不同，却都能表示呢？”学生讨论后得出：不管怎样对折，只要平均分成2份，取出其中1份，就可以用表示。

“百般说教不如帮人悟道”，教学中，教师通过引导学生操作和思考，使学生摆脱具体实物（长方形、等腰梯形、圆形）和具体对折方法（“横着”对折、“竖着”对折、“斜着”对折）的束缚，从中抽象出的本质：平均分成2份，表示其中的1份。这就有效避免了学生对分数概念认知的情境化和浅显化，使学生的认知直达概念本质。

“欲速则不达”，要让学生更好地掌握数学概念，概念教学就不应片面地追求“速成”，而应该使学生经历探索、感悟过程，使概念教学的过程更加“精致”，这就需要教师要有“磨刀不误砍柴工”的觉悟和“打破砂锅问到底”的执着，让学生在探究、质疑、发现和归纳中触及概念本质，完成对概念的建构。

参考文献：

[1]  宋运明. 核心素养导向的小学数学概念教学——融合优秀教师课例的探析[J]. 基础教育课程，2020（20）：41-45.

[2]  马志浩. 深度建构数学概念的实践与研究——以小学数学中高段概念教学课为例[J]. 中国教师，2020（10）：105-106.

[3]  章婷. 聚焦核心素养  促进概念建构——小学数学概念教学有效性策略探寻[J]. 小学教学研究，2020（21）：47-49.