中考数学“代数推理类”试题的分析与思考

[摘  要] 《义务教育数学课程标准（2022年版）》在“数与代数”学习领域增加了代数推理的明确要求. 研究者依据新课标对重庆市近5年中考数学A卷从内容维度、过程维度、水平维度进行分析，从中得到教学质量提升的启示：代数推理应该注重代数推理形式、注重论证过程、注重证实说理，为一线教育教学提供参考.

[关键词] 代数推理;中考数学;代数推理能力

作者简介：王玉琴（1999—），重庆师范大学在读硕士研究生，从事数学教育研究.

通信作者：童莉（1976—），博士，教授，硕士生导师，从事数学教育测评、数学教师专业发展研究.

前言

推理能力是高素质人才的基本要求，培养推理能力是新一轮课程改革的重要内容. 在国际数学教育领域，推理能力被认为是学生数学素养评价的核心指标之一. 国际学生评估项目（Program for International Student Assessment，PISA）2022中，数学素养框架的核心是“数学推理”，将其融入问题解决过程. 在真实情境中，数学表述、应用、诠释都围绕数学推理来展开[1]. 新加坡教育部将推理作为数学问题解决的一个重要过程[2]. 澳大利亚 F-10数学课程关键思想将推理作为关键词[3];美国国家教育进展评估（National Assessment of Educational Progress，NAEP）旨在从内容领域和数学复杂性这两大维度（测评要素）评价学生的数学能力，数学复杂性高水平要求学生在问题解决过程中能够进行完整推理证明[4];《英国国家课程（数学）》中为不同年龄阶段的学生设立有关推理的教学目标[5]. 在中国，数学教育纲要文件中都强调了数学推理在教学中的重要性. 尤其是《义务教育数学课程标准（2022年版）》（下称“新课标”）中将推理能力作为数学思维的主要表现之一[6]，推理按照领域可分为几何推理、代数推理和统计推理，新课标在一贯重视几何推理的基础上，特别强调代数推理，并开发了培养学生代数推理能力的课程内容实例.

中考是初中学业水平考试的简称，传统的数学教学往往认为中考主要考查的是几何推理和代数计算，因而重视学生几何推理能力的培养，忽视学生代数推理能力的培养. 根据教育部意见[7]，中考从2019年起取消考试大纲，省级统一命题将严格依据《义务教育课程标准》，代数推理能力必将成为考查的重点，而中考具有强烈的导向作用，从中考试题中分析代数推理能力的考查情况，能够洞悉未来代数推理的趋势和发展动向，探求学生思维发展的趋势，为一线数学教学提供参考，因此，本文以近五年重庆市中考数学试题为分析对象，探讨代数推理能力的考核要求，对培养学生的代数推理能力做出思考.

中考数学代数推理试题的分析

框架

对中考数学试题的分析往往是分维度进行的，如唐亚军等人从几何知识、几何技能和几何思维水平三个方面分析了中考中的几何试题[8];陈妙莹从“3 大知识领域+5 大类型+推理形式”构成分析维度，比较 了2011-2021 年广东广西两省区中考数学中的合情推理型试题[9]. 因此，本文对中考数学代数推理试题的分析拟从内容、过程、类型三个维度来进行.

1. 内容维度

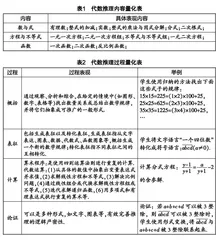
新课标中对推理能力的定义是：“推理能力主要是指从一些事实和命题出发，依据规则推出其他命题或结论的能力. ”代数推理就是运用数与式及其运算进行推理，得出结论和做出判断的过程[10]. 代数推理是以代数知识为背景的思维形式，是区别于几何推理与统计推理的思维类型，是主要围绕抽象算术、函数思维、数量关系三大代数内容的思维形式[11]. 本文将初中数学内容按数与代数进行划分，包括数与式、方程与不等式、函数. 参照人教版初中数学教材的制作，制定了对应的内容量化表（见表1）.

2. 过程维度

J.J.KAput[12]提出了代数推理的两个核心：一是对规则和约束的系统化概括，二是基于语法进行的推理和对常规符号系统表达的概括活动. 通过对代数结构、函数、关系和协同变化的研究和运用，概括、表征、计算和论证代数知识和问题解决策略之间的联系的思维过程. 因此，从过程角度分析，代数推理过程包括观察、推测、表征、一般化、证明、验证等要素，推理形式包括溯因推理、归纳推理、演绎推理等. 本文将代数推理思维分为四个过程：

概括：鲍建生曾指出代数的本质是发现处理问题的一般模式. 在本研究中沿用BlAnton对一般化给出的定义：在观察、分析后给出的情景中找出数量关系或归纳概括出数学规律，并抽象成可推广的一般形式.

表征：用数学方式准确地将“一般化”后得到的数学规律表示出来也是代数推理中十分重要的一部分. 表征包括：生成表征和转化表征. 生成表征是生成一个新的表征或将新的表征添加到现有的表征方式中. 转化表征是指用某种表征方式解释另一种表征方式中的数量关系.

计算：学生能够准确、有效地按算术程序和代数法则进行计算和检验. 算术程序是使用四则运算法则进行重复的计算，而代数程序包括但不限于：①从具体的数值中抽象出变量表达式并求值;②求解线性方程和不等式;③通过线性组合或代换求解线性方程组或不等式;④迭代求解递归函数;⑤用多项式和有理式执行重复的算术等. 这里要区分代数推理与代数运算，代数推理是指通过代数式的推导、变形和运算来解决数学问题的方法. 它基于代数的基本运算规律和逻辑推理，通过数学符号和代数表达式的变换来得到问题的解答，是基于法则，运用条件，指向问题解决的综合思维活动.

论证：学生能为推理的结果做出有说服力的解释，证明结论的正确性. 能以适当的方法来证明自己通过归纳、概括得到的数学结论是合理的，是可以推广到一般的情形中的. 论证可以是文字说明，也可以借助图形或表格加以解释. 在测试卷中通常以代数证明的形式出现.

以新课标中例66的第（2）问（如图1）为例，对解题过程进行举例分析. 具体表现过程见表2.

3. 类型维度

推理主要分为类比推理、归纳推理、演绎推理[13]. 何勇将代数推理题分为：代数运算型、结构转化型、代数说理型三种[14]. 叶旭山将代数推理分为三个类型[15]：证实类推理、推测（演）类推理、应用类推理，其中推测（演）类推理又分为运算推理、归纳推理、类比推理;应用类推理分为封闭模型推理和开放模型推理. 谢春艳将代数推理分为分析性推理、创造性推理和实践性推理[16].

综合已有研究中对代数推理试题的分类，本文对代数推理题进行了如下分类（见表3）.

重构推理型：图2是2022年重庆市中考数学A卷第11题，本题利用一元一次不等式组以及分式方程，在解与解集以及特定条件的限制下，要求推理出所有满足条件的a的值之和，题目主要对不等式以及分式方程的结构进行转换，得到满足所有限制条件的特定的数，本题属于“重构推理型”.

证实说理型：图3是2023年重庆市中考数学A卷第10题，本题通过逻辑推理的方法，证明三个相关结论的正确性，本题属于“证实说理型”.

代数建模型：图4是2024年重庆市中考数学A卷第22题，本题以生产生活为情境，要求学生建立相应的一元一次方程和分式方程的模型，并在此基础上推理得到需要的结果，本题属于“代数建模型”.

综合以上分析，本文将从以下三个维度对重庆市中考数学试题中的代数推理类题目进行分析：①过程：概括、表征、计算和论证;②内容：数与式、方程与不等式、函数;③类型：重构推理型、证实说理型、代数建模型，形成了如图5所示的中考数学代数推理试题分析框架.

中考数学代数推理试题分析

结果

1. 选取试题

本文以重庆市近五年中考数学A卷为研究样本，对重庆市中考数学中代数推理的考查情况进行调查. 研究旨在了解重庆市中考数学对代数及代数推理的考查现状，并为提高初中生的代数推理能力提供建议.

2. 内容维度分析

参照内容量化表，对重庆市2020年到2024年中考数学A卷的代数内容进行统计）. （见表4）

根据本文对重庆市近五年中考数学试题中的代数推理题的分析，不难发现中考数学试题中代数推理题的对应分值在试卷总分中的占比为20%～30%，平均占25.87%. 在考查年份中，2022年的代数部分考查占比最高，达到30.67%;而2024年代数部分考查占比最低，仅有21.33%，其代数推理更多地隐含在整个试卷的其他部分进行考查. 在代数的三大板块的考查中，数与式占31.96%，方程与不等式占42.27%，函数占25.77%. 可以看出，代数推理考查中方程与不等式考查较多，函数部分考查较少.

3. 过程维度分析

解决代数推理问题主要分为概括、表征、计算、论证四个过程，对2020年至2024年中考试题代数推理部分进行分析（见表5），得到平均占比为：概括占83.07%，表征占93.54%，计算占100.00%，论证占62.21%.

非常值得注意的一个数据是，计算过程占到代数推理题的100%，也就是每道代数推理题中都含有计算过程. 计算过程是指解决数学问题时需要进行计算的过程，当然这里的计算包括代数计算以及数值计算.

表征过程是指将问题转化为代数式、图表、函数图象等形式的过程，这一过程的占比也非常高，其平均占比为93.54%，甚至在2020年和2021年考查的每一道代数推理题都涉及表征过程，可见代数推理题涉及表征的生成或者转化.

论证过程是指解决问题时进行推理逻辑的完善，而在四个过程中，论证过程占比很低，平均只有62.21%，甚至在2020年其占比只有57.14%. 在当前中考数学中，代数证明并不是主要的考查方向，但论证过程对于代数推理的重要性不可忽视，因此，后续可能需要加强这方面的考查.

综上所述，代数问题的解决过程包括概括、表征、计算、论证四个部分，每个部分都是不可或缺的. 学生在备考过程中，需要熟练掌握每个过程的技巧，全面提升代数推理能力.

4. 类型维度分析

对2020年至2024年的代数推理试题进行分析（见表6），可以得出占比最多的是重构推理型，其平均占比为41.59%. 这种类型的题目要求考生根据已有的条件和规律，在一定的限制下，通过转换和重构式子的结构和形式，得出所需的结论. 这就要求考生具备较强的逻辑思维能力和操作能力，能够灵活运用已有的知识和技能进行推理和变形.

证实说理型试题相对于其他类型的代数推理试题而言，平均占比最少，仅有21.24%. 证实说理型是一种要求考生使用逻辑推理和论证方法，根据已知的结论和相关证据进行分析和说明，以证明该结论的正确性或得出特定结论的试题类型. 这种类型的试题在类比几何推理中可以类比证明推理题，因为它们都要求考生通过逻辑思考、严谨推理来得出结论，提高了考生的学术思维和证明能力. 然而，在现有的中考推理中，证实说理型的试题比重较小，相比之下，重构推理型的试题占比更多. 这一现象导致代数推理试题中证明型推理的形式较为弱化，也使得考生对于代数推理的逻辑性和重要性的认识不够充分.

代数建模型试题的平均占比为37.16%，这种类型的试题要求考生通过分析实际情境，从中识别相关数量之间的关系和重要特征，并利用符号和变量建立数学模型，将现实问题抽象成数学问题. 在此基础上，考生需要应用推理、运算等数学方法，对建立的数学模型进行分析和求解.

5. 交叉分析

从代数推理试题的类型分布分析中可以发现，重构推理型试题对于数和式子的考查占比最高，达到了21.13%（见表7）. 以2024年A卷第18题为例，考生需要巧妙利用题目中的已知条件，运用等式的性质以及数的不同表达形式之间的相互转换，最终获得在所有限制条件下的正确结果. 重构推理型试题的考查范围广泛，要求考生具备深厚的数学功底和较强的逻辑推理能力. 这一类型的试题旨在培养考生的问题解决能力和数学思维能力，要求考生能够利用已有的知识和技巧，在一定的限制条件下，对问题进行重构和转换，进而得出正确的结论.