基于问题解决的初中数学单元教学设计研究

[摘  要] 单元教学设计是从一章或者一单元角度出发，将一个单元的知识看成一个整体，培养学生整体思考问题的能力，让学生更加全面、系统地理解数学知识，提升学生数学综合能力. 单元教学设计是一个全新的、富有生命力的命题，它为数学教学提供了新思路. 教师要加大对相关理论的研究，打破常规教材体系的束缚，以发展学生为目标，精心创设问题情境，引导学生亲历知识生成和生长的过程，培养和提升学生自主学习数学的能力.

[关键词] 单元教学设计;整体;数学能力

作者简介：杜星兰（1987—），本科学历，中学一级教师，从事初中数学教学与研究工作，曾获重庆市初中数学青年教师优质课大赛一等奖.

在新课程改革的推动下，单元教学愈发受到关注，学界倡导教师要从整体把握数学课程，进行单元教学设计. 从教材安排上来看，因受学生认知水平、课堂教学时间等诸多因素的影响，许多相似或相关的内容会被安排到下个主题或下册教材中，使得数学知识的链式结构出现“断裂”，这样势必会影响学生建构知识体系，阻碍知识迁移能力的提升. 当然，在新知教学中，教师会采用多样的教学手段和教学策略引导学生对已有相关知识进行复习回顾，但是在此过程中因为缺少学生主动建构的过程，使得新旧知识之间可能难以形成有效关联，影响整体教学效果. 基于这一现象，在实际教学中，教师应认真研究整个学段的教学内容，实现对数学教学的整体把握及整体安排，凸显知识点之间的横纵联系，以此使学生对知识的掌握更加系统，为知识的灵活应用打下坚实的基础. 以下笔者将平行四边形和特殊平行四边形的内容进行整合和重构，逐步优化个体知识结构，提高学生自主学习数学的能力.

总体分析

1. 教材内容分析

在学习本单元内容前，学生已经学习了全等三角形，掌握了平行线的性质，对平行四边形和特殊平行四边形有一定的认识，这些知识内容为本课内容的学习提供了前提. 通过教学本单元，引导学生将平行四边形转化为特殊平行四边形，渗透转化的数学思想方法，为后续多边形的研究奠定基础.

2. 学情分析

小学阶段虽然学过平行四边形和长方形、菱形等特殊平行四边形，但是没有规范的定义，只是感性认识. 另外，初中生的几何基础相对较弱，为了激发学生的学习兴趣，构建高效、生动、有趣的几何课堂，教师从学生已有知识经验出发，通过实验操作、直观演示，设疑诱导等多种教学手段进行启发和指导，以此培养学生的直观想象素养，提高学生的动手实践能力，发展学生的数学素养.

3. 教学方式分析

随着新课程改革的不断推进，学生的主体价值凸显，教学中教师应贯彻“以生为主体、以师为主导”的教学理念，按照学生的认知规律精心创设问题情境，引导学生思考，逐步提高学生的自主学习能力. 根据本课内容的特点，教师应以观察发现法为主，直观演示法为辅，让学生通过教与学的有效互动推导归纳得出结论，逐步提高学生的逻辑推理能力.

教学过程

1. 复习引入

问题1：对于平行四边形大家都不陌生，你能说说它的定义吗？

追问1：如果让你画一个平行四边形，你会画吗？

追问2：如何说明所画四边形是平行四边形呢？

师生活动：学生动手画平行四边形，教师巡视指导.

教师利用几何画板进行演示，引导学生通过操作、归纳得出平行四边形的文字定义. 几何画板的演示是从特殊到一般的数学思维过程，有利于培养学生的逻辑推理能力.

在此基础上，教师引导学生利用几何语言表达平行四边形的判定，如：因为两组对边分别平行，所以四边形是平行四边形.

设计意图  引导学生复习平行四边形的定义及性质，可以让学生进一步熟悉平行四边形的一般性研究策略，为接下来研究特殊平行四边形做好铺垫.

2. 探索新知

问题2：周知，平行四边形具有不稳定性，若将其进行拖拉，则平行四边形的形状会发生变化，变化后的图形还是平行四边形吗？变化过程中，是边发生了变化还是角发生了变化呢？

问题3：随着角度的变化，是否会出现一些特殊情况？其他角可以换成90°吗？

师生活动：教师预留时间让学生动手做，用脑想，并利用几何画板进行演示，将平行四边形转化为矩形.

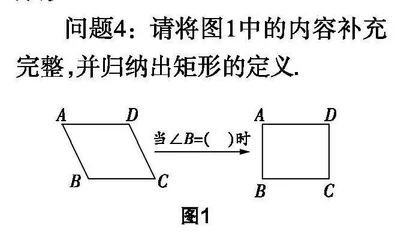
问题4：请将图1中的内容补充完整，并归纳出矩形的定义.

师生活动：学生动手操作，感受平行四边形的不稳定性，教师引导学生观察边和角的变化. 教师利用几何画板演示平行四边形转化为矩形的过程，并提出问题，引导学生思考角度变化与特殊平行四边形的关系. 教师鼓励学生归纳总结，并用数学符号语言表征.

问题5：结合以上内容说一说，矩形和平行四边形有何共同点？矩形是平行四边形吗？它有何特殊之处呢？

师生活动：学生讨论并回答问题，教师引导并总结. 教师利用几何画板展示平行四边形与矩形的关系，强调矩形是特殊的平行四边形. 学生尝试归纳矩形的定义，教师巡视指导. 学生展示归纳结果，教师点评并补充完善.

设计意图  通过动手操作和动画演示，直观呈现平行四边形和矩形之间的区别与联系，渗透转化思想.

紧接着，教师利用几何画板展示图2、图3两种情形，从而让学生得到菱形和正方形的定义及性质，同时通过变化让学生体会菱形与平行四边形，正方形与平行四边形、矩形、菱形等不同图形间的区别与联系，促进知识的深化.

设计意图  在此过程中，教师以平行四边形为基础，通过增加条件将平行四边形分别转化为矩形、菱形、正方形，让学生切实体会图形之间的变化规律，这样图形的定义、性质等就变得一目了然，不仅方便学生理解和记忆，而且可以帮助学生建构完善的知识体系，从而为灵活应用打下坚实的基础. 同时，在此过程中，教师引导学生利用不同的数学语言归纳相关定义，旨在培养学生的数学语言表达能力，提升学生的直观想象素养. 另外，让学生经历实验、演示、综合、归纳等活动，有利于进一步强化学生的逻辑推理能力，培养其思维的深刻性、严谨性.

3. 运用新知

例1  判断下列命题是否正确：

（1）在四边形ABCD中，若其中一个角为直角，则该四边形为矩形;

（2）在平行四边形ABCD中，若其中一组对边相等，则该平行四边形是菱形;

（3）在平行四边形ABCD中，若∠A=90°，则该平行四边形是菱形;

（4）在平行四边形ABCD中，若其中一个角是直角，且一组邻边相等，则该平行四边形是正方形.

师生活动：教师先让学生独立思考，然后组织学生进行小组讨论，分享彼此的思考，分析具体原因，使学生在互动交流中加深对相关定义的理解，培养学生的思辨能力.

例2  如图4，在△ABC中，已知AD是∠BAC的角平分线，过点D分别作AB，AC的平行线，使其交AB于点E，交AC于点F，求证：四边形AEDF是菱形.

师生活动：教师引导学生理解题目. 由于该题难度不大，教师预留时间让学生独立证明. 证明过程如下：因为DE∥AC，DF∥AB，所以四边形AEDF为平行四边形. 又AD平分∠BAC，所以∠BAD=∠CAD. 又DE∥AC，所以∠ADE=∠CAD. 于是有∠BAD=∠ADE，所以AE=DE. 由此根据菱形的定义，问题得以解决.

例3  如图5，在Rt△ABC中，∠A=90°，点D是BC上一点，分别作DE∥AC，DF∥AB，使其分别交AB和AC于点E和点F，求证：四边形AEDF是矩形.

师生活动：教师提出问题后，鼓励学生积极思考，并上台展示其解题过程. 学生利用矩形的定义顺利地证明了结论.

设计意图  运用是加深知识理解，培养学生数学应用能力的必经之路. 教学中，教师要从学生现有认知水平出发，精心创设有效的问题，让每个学生都能参与其中，以此通过问题的解决加深学生对相关知识的理解，增强学生的学习信心.

4. 归纳总结

问题6：本节课主要学习了哪些内容？谈谈你有哪些收获，还存在哪些问题？

师生活动：教师引导学生以小组为单位进行归纳总结，并引导学生利用集合的形式表示几种特殊平行四边形之间的从属关系.

设计意图  教师提供时间让学生进行课堂小结，逐渐完善个体知识结构，培养学生的归纳概括能力.

教学思考

新课标强调学生核心素养的培养以及课程内容的整体性、结构化整合，于是单元整体教学应运而生. 本课教学中，教师对教材内容进行重组和加工 ，从学生已经理解并掌握的平行四边形入手，通过添加条件自然引出特殊平行四边形，让学生学会用整体的眼光看问题，逐步完善个体知识结构，为后续多边形相关知识的研究打下坚实的基础.

对于平行四边形和特殊平行四边形的相关内容，学生在小学阶段就接触过，而且这些图形在生活中也比较常见，为此本单元的相关内容是学生易于理解和接受的. 在本课教学中，若教师直接将相关定义和性质告知学生，学生也是可以理解和接受的，但由于自主探究过程的缺失，使得学生难以形成深刻的记忆，不利于学生可持续学习能力的提升. 因此，教师没有采用告知式的教学方式，而是创造机会让学生去发现、去探索、去归纳，这样一方面可以加深学生对相关知识点的理解，另一方面也可以培养学生多角度地阐述自己观点的能力，有利于提升学生的综合能力和综合素养.

总之，在初中数学教学中，教师要勇于打破教材系统的束缚，注重基础的培养和整体性的提高，强化知识的转化和应用，让学生更好地理解和掌握知识，提高学生的数学学习能力.