抓住问题根源 回归数学本质
作者: 冯玉德
[摘 要] 为考查学生对基础知识和基础技能中蕴含的数学本质的理解,鼓励学生思考而不是记住或复述几何中的“模型”,在命制试题时应抓住数学本质,创造性地开发和利用课程文本资源. 文章以教材中的题目为素材,通过研究这些模型中隐圆的由来与其生成的边、角关系,完成对一道试题的命制.
[关键词] 试题命制;教材;数学本质
作者简介:冯玉德(1982—),本科学历,中学一级教师,从事初中数学教学工作,福州市教育系统先进工作者,长乐区数学学科带头人.
考试是教学评价的有效途径之一,教学评价决定教学活动的实施,影响教师教学的内容、方式、侧重点,同时使学生通过客观的评价结果对学习过程进行自我评价、反思,对学生的学习活动具有导向作用. 笔者在图形与几何模块的教学实践活动中发现很多学生能够识别经典几何模型,但又囿于模型,在题目中“看不到”几何模型时会显得束手无策. 究其原因,这部分学生对几何模型的认识只停留在几何直观上,虽能够识别,但不能理解其本质. 因此,如果尝试以教材中的题目为素材,就会发现很多本质上具有相同背景的题目. 本文从人教版九年级课本题目出发,由一对直角的两边分别相交形成“A字型”“K字型”“飞镖型”相似模型都可由隐圆构造的实质,通过研究这些模型中隐圆的由来与其生成的边、角关系,完成对一道试题的命制.
笔者希望通过这道“旧词新唱”的试题唤起学生对数学本质的探索兴趣,同时说明在教师的教学研究过程中,可以深入思考课本上例题与练习题,体会不同模型间的共性,抓住数学实质,增强教学的有效性.
试题呈现
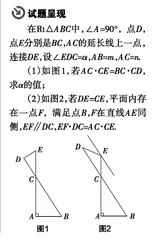
在Rt△ABC中,∠A=90°,点D,点E分别是BC,AC的延长线上一点,连接DE,设∠EDC=α,AB=m,AC=n.
(1)如图1,若AC·CE=BC·CD,求α的值;
(2)如图2,若DE=CE,平面内存在一点F,满足点B,F在直线AE同侧,EF∥DC,EF·DC=AC·CE.
①求EF的长(用含m,n的式子表示);
②连接AF,DF,求∠AFD的度数(用含α的式子表示).
命题立意
(一)知识立意
本题考查了相似三角形的判定定理、性质定理、勾股定理、90°的圆周角所对的弦是直径、等边对等角、三角形的中位线定理、直角三角形的性质、三角形的外角定理.
(二)能力立意
本题考查了学生的数感、符号意识、空间观念、几何直观、推理能力、应用意识和创新意识.要求学生能够观察等积式化归出比例式,从而想到相似三角形;题目中用字母表示数,体现符号意识;通过等腰三角形想到直角三角形,通过两边分别相交的直角得到隐圆,从而发现解题的关键.
(三)素养立意
本题考查了学生的数学抽象、逻辑推理、直观想象这三大素养. 要求学生能把第(1)小题中的数学本质抽象运用到第(2)小题中,兼用逆向思维与正向思维对结论与条件进行分析综合,结合所学知识对解题方向直观把握.
命题过程
(一)命题素材
命题以人教新版九年级下册第35页例2和第36页练习1中的基本图形(如图3,图4)作为素材. 这两题设置的意图是让学生掌握相似三角形的判定定理3,识别题目中“公共角”这一隐含条件.
(二)命题思路
1. 图形的一般化
仔细观察图3与图4,特殊的是这两个图判定相似用到的两对角,除去公共角,另一对都是直角. 再仔细观察,图4中的点E沿AC平移,直至点E和点C重合,图形就转化为图3了. 于是,笔者萌生了一些思考:保持ED⊥AB,点E继续沿AC平移会怎么样?点E沿AC反向延长线平移又会怎么样?于是有了图5、图6.
2. 发现隐圆
在点E沿直线AC平移的过程中,垂直和相似是一直存在的. 但是,这四幅图更为本质的内涵不止于此. 垂直与很多知识都有联系,但是观察这四幅图,两个直角的两条边始终分别相交,连接两个交点BE,不难发现,点D,点C始终在以BE为直径的圆上(如图7-图10),这也就是在变化中不变的本质.
到此,此类图形完成了本质的统一. 因此,命题时只选取其中一种(即图7)作为题干的基本图形.
3. 画板探索
利用几何画板画出Rt△ABC,如图11-图13. 观察点E的运动过程与隐圆圆心F的运动轨迹,发现圆心的运动轨迹是一条直线l,且l∥AC. 连接DF,FC发现∠DFC在运动的过程中角度不变.
在这个基础上,对三角形相似的因果进行置换,将相似转化为比例式,将比例式转化为等积式得到基础题干,再利用基础几何图形的性质转化等积式中的因数,形成一道完整的试题.
(三)命题方案改进
1. 第一稿
如图14,在Rt△ABC中,∠A=90°,点D,E分别是BC,AC的延长线上的点,连接DE,若AC·CE=BC·CD,求证:AB2+AE 2=DE 2+DB2.
分析 本题主要考查了相似三角形的判定定理与性质定理、勾股定理. 需要连接EB,能够体现点D和点A在以EB为直径的圆上,但是后续求证的问题与此无关,“有来龙,但无去脉”,脱离了命题的本来意图.
2. 第二稿
如图14,在Rt△ABC中,∠A=90°,点D, E分别是BC,AC的延长线上的点,连接DE,AC·CE=BC·CD,存在一点F到点D,E的距离相等,点F到点A,B的距离相等.
(1)使用尺规在图14中作出点F,连接AF,DF;
(2) 求∠AFD与∠DCE的数量关系.
分析 本题考查了尺规作图的能力、线段垂直平分线的定义、相似三角形的判定定理与性质定理、90°的圆周角所对的弦是直径,体现了笔者利用几何画板找到的规律. 但是图中存在的相似关系可以通过几何直观看出来,仍未实现“去模型化”.
3. 第三稿
在Rt△ABC中,∠A=90°,点D,E分别是BC,AC的延长线上的点,连接DE,设∠EDC=α.
(1)如图15,若AC·CE=BC·CD,求α的值;
(2)如图16,若DE=CE,平面内存在一点F,满足点B,F在直线AE同侧,EF∥DC,且EF·DC=AC·CE,连接AF,DF,求∠AFD的度数(用含α的式子表示).
分析 本题考查了相似三角形的判定定理与性质定理、勾股定理、90°的圆周角所对的弦是直径、等边对等角、三角形的中位线定理、直角三角形的性质、三角形的外角定理. 能体现图形的实质,同时需要学生思考两个小题之间的关系,从认识模型到理解模型的实质. 但是第(1)小题与第(2)小题之间的跨度太大,需要一个引导学生思维过渡的桥梁.
解答思路
这道题的第(1)小题题干出现了等积式AC·CE=BC·CD,根据等式的性质,可将其转化为比例式. 学生可以从几何直观去感受,图中存在的相似三角形为△DEC与△ABC,因此,题中的AC·CE=BC·CD应转化为=,从而证明△DEC∽△ABC,求出α的值.
在完成了第(1)小题之后,需要对该小题蕴含的图形关系进行思考,图形中存在一对两边分别相交的直角,对直角的特殊性的思考是对本题的重大突破.对直角的思考一:90°的圆周角所对的弦是直径,从这个思路出发,尝试连接EB,点D和点A在以EB为直径的圆上. 对直角的思考二:直角三角形斜边上的中线等于斜边的一半,从这个思路出发,尝试连接EB,取EB中点F,连接FD和FA,则EF=FB=FD=FA,从而E,B,D,A四点共圆.
第(2)小题的图形与第(1)小题相比,保留了对顶角相等这一条件,但是不再有“双垂直”,根据试题思维的递进性,应从变化中寻找或构造不变,即我们需要在第(2)题的△DEC中构造垂直. 利用等腰三角形构造直角三角形的常见思路有两种:一种是利用三线合一定理作底边中线,本题中可作CD边上的中线;另一种是利用直角三角形斜边上的中线等于斜边的一半,倍长一腰,本题中可延长CE至点G,使得CE=EG. 这两种方法都能完成第(2)题①.
完成第(2)题①后再来审视这个结果:EF=BC,EF∥BC,延长CE与BF相交于一点,形成一个三角形,EF是这个三角形的中位线,而CE与BF的交点恰是前面所说的利用△DEC构造垂直的第二种思路中的点G. 从这里回过头去看①,应该优选“倍长一腰”法.
到这里图形已经完全回到了第(1)小题的思考中,∠AFD实际上是一个圆心角,可利用圆周角定理求∠AFD的度数.
命题拓展
在Rt△ABC中,∠A=90°,点D,点E分别是射线CB,CA上一点,连接DE,设∠EDC=α.
(1)如图17,若AC·CE=BC·CD,求α的值;
(2)如图18,若DE=CE,平面内存在一点F,满足点B,F在直线AE同侧,EF∥DC,且EF·DC=AC·CE.
①求EF的长(用含m,n的式子表示);
②连接AF,DF,求∠AFD的度数(用含α的式子表示).
命题反思
(一)关注学生主体地位,分层考查核心素养
试题应能作为客观评价学生的一种工具,能考查学生的核心素养. 为了呈现区分度,体现命题的效度,更全面地评价学生,一份试卷里要有各种难度梯度的试题,尤其少不了“画龙点睛”的压轴综合题,笔者在本文中命制的就是一道综合题. 在命制综合题时,特别要注意各小题之间的难度递进关系与思维方法的共性,使学生在螺旋上升的思维过程中体会试题揭示的规律.
(二)围绕教材研究教学,思考课本模型实质
考试是教学评价的一种手段,对教师的教学具有导向作用. 命题遵守“源于课本而又高于课本”的原则. 在教学过程中,正需要把“源于课本”的题目理解透彻,厘清其内核,在保持内核的基础上进行变式、拔高立意. 如庖丁解牛,从“所见无非牛”到“目无全牛”;从“技”开始,更进一层达到“道”. 学生的核心素养正是在这样的过程中落地生根的.
(三)发挥信息技术作用,提升教学研究效率
以图形与几何模块的教学研究为例,几何画板作用巨大. 研究课本例题及练习题时,先思考题干条件的“定”与“动”. 利用几何画板动画演示图形的运动过程,适当添加辅助线,寻找在图形的变化过程中不变的数量关系或位置关系.