大单元背景下的跨学科融合教学的探究

[摘 要] 新课标要求教师丰富教学方式，“探索大单元教学，积极开展跨学科的主题式学习和项目式学习等综合性教学活动”.“勾股定理”一课，将数学与历史学科整合，培养学生多学科综合分析和解决问题的能力.

[关键词]大单元教学；跨学科；勾股定理

基金项目：2022年东莞市年度规划课题“大单元背景下的初中数学与历史跨学科教学的实践研究”（2022GH629）.

新时代召唤新教育，新教育需要新教学.大单元教学是课程的需要，依据《系统论》的基本原理，整体优于部分，整体决定部分，整体大于部分之和，我们需要促进系统内的各构成要素的协同与整合.大单元教学能避免“只见树木、不见森林”的零散，长期如此学生就能见到一片绿洲.

《义务教育数学课程标准（2022年版）》明确指出：学生通过数学课程的学习，适应现代生活，掌握进一步学习的必备基础知识、基本技能、基本思想和基本活动经验.如何达到上述目标？笔者做出如下解释：将数学学习与生活结合，借鉴历史经验完善自己的学习体系.

我们常说，数学来源于生活，生活即数学；我们又说，今天发生的事情将成为历史，生活即历史，那么将历史搬进数学教育是多么的合适.我们可以在数学教学过程中重演历史，站在巨人的肩上，借鉴别人的经验完善自己.课堂中教师带领学生科学地探索历史，引导学生主动体验、建构，积累数学基本活动经验，为长远学习打下基础.

跨学科融合教学的实践

现结合“勾股定理（第1课时）”新授课教学，阐释如何进行跨学科融合教学，增强学生发现问题、提出问题的意识，提升学生分析问题、解决问题的能力.

1.内容分析

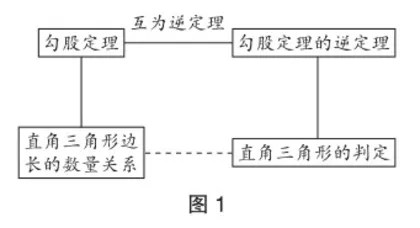
人教版教材八年级下册第十七章“勾股定理（第1课时）”是章起始课，具有统领全章的作用，思想深刻，育人价值高[1].其教材结构如图1.

本校学生在七年级上学期的数学寒假作业中，有一项任务是读一本好书——《奇妙的数学史》，并写一篇500字以上的读后感.从批阅读后感中笔者发现，一位学生对勾股定理印象比较深刻，他借此机会细细揣摩，深入探索了勾股定理这一知识点，并在读后感中写道：“我们每个人都是数学家，因为我们发现问题，并努力尝试解决问题.哪怕这个问题已经被人解答了，但没关系，因为我挑战了自己，经历了由未知到已知的过程，你应该为自己骄傲.”的确如此，对于本课时的教学，我们将采取大单元教学视野下数学融合历史跨学科教学，激发学生自主学习的欲望.

2.教学目标

（1）了解勾股定理的历史背景，掌握勾股定理；体会赵爽发现勾股定理的过程.

（2）能通过割补法构造图形证明勾股定理.

（3）经历“发现—探索—猜想—验证”等学习活动，发展学生的几何直观、逻辑推理等核心素养，让学生感受从特殊到一般、数形结合、转化与化归等思想方法.

3.教学重点、难点

重点：探索并证明勾股定理.

难点：感悟从特殊到一般、数形结合、转化与化归等思想，培养几何直观、逻辑推理等核心素养.

4.教学过程

（1）课前小测，唤醒数学思维

填空：

①在△ABC中，∠B=20°，∠C=70°，则∠A= ，△ABC是 三角形.

②如图2，每个小方格正方形的边长为1个单位，则格点三角形的面积是 .

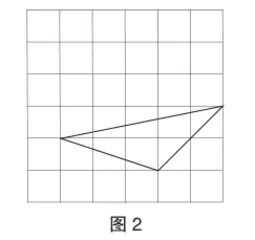
【教学分析】 课前小测的设计意图是唤醒本节课相关联的知识，利用已有的知识解决未知的问题，发展学生的知识迁移能力.学生在学习勾股定理前，已经通过测量、拼图、折纸等活动，证明了三角形内角和定理，学习了直角三角形两锐角互余的性质，学生树立的推理意识以及活动中积累的经验，都为本节课探究和证明勾股定理奠定了基础.第②小题通过“割补法”求格点三角形的面积，发展学生的类比思想，因为本节课在探究勾股定理时，需要求格点四边形的面积.

（2）剧本引入，培养数学兴趣

旁白：相传2500多年前，古希腊著名的哲学家、数学家、天文学家毕达哥拉斯有一次在朋友家做客时，发现朋友家用砖铺成的地面图案（如图3）特别有趣，陷入沉思……

穿着奇特的服装，挂上络腮胡子，扮演毕达哥拉斯的学生一出场，立刻引得全班同学哈哈大笑.“毕达哥拉斯”盯着地板，左看看右看看，兴奋地自言自语道：“好奇妙，这图案中竟含有这样特殊的数量关系，太神奇了！”

【教学分析】 毕达哥拉斯激发了学生的好奇心，学生迫不及待想知道毕达哥拉斯发现了什么.学生带着好奇心，走进历史长河，走进毕达哥拉斯的世界，历经知识的演变.

（3）任务驱动，积累活动经验

教师设计富有挑战性的学习任务，教学时给学生发放一页讲义，讲义上有四幅7×7的格点图（如图4），提出了三个任务：①利用下列网格，画出几个格点正方形；②关于画出的正方形，你发现了什么？③结合图形说说你是如何求这些正方形的面积的.

【教学分析】 这三个学习任务将学生带入学习情境.学生画出了很多个格点正方形，如图5，这些正方形分为两类：第一类正方形的边长为水平方向；第二类正方形的边长为非水平方向.

教师再用启发性的语言引导学生通过表格（如图7）中的数据，发现分割（如图5）的直角三角形的两直角边的长度与格点正方形的面积存在着规律，格点正方形的面积是边长的平方，而正方形的边长刚好是分割直角三角形的斜边.学生非常兴奋地发现一个结论：直角三角形两直角边的平方和等于斜边的平方.教师顺势向学生提出疑惑：这个结论对任意的直角三角形都成立吗？

若设直角三角形两直角边的长度分别为a和b，斜边的长度为c，会有a2+b2=c2吗？如果要说明这个结论是对的，就需要证明.请学生利用割补法试一试，证明这个结论.

【教学分析】 此教学环节渗透从特殊到一般、数形结合等数学思想，培育几何直观、逻辑推理等核心素养.在这个学习过程中，学生再次经历科学家探究之路，体验科学家发现勾股定理时的兴奋之情.教师引导学生用自己的语言表达结论，并转化为图形语言和符号语言，验证勾股定理.真理需要不断地打磨、推敲，有限数量的直角三角形得到的结论，不足以形成真理.如果结论对所有直角三角形成立，具有一般性，这样的结论才有研究价值.这样的探索过程渗透科学思想，才能合理进入验证勾股定理环节.教师的教学设计也符合定理教学的基本套路“发现—探索—猜想—验证”.笔者认为，这样的课程设计是契合深度学习理念的.

（4）历史文化，弘扬爱国情怀

勾股定理又名毕达哥拉斯定理，是欧氏几何的基础定理，由于它有着重要的应用价值而闻名于世，同时也是数学史上第一个将代数与几何两大数学脉络联系在一起的定理，被公认为是数学最美的定理之一，也是历史最悠久，最家喻户晓的定理之一，可是，为何一个数学公式能够享有这么多的美誉？那是因为勾股定理极具实用性，人们可以利用它来计算边长、确定角度、规划面积.勾股定理的发现还推动了数学两个千古难题的解决，即计算圆周率和计算曲线长度.勾股定理更是增进了人们对空间的认识，也促进了数学领域的发展.同时勾股定理是证明方法最多的定理之一.其证明方法除了我们用的割补法，还有拼图方法，比如中国古代著名的数学家赵爽，他的“勾股圆方图”注文是数学史上很有意义的文献，它详细阐述了《周髀算经》中的勾股定理，并进行了证实，即著名的赵爽弦图（播放视频）.

【教学分析】 学生会对自己本节课的探究过程相当自豪，因为他在本节课上的学习活动重演了伟大科学家的探索轨迹.他们通过认识勾股定理的历史文化背景，提高了自信心，激发了学习数学的兴趣.教师向学生讲述中国古代数学家在勾股定理方面的伟大功绩，激发学生爱国之情，培育民族自豪感，教育学生打好数学知识基础，为中华民族的伟大复兴而努力学习.

（5）建构勾股树，欣赏“分形迭代美”

教师利用几何画板，画出探究勾股定理的形成图（如图8），联想形状，命名勾股树.

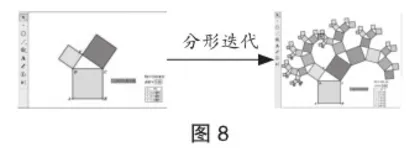
【教学分析】 学生在看到这幅美丽的图案时，表现出惊讶和兴奋的样子.他们难以想象原以为枯燥乏味的数学，能创造出如此具有美感的图形.教师以此点拨道：“身边的雪花、蜂窝都是由一个简单图形重复形成的.”数学上有一个分支专门研究这样的图形，叫分形几何.这一举措利用数学的“分形迭代美”开阔了学生的视野，激发了学生学习数学的热情，培养了学生善用数学的眼光观察世界的习惯，为未来的“数学家”们的养成打下了基础.

教学启示

《深度学习：走向核心素养》一书指出：教学的意义，在于它能够通过对人类历史实践成果的学习，使年轻人有信心、有毅力、有能力沿着人类实践的步伐向前，连接过去与未来，成为推进人类历史发展的主人[2]，这也道出了教育的价值.

1.数学与历史融合的美妙

建构主义教学理论指出，单元教学强调从单元整体出发进行教学设计，突出教学目标、内容和过程的整体性、联系性和发展性.“勾股定理（第1课时）”作为章节的起始课，对整体建构的初中数学起始课教学有着重要的意义：第一，通过介绍本章知识结构图，让学生找到学习方向；第二，走进勾股定理的历史背景，再现历史.本校学生通过阅读《奇妙数学史》，已初步了解勾股定理，如果再采用“灌输式”教学，没有教学意义，只会让学生对数学增添一分厌恶.本课例中，教师没有盲从教材，而是创造性地使用教程，把教材视为一种资源，结合历史学科，将历史剧、历史情境、历史文化等形式搬进数学课堂.在任务驱动课堂中，学生来一次真正的大体验，成为一个个科学家，重演勾股定理的发现过程，不止知其然，也能知其所以然.多元的课堂文化丰富了学生的学习体验，学生从中获得价值感和成就感，养成主动学习的能力，以期在未来的学习生涯中，遇到类似的情境，有发现问题、提出问题的意识.笔者认为，这就是有意义的教学.

2.大单元教学的育人价值

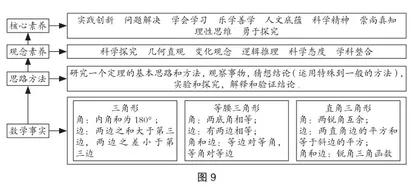
《义务教育数学课程标准（2022年版）》指出“课程目标的确定，立足学生核心素养发展，集中体现数学课程的育人价值”.基于对课程标准的分析，从数学事实、思路方法、观念素养、发展核心素养四个维度分析育人价值（图9）.

结语

史宁中教授指出：数学教育的终极培养目标是让学生“会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界”.本节课，执教者培养了学生的数学核心素养，利用真实情境，让学生经历完整的思维过程，即“发现—探索—猜想—验证”.定理教学的课堂模式是“活动—参与”，执教者认真钻研教材，将教科书中毕达哥拉斯的传说故事演绎到课堂中，使学生经历勾股定理的发生、发展过程，以便他们在未来的学习生活中养成严密审慎的思考习惯，即使面对类似的情景，也能主动思考，主动从课本中寻找答案.所以对于数学学习来说，不仅要关注学生知识的获得，更重要的是培养学生自主学习的能力，这才是我们作为教育工作者的终极目标.

参考文献：

[1] 李军，魏强.聚焦思维：数学教学的根本要义——以“勾股定理（第1课时）”教学为例[J].中学数学教学参考，2021（17）：10-13.

[2] 刘月霞，郭华.深度学习改进丛书深度学习：走向核心素养（理论普及读本）[M].北京：教育科学出版社，2018.