范希尔理论指导下的平面几何教学

[ 摘 要 ]在范希尔理论指导下，研究者以“多边形内角和定理”为例，提出应从学生现有的思维水平出发，结合教学实际设计符合学生最近发展区的教学活动，让学生在逐层的探索中逐步提高自身的几何思维能力及几何素养，切实提高学生解决平面几何问题的能力.

[ 关键词 ]范希尔几何教学理论；几何思维能力；几何素养

范希尔理论自诞生以来一直备受关注，该理论将几何教学分为五个教学阶段，即学前询问、引导定向、阐明、自由定向、整合，为设计层级递进的教学活动提供了依据.在初中平面几何教学中，大部分学生几何直观、逻辑推理等几何素养比较缺乏，使得学生整体的几何思维能力处于较低水平，影响几何教学效果.为了改变这一局面，教师应该认真研究教学、研究学生，从学生现有思维水平出发，设计符合学生已有认知的由浅入深的探究活动，以此通过逐层探究，让学生的思维能力螺旋上升.笔者在教学“多边形内角和定理”时，以范希尔逐层分析框架为指导，让学生在逐层探究中体验了数学发现的魅力，提高了学生的几何思维能力，促进了学生数学核心素养的落实.现将教学设计分享给大家，供参考.

教学目标

1.引导学生经历探索多边形内角和公式的过程，培养学生的几何思维能力.

2.通过观察、操作等活动提高学生的实践能力，让学生体会分类、转化的数学思想.

3.在分类、转化、推理等数学活动中培养学生良好的思考习惯，体会从特殊到一般的研究方法，发展学生的推理能力.

教学设计

1.学前询问

设计1 视频展示生活图片，引导学生观察生活中的多边形，如足球、扳手、房屋平面图等，让学生画出对应的多边形，然后进行展示.

大部分学生可以通过观察、分析、对比等活动正确画出对应的多边形.当然，在实际操作中，也有学生因忽视“首尾相连”这一特征而得到错误的结果.师生和生生的互动交流可以完善学生的原有认知，帮助学生深刻理解多边形的概念.

设计意图 以学生熟悉的生活情境为背景，让学生直观感知生活中的数学，激发学生的探究欲.在绘制多边形的过程中，学生会自然地与之前所有的三角形内容进行对比，通过模仿画出四边形、五边形等，并能够结合三角形的学习经验来描述四边形、五边形的特点，最终形成多边形的概念.

2.引导定向

设计2 结合三角形的学习经验，画一画、猜一猜、算一算下面图形的内角和是多少.（课件给出四边形、五边形、六边形）

学生虽然知道三角形的内角和是180°，但是并不能确定其他凸多边形的内角和度数，此时教师不要急于呈现过程和方法，而应引导学生自主分析组成要素及特征，大胆地给出自己的猜想，然后进行组内交流.

设计意图 学生根据学习长方形、正方形的经验易猜想四边形的内角和是360°，但是对于五边形、六边形却难以靠经验完成猜想.此时，教师可以引导学生观察正方形、长方形和其他四边形，分析它们的共性特征，大胆猜想，继而引出下面的数学活动.在此过程中，教师引导学生从特殊出发，让学生体验从特殊到一般的数学思想方法，提高学生的思维品质.

3.阐明

学生结合已有经验猜想四边形的内角和为360°，但是对于如何推理演绎比较模糊，在本阶段，教师要引导学生进行推理验证，体验结论的合理性.

设计3 四边形的内角和是360°吗？你会验证吗？

课前教师为学生准备了若干不同类型的四边形，鼓励学生以小组为单位，通过量一量、拼一拼等活动进行验证，并展示学生的交流成果.

设计意图 引导学生通过量、剪、拼等活动验证猜想，在此过程中，教师引导学生观察图形之间的关系，为接下来的探究活动做铺垫.

通过以上活动，学生虽然能够给自己的猜想一个合理的解释，但是由量、剪、拼等操作活动得到的结论并不严谨，需要教师引导学生进一步证明，以此让学生体验数学的严谨性，逐步培养学生的理性思维.

设计4 以小组为单位，将刚刚的若干四边形剪成若干三角形.要求：所剪三角形至少有一条边是原来四边形的边.

活动中，教师鼓励学生从不同角度思考，运用不同的方法剪拼，并让学生对以上剪拼结果进行分类，然后投影展示剪拼成果.

设计意图 通过进一步的剪拼活动，引导学生将图形分一分，逐渐将四边形与三角形建立联系，从而为接下来的转化证明提供依据.

设计5 结合以上的分一分活动，你们是否能够证明四边形的内角和为360°呢？

预留充足的时间让学生交流、讨论，寻找不同方法验证结论.活动中，学生的主体作用得以激发，促进了教学质量和学习品质的提升.教师板书学生的交流结果：

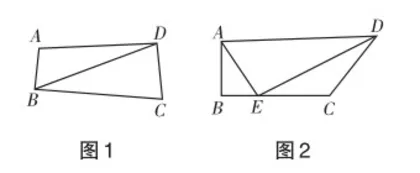
方案1 如图1，连接BD，将四边形ABCD分成两个三角形，则四边形ABCD的内角和为180°×2=360°.

方案2 如图2，在BC边上任意取一点E，连接AE，DE，将四边形ABCD分成三个三角形，此时四边形ABCD的内角和为3×180°-180°= 360°.

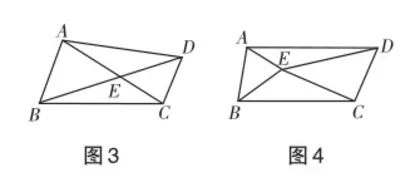
方案3 如图3，连接AC，BD，将四边形ABCD分成四个三角形，则四边形ABCD的内角和为4×180°- 360°=360°.

方案4 如图4（与方案3相同），在四边形ABCD内任取一点E，连接EA，EB，EC，ED，则四边形ABCD的内角和为4×180°-360°= 360°.

设计意图 在探究四边形内角和的过程中，教师引导学生通过剪、拼将四边形转化为三角形，以此将新知转化为旧知，最终应用三角形的知识推算出四边形的内角和.这样既丰富了学生的活动经验，又让学生体会到了转化思想方法的价值，提高了数学迁移能力.同时，在以上探究活动中，教师让学生对操作结果进行分类，并分层展示学生的探究结果，让学生学会了分类讨论思想方法，提高了学生的数学素养.

4.自由定向

接下来，教师要引导学生将推导四边形内角和的方法迁移至其他图形中，以此强化学生的原有认知，提高学生的逻辑推理能力.

设计6 思考以上分割方法，有何共同之处？哪种方法最简便呢？

设计7 你能运用最简便的方法分割五边形、六边形，并计算五边形和六边形的内角和吗？

此环节中，教师让学生独立完成，然后进行组内交流，并让各组代表呈现组内交流结果.从学生学习反馈来看，大部分学生能通过经验的成功迁移顺利解决问题.为了深化知识理解，提高学生的语言表达能力，教师让学生表述其分析和解决问题的过程.分析过程如下：图1是从四边形的顶点出发，添加一条辅助线将四边形分割成两个三角形；图2是从四边形一条边上的点出发，添加两条辅助线将四边形分割成三个三角形；图3、图4是从四边形内的一点出发，添加四条辅助线将四边形分割成四个三角形.无论从辅助线的数量还是从运算的难度来看，从顶点出发最简便.呈现学生分析结果后，教师投影展示学生的最佳分割方案，并给出验算过程：五边形的内角和为180°×3，六边形的内角和为180°×4.

设计意图 通过对比分析让学生选择最佳方案，让数学探索变得更加轻松、愉悦，提高学生的数学学习信心.

5.整合

设计8 结合以上计算方法，请总结归纳n边形的内角和.

教师引导学生以最简分割方案为依据，思考在分割过程中，添加几条对角线，形成几个三角形，由此自主发现规律.

设计意图 引导学生通过经历由特殊到一般的抽象过程，锻炼数学抽象素养，培养数学学习能力.同时通过经历以上过程，使所学知识形成一个完整的知识体系，有利于提高学生的思维品质，促进学生数学核心素养的落实.

设计9 小组自主设计相应练习，尝试应用公式解决问题.

设计意图 教师将设计练习的主动权交给学生，充分发挥学生的主体作用，调动学生参与练习的积极性.同时通过自编自答，检测学生的知识理解水平，培养思维的严谨性、灵活性和变通性.

这样通过以上5个阶段的设计，学生经历了由特殊到一般、由具体到抽象的过程，培养了学生的逻辑推理、数学抽象、直观想象等素养，学生体验到了数学探索的乐趣，增强了学习信心.