关于一次函数行程问题的解法探究

[ 摘 要 ]一次函数行程问题是对一次函数知识应用的体现，问题可分为元素对应图象型和元素共用图象型两类，探究解析时均可以采用解图“三步法”.文章开展方法解析，并结合实例强化探究，以期对师生的教学或备考有所帮助.

[ 关键词 ]一次函数；行程；方法；思路；图象

一次函数行程问题是初中数学的重点问题，问题中将一次函数与图象相结合，可全面考查学生对一次函数的性质与图象的掌握情况，以及解图能力.从函数中的元素与图象的对应情况来细分，可将问题分为两类，一类是元素对应图象型，即每个元素分别对应图象；另一类是两个元素共用一个图象.两类问题均可以采用解图“三步法”来破解.

方法、思路总结

1.思路构建

用解图“三步法”求解一次函数行程问题，顾名思义分为三步，即看、找、变，看图识条件，找图挖信息，变图构思路，具体如下.

第一步：看，看横、纵坐标分别表示的意义，题设中通常会给定条件，该步需要结合图象理解条件.

第二步：找，找图象中的关键点，包括起点、终点、转折点，同时确定每个点所代表的实际意义，理解点背后的含义.

第三步：变，探寻分析图象里的变化趋势，结合题意理解每段图象的实际意义，挖掘其中的隐含信息，如速度变化、变更方向等.

2.解法总结

求解问题时可以采用两种方法：一是使用函数的实际意义，结合追及、相遇等问题列方程或不等式解题；二是使用函数的解析式，直接利用图象的实际意义，推理分析.具体求解时也可综合两种方法，灵活变通.

分类探究问题

1.元素对应图象型探究

元素对应图象型，即问题中的元素均有各自的对应图象，通常在同一直角坐标系中，对应不同的图象，图象中含有多条直线.使用解图“三步法”求解元素对应图象型问题时，重点是对图象的解读与信息获取，需要采用数形结合的方法，提取其中的关键信息，转化为相应的条件，下面讲解示例.

例1 已知快车和慢车分别从A市和B市同时出发，匀速行驶.先相向而行，慢车到达A市后停止行驶，快车到达B市后，立即按原路原速度返回A市（调头时间忽略不计），结果快车与慢车同时到达A市.快、慢两车距B市的路程y1，y2（单位：km）与出发时间x（单位h）之间的函数图象如图1所示.

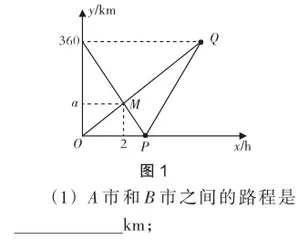
（2）求a的值，并解释图中点M的横坐标、纵坐标的实际意义；

（3）试分析快车与慢车迎面相遇以后，再经过多长时间两车相距90 km.

【图象分析】

下面针对一次函数的图象，采用解图“三步法”进行分析，具体如下.

第一步，看，确定坐标轴所表示的含义.平面直角坐标系的纵坐标表示的是两车距B市的路程，横坐标表示的是车的行驶时间.

第二步，找，明晰图中关键点的含义.图象中x=0时，两车均没有出发，则两车之间的距离就是A，B两市之间的路程.

点M：为两直线的交点，表示的是两车在出发2 h后相遇.

点P：为快车所代表的直线与x轴的交点，表示的是快车和B市之间的距离为0，表明快车到达B市.

点Q：为两车所代表直线的交点，表示两车距离B市均最远，表明两车同时到达了A市.

第三步，变，探寻图象中变化趋势的含义.根据图象的变化趋势可知：慢车和B市的距离在一直增大，说明方向不变.而快车和B市的距离先变小后增大，说明快车达到B市后立刻返回.两车最后一起到达A市，说明相同的时间，快车行驶的路程是慢车的2倍，即快车速度是慢车速度的2倍.

【过程解析】

（1）根据函数图象中数据的意义，可直接得出A，B两地之间的距离，即A市和B市之间的路程是360 km.

（2）已知快车与慢车同时出发，又同时到达A市，分析可知：在整个行进过程中，相同时间内，快车走了两个A市与B市之间的距离，而慢车只走了一个A市与B市之间的距离，所以可推知快车的速度是慢车速度的2倍.

设慢车的速度为x km/h，则快车的速度为2x km/h，根据题意可得2（x+2x）=360，可解得x=60，2×60=120，则a=120.所以点M的横坐标、纵坐标的实际意义为：两车出发2 h后，在距B市120 km处相遇.

（3）根据第（2）问可知，快车的速度为120 km/h，到达B市后又回到A市的时间为360×2÷120= 6（h）.慢车的速度为60 km/h，到达A市的时间为360÷60=6（h），如图2所示，下面结合图象分段讨论.

【解后评析】

上述为元素对应图象型一次函数行程问题，探究时采用了解图“三步法”，把握坐标轴的含义，理解其中的关键点，分析变化趋势挖掘隐含信息.求解时采用了把握图象信息，构建方程求解的策略.

2.元素共用图象型探究

元素共用图象型，即问题中的元素共用图象，通常在同一直角坐标系中，两个或两个以上的元素共用一次函数，此时纵坐标一般表示两车或两人之间的距离.对于该类问题，同样可以按照解图“三步法”来分析，需要重点关注共用图象的信息.

例2 在一条笔直的公路上有A，B两地，现有甲、乙两人同时出发：甲从A地步行匀速前往B地，到达B地后，立刻以原速度沿原路返回A地；乙则从B地步行匀速前往A地（甲、乙两人到达A地后均停止运动）.

如图3所示，图象为甲、乙两人之间的距离y（单位：m）与出发时间x（单位：min）之间的函数关系，请结合图象解答下列问题：

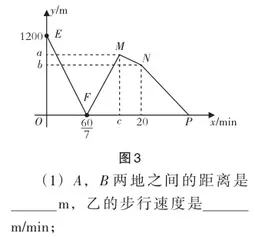
（2）求解图中a，b，c的值；（3）求解线段MN的函数解析式；

（4）在乙运动的过程中，何时两人相距80 m？

【图象分析】

下面针对一次函数的图象，采用解图“三步法”进行分析，具体如下.

第一步，看，确定坐标轴所表示的含义.坐标系的横坐标表示出发时间，纵坐标表示两人之间的距离.

第二步，找，明晰图中关键点的含义.

点E：时间为0，两人都没运动，那么两人之间的距离就是A，B两地之间的距离.

点F：纵坐标为0，即两人相遇.

点M：甲到达B地.

点N：点N前后的变化率不同，说明乙到达目的地.

点P：两人之间的距离又一次变成0，说明两人都到达A地.

第三步，变，探寻图象中变化趋势的含义.

线段EF：表示两人相向而行并相遇.

线段FM：表示两人相遇后继续往前走，两人之间的距离增大.

线段MN：甲到达B地后返回，是一个追及问题，两人之间的距离减小.

线段NP：乙已经到达A地，甲一直走向A地，两人之间的距离减小.

【过程解析】

（1）分析图象可知，开始时甲、乙两人之间的距离为1200 m.由于甲从A地出发，乙从B地出发，两人开始时的距离为A，B两地之间的距离，所以A，B两地之间的距离为1200 m.

（4）设经过x min两人相距80 m，两人相遇前和相遇后都可相距80 m.

相遇前：1200-（60+80）x=80，解得x=8；

评析：上述为元素共用图象型一次函数行程问题，探究解析时同样采用了解图“三步法”——解析图象确定两人之间的距离变化情况，后续采用待定系数法求解析式，联立方程求解点的坐标.

写在最后

一次函数行程问题充分体现出了一次函数知识的应用，使用解图“三步法”解析问题时，要注意把握图象中点、线的变化，理解其背后的实际意义.教学时，教师应注意一次函数行程问题的分类探究，引导学生关注问题特征，掌握分步解析图象的方法、思路.