转换视角,变化思维

[摘  要] 初中数学解题中需要思维的深刻性，也需要思维的灵活性. 思维的灵活性源于视觉的转换，选择特殊情形、特殊状态、特殊点会将问题具体化，从而找到解决问题的突破口;选择整体视角，容易抓住动态本质，化抽象为直观，有利于问题直接解决.

[关键词] 特殊;一般;微观;宏观;本质

原题呈现

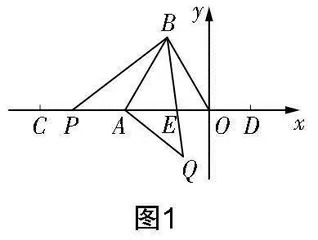
（重庆八中初2023级练习题）如图1所示，O为平面直角坐标系的原点，点A在x轴上，△OAB是边长为4的等边三角形. 已知点C（-8，0），D（2，0），P是线段CD上一点，连接BP，将线段BP绕点B逆时针旋转60°得到线段BQ，连接AQ. 在点P从点C运动到点D的过程中，线段AQ扫过的面积为______.

运用“从特殊到一般”的思路探究、

解决问题

（一）探究点Q的轨迹

1. 猜想点Q的轨迹是一条直线

遵循几何探究的一般思路——先猜后证. 由题目的已知条件可知，点P的运动轨迹是线段CD，在运动过程中∠PBQ是定值，始终是60°，而且BP=BQ. 点P的运动轨迹直接影响或制约点Q的轨迹，所以有理由猜想点Q的运动轨迹是在一条直线上.

2. 关注特殊点，发现点Q的轨迹过原点O

先由特殊点入手，结合已知条件，比较可能的四个特殊点C，A，O，D，很容易发现只有点A最特殊. 理由是，当点P与点A重合时，将线段PB绕点B逆时针旋转60°，点P的对应点即点Q就与点O重合. 从而可确定点Q的运动轨迹是在过点O的直线上.

3. 取任意点，论证点Q的轨迹为过原点O的定直线

而过点O的直线有无数条，所以，仅发现点Q的轨迹过点O并不能准确确定其轨迹. 而且上述情况是特殊情况，所以必须选择一般情况进行探究. 在线段CD上任意选择一点P，如图2所示，连接OQ. 容易发现在△PBA与△QBO中，PB=QB，∠PBA=∠QBO，AB=OB，所以△PBA≌△QBO. 所以∠BPA=∠BQO. 又∠PEB=∠QEO，所以∠PBE=∠QOE=60°. 尽管点Q是动点，但∠QOE=60°是定角. ∠QOE为定角的意思是直线QO为一条定直线. 由此可以确定点Q的轨迹在过原点且与x轴的夹角为60°的一条直线上，即图2中QO所在的直线.

4. 特殊与一般结合，确定点Q的轨迹为过原点O的定线段

显然，由点P的起点便可确定点Q的起点，由点P的终点便可确定点Q的终点. 由此可得，点Q的轨迹是线段QQ，如图3所示. 线段QQ过原点O，∠QOD=60°.

（二）解决问题

1. 先定形——线段AQ扫过的图形

问题是“线段AQ扫过的面积为______.”其中点A是定点，动点Q的轨迹是线段QQ，所以线段AQ扫过而形成的图形是△AQQ.

2. 再定量——线段AQ扫过的图形面积

上述解答过程是一般思维产生的解题思路，不仅有一定的思维难度，而且过程繁杂. 所以，很有必要探究更简洁的思路和解法.

化抽象为直观，运用整体思想

解决问题

哲学告诉我们，整体和部分可以相互转化，也可以理解为微观和宏观可以相互转化. 微观往往具有本质属性但抽象，宏观往往具有直观、形象的特征，但不易揭示本质属性. 如果把几何中的点视为微观，那三角形等几何图形就可视为宏观，介于二者之间的线段则可视为中观. 在上述问题中，单纯地思考点P的运动如何牵制点Q的运动非常抽象，甚至迷茫不知所云，究其原因，点属于微观，微观本来就抽象. 破解的思路当然是把微观转化为宏观，化部分为整体，最终化抽象为直观. 其实就是转换视角，改变分析问题的角度，变化思维.

就本题而言，点P在线段CD上运动，可以理解为点P由点C向点D运动形成了线段CD，用变化的思维方式可实现将微观的点向中观的线段转化. 再分析另一重要已知条件“连接BP，将线段BP绕点B逆时针旋转60°得到线段BQ”，这一条件有两个重要信息，其一是定点B，它与前面所确定的线段CD确定了△BCD，其二是旋转，旋转的是线段BP，线段BP就是△BCD的顶点B与其对边的连线段. 在“微观转中观，中观转宏观”这一观念的启发下有下面的思路：要研究微观点Q，就转化成研究中观的线段QB;要研究中观的线段QB，就转化成研究对应线段PB;于是自然转化成研究线段PB所在的三角形，即△BCD，并研究它绕点B逆时针旋转60°所得的三角形. 三个顶点的情况分别是：点B是旋转中心，旋转后的对应点是它本身;易得点C，D的对应点分别是点Q，Q. 因此，△BCD绕点B逆时针旋转60°所得的三角形是△BQQ. 当然，CD边的对应边是线段QQ. 再由旋转的性质（图形是所有元素都绕旋转中心按相同的方向转动相同的角度），可得线段QQ过点O并与对应边CD形成∠QOD=60°.

至此，在“化微观为宏观，化抽象为直观”哲学思维的指导下，问题的关键点和难点从整体旋转的角度轻松解决. 不仅如此，我们还可以在此基础上进一步简化问题的解决.

从个别到一般，抓本质

（一）理清解决问题的本质方法

不管是运用“从特殊到一般”思想探究轨迹解决问题，还是运用“化微观为宏观，化抽象为直观”思想整体解决问题，其本质都是由点或线段的旋转联想、发现三角形的旋转，并利用旋转的性质突破关键点和难点，从而解决问题. 前者着眼于微观——点Q的轨迹，抽象程度高，难度大，过程烦琐;后者着眼于宏观——△BCD的旋转与对应关系，直观形象，难度小，过程简洁.

（二）抽象同类问题的本质特征

进一步思考，这类问题的本质特征是什么？

第一， 有一主动点，且其运动轨迹已知. 例如本题中的点P，它的轨迹是线段CD.

第二， 有一从动点，且其运动轨迹未知. 例如本题中的点Q，它的轨迹需要探究.

第三， 主动点和从动点是旋转对应点，即它们与旋转中心的连线所形成的夹角为定角.

（三）回眸中考，举一反三

当前的中考数学试题不仅考查数学基础知识、基本技能、基本思想、基本活动经验，还考查数学思维、数学核心素养，这给教学明确了导向，要求教师在平常的教学中突破思维定式，引导学生转换视角，变化思维，增强思维的灵活性，提升数学核心素养. 2023年重庆市中考数学试题中的第26题第（3）问以压轴题的方式将“转换视角，变化思维”这一观念体现得淋漓尽致.

1. 中考真题

（重庆市2023年中考数学试题第26题）在Rt△ABC中，∠ACB=90°，∠B=60°，D为线段AB上一动点，连接CD.

（2）如图6所示，以CD为边在CD上方作等边三角形CDE，点F是DE的中点，连接BF并延长，交CD的延长线于点G.若∠G=∠BCE，求证：GF=BF+BE;

2. 真题剖析

本题第（3）问是动态问题，在动态背景中找到线段CP最大时的静态图形是解决问题的关键. 具体地讲，解决本题分四层：第一，确定线段CD最短. 显然当CD⊥AB时CD最短. 第二，确定点N的轨迹. 虽然点M是动点，但是点E是定点. 又因为点B是定点，所以线段BE的长度为定值. 由翻折可得BN=BE，进而得到点N的轨迹是以点B为圆心、BE的长度为半径的圆，如图7所示. 第三，确定点P的轨迹，这是解决本题的关键. 由前文的总结可知，若将点N视为主动点，则点P为从动点，又因为点P是线段AN的中点，所以AP ∶ AN=1 ∶ 2，从而可确定点P的

3. 解后反思

确定线段CP的最大值既是本题的难点，又是破题的关键. 因为点C是定点，又要求线段CP的最大值，所以必须探究点P的轨迹. 又已知点N的轨迹，而点N，P高度关联，即点A，P，N三点共线，这看似与前文总结模型不一致，但进一步思考会发现，这与前文的模型一致，只是一种特殊情形，即两条定线的夹角为0°，也就是点A，P，N三点共线.

（四）抓住本质特征，触类旁通

1. 问题再现

如图9所示，点C是线段AB的中点，点D是平面内一点，且AC=2CD=2，连接BD，将线段BD绕点D逆时针旋转90°至ED，连接BE，AE，求线段AE长度的最大值.

2. 直击本质

数学中的哲学思维

英国著名教育家梅森（J.Mason）指出，相对于特殊化而言，一般化是困难的. 然而，一般化又是数学创造的基本形式，因为数学认知的根本目的是要揭示更为普遍、更为深刻的事实或规律. 梅森进一步指出，通过特殊化可以很好地了解所面临的问题，通过特殊化才能找出相应的一般化模式或对策，从而解决所面临的问题. 对于所得出的一般结论，应该通过进一步特殊化做出必要的检验. 郑毓信教授也提出了相关策略：由随意的特殊化了解问题;由系统的特殊化为一般化提供基础;由巧妙的特殊化对一般性结论进行检验. 笔者正是在以上观点和策略的指导下，选择“特殊点”作为问题解决的突破口，这样有利于抽象问题具体化、直观化，再从“一般点”的角度进一步论证、转化问题，从而让要解决的问题明确、明晰.

苏轼的诗句“不识庐山真面目，只缘身在此山中”蕴含的哲理是，由于观察者所处的位置不同，看问题的出发点不同，对客观事物的认识难免有一定的片面性;要认识事物的真相与全貌，必须超越狭小的范围，摆脱主观陈见. 笔者正是在此启发下，转化视角，变化思维，当面临微观的抽象问题时，转换视角到宏观整体角度将问题直观化;当面临宏观具体问题且需要把握本质属性时，转换视角到微观的角度经历抽象、归纳、论证等过程，以准确认识其本质属性.