构建“以学为中心”的数学章节复习课新模式

[摘  要] 研究者发现，同学们在章节复习时可以更好地践行“以学为中心”，进而在师生互动和生生交流中促进每个学生的发展. 文章以“一元二次方程”的章节复习课为例，通过精心备课、问题驱动和充分让学驱动教学，实现学生学习能力的发展与提高，构建“以学为中心”的数学章节复习课新模式.

[关键词] 章节复习课;以学为中心;一元二次方程

当前，数学课堂教学改革着重强调“以学为中心”，也就是倡导课堂教学需落实学生的主体地位，充分发挥学生的学习能动性，以教与学的和谐统一来促进学生的发展. 数学章节复习课对学生的综合运用能力要求较高，而学生的认知基础又参差不齐，对知识的应用也不够自然. 因此，如何上好一节章节复习课是一线教师需要深度思考的问题. 近年来，笔者在推进“以学为中心”的改革道路上进行了深入研究，对章节复习课的教学模式进行了反复试验与矫正，取得了一些进展，下面结合“一元二次方程”的章节复习，谈谈自己的一些经验和做法.

构建“以学为中心”的一元二次

方程章节复习课的实践路径

1. 问题导入，激活思维

问题1：以“用一根长是20厘米的铁丝去围一个矩形”为背景编制一个数学问题. （这是一道开放性问题，思维之门一经打开，很快就有学生提出了教师课前的预设问题“求围成的矩形面积”）

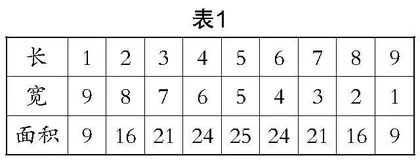
师：我们不妨来探索这个问题！（学生思考后很快有了“答案有多个”的结论，教师立即追问“有多少种可能”. 有学生进一步提出“列表展示”的方法，生成了表1）

生1：不止这些答案，因为长与宽并非只能是整数啊！

师：的确还有其他情况，那还能提出其他关于围成面积大小的问题吗？

生2：若围成的矩形面积是21平方厘米，求矩形的边长.

生3：那还不简单，表1中就展示了边长是7厘米和3厘米的情况.

生4：那可以围出面积是30平方厘米的矩形吗？

生5：可以设矩形的一条边长是x厘米，则另一条边长是（10-x）厘米，据题意可得x（10-x）=30，就这样通过设未知数列方程求解.

师：x（10-x）=30属于哪一类方程，你是根据什么判断的？（学生又一次展开思考，并通过回忆一元二次方程的定义判断该方程为一元二次方程）

师（追问）：x（10-x）=30的形式并没有如定义所述啊？

生6：可以将其转化为一般式，即x2-10x+30=0.

师：由此可见，整理后转化为一般式才能判断该方程是否为一元二次方程. 你能求解此方程吗？有几种解法？（这一问题抛出后，学生争先恐后作答，提出了配方法、直接公式法这两种解法）

师：一元二次方程有几种解法？说说每种解法的适用情况. （学生自主展开讨论）

生7：事实上，本题并不需要求解，只需要直接计算b2-4ac，由于这里b2-4ac<0，因此本题无解，即无法围成面积为30平方厘米的矩形. （直到生7解说完，其余学生才恍然大悟）

师：真是思维开阔的孩子，那可以围出面积是20平方厘米的矩形吗？（不少学生埋头计算）

师：刚才大家的探讨非常棒！在解决实际问题时，求解后检验是否符合题意是必不可少的步骤. 那可以围出面积是a平方厘米的矩形吗？（学生又一次陷入沉思，并在思考后得出“此时需要就a值究竟是多少进行讨论”的结论）

师（追问）：那什么a值可围出矩形，什么a值不可以呢？（在思考一段时间后，学生先后给出两种解决方法：方法一，列出方程并整理，之后根据根的判别式进行判别;方法二，根据配方法求a的取值范围. 教师对两种方法均予以高度肯定）

设计意图  问题的选择和设计是教学得以成功的关键一环. 课始，教师就抛出一个让学生编题的开放性问题，牢牢抓住了学生的思维与兴趣点，为之后课堂的高效推进打下了坚实的基础. 同时，这一问题在核心概念、原理、知识关联及思想方法上都体现出典型性，学生在层层推进的探索中可以很好地提炼和内化知识.

2. 拾级而上，深度建构

问题2：现将这根20厘米长的铁丝一剪为二，分别用这两段去围矩形，你能提出一个什么问题？

生9：求这两个矩形的面积和是多少. 可以是17平方厘米吗？（问题抛出后，其余学生立刻进入深入思考状态，并很快解决了问题）

生10：试求围成两个矩形的面积和的最大值. （此时，学生已经能踊跃发言，提出“一样可以用前面的配方法解决问题”）

生11：我改造了题目，把20厘米的铁丝转化成了20米的篱笆，然后把这个问题变成了一个鸡圈问题. 例如，如图1，有一段20米长的篱笆，现在靠着一面长是5米的墙围一个面积是42平方米的鸡圈，该如何围？

生12：还可以这样改，如图2，有一段20米长的篱笆，现在靠着一面长是5米的墙围一个面积是11平方米的鸡圈，并且在前面留出一扇1米长的小门，该如何围？

生13：还可以将这扇小门换到图3所示的位置.

生14：还可以像如图4这样围. （此时，课堂气氛已经达到了高潮）

师：你们真是一群思维活跃的孩子！下面就让我们一一解决以上问题……

设计意图  教师再一次层层递进地编制问题，并用开放性问题引导学生深入一元二次方程的内核进行探索，使学生在思考、探索、辨析、梳理和总结中建立知识体系，学会灵活运用知识解决问题. 在探索的过程中教师因势利导，如在编制问题时引导，在学生对问题有困惑时点拨，更多的是充分让学生在生生互动中建构知识体系，获得发展.

教学感想

相对于新授课，复习课在实践“以学为中心”上有着独特的优势，这是因为学生对相关知识有了一定认识，尽管学习上存在缺陷，但可以通过复习暴露思维过程，进而在自我剖析和反省中提高认识[1]. 同时，学生学习水平的差异性虽然客观存在，但合作学习的模式可以精准转化学困生和优化学优生，进而全面提升数学素养. 为了在章节复习中更好地践行“以学为中心”，在师生交流和生生互动中促进每个学生的发展，我们可以从以下几个方面来着手.

1. 通过精心备课改善教师的教

想要上好一节课，精心备课自然是不可或缺的，尤其是想要在章节复习课上出效果，势必需要教师用心揣摩. 备课时，教师早早定下了在复习课中让学生自主编题并解答的设想. 让学生编题并不难，但要引导学生在编题的过程中自然而然地应用所学，达到归纳提炼的效果则是有一定难度的. 当然，教师通过课前的深钻教材与具体学情，以及课中的因势利导，使得课堂朝着自己预期的方向发展，且教学也达到了预期效果，尤其是最后几个学生争先恐后地提出了具有探究价值的问题让教师十分欣慰[2]. 显然，整节课中学生的神采奕奕充分体现了他们取得收获的喜悦感，这样的课堂势必是成功的.

2. 利用创意问题引导学生的学

问题是学生思维的导火索，好的问题可以引领学生思维逐步进阶，从而促进深度学习. 本节课的设计巧妙而新颖，抛弃了传统章节复习课的一贯模式，没有梳理知识点，也没有归纳总结，仅仅是用两个开放性问题贯穿这节课，自主探究、对话交流、思维碰撞，水到渠成地梳理总结章节知识要点、建立知识体系，发展数学核心素养[3].

3. 借助充分让学促进学生发展

让学的思想就是将学生置于课堂的主体之中，教师以引导者、启发者的角色，助力学生的深度思考和探究，让学生有了更多自主学习、思考和探索的机会与平台，实现了深度学习. 本课的教学中，教师抛出问题之后千方百计地“让学”，想方设法地推动“思考”，坚持“以学为中心”，实现章节复习课的质效提升，助力学生核心素养的发展.

参考文献：

[1]沈良. 试论“知识·探究·思维”路径下学生核心素养的培养[J]. 数学通报，2017，56（10）：18-22.

[2]沈良. “大概念，大任务”视角下的数学单元教学设计[J]. 中学教研（数学），2021（07）：9-13.

[3]吕世虎，杨婷，吴振英. 数学单元教学设计的内涵、特征以及基本操作步骤[J]. 当代教育与文化，2016，8（04）：41-46.