一道几何问题“争议证法”的诊评与教学思考

［摘  要］ 学生在初学全等三角形之后，角平分线的性质定理可以简化全等判定的推理语句，这使得有些学生在问题条件中看到角平分线就过分依赖该定理的证明，反而没能从目标出发，逆向分析得出更加简明的证明思路. 教学时教师要重视向学生传递善于比较和善于优化的解题追求.

［关键词］ “争议证法”；诊评；思维回路；善于优化

在学习了全等三角形的几种判定方法之后，角平分线的性质定理也随之出现，学生才适应了全等三角形的推理语句，一下子又可以运用角平分线的性质定理简化证明过程，这使得学生往往会过分依赖这种“简化推理”，让有些本不需要运用该定理的问题出现了思维回路，反而产生了“弯弯绕”的证明语句. 本文从一道几何问题的“争议证法”说起，并给出笔者的诊评意见与教学思考，以供讨论.

从一道几何问题的“争议证法”说起

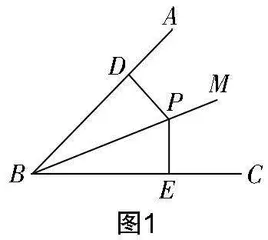
问题：如图1，已知BM平分∠ABC，点P在BM上，PD⊥BA，PE⊥BC，垂足分别为D，E. 求证：BD=BE.

学生解法：

因为BP平分∠ABC，PD⊥BA，PE⊥BC，

所以PD=PE. （角平分线上的点到角的两边距离相等）

在Rt△BPD和Rt△BPE中，BP=BP，PD=PE，所以Rt△BPD≌Rt△BPE（HL）. 所以BD=BE.

争议观点：一部分教师认为学生的以上解法是错误的，属于“循环论证”.他们的说法是：学生运用角平分线的性质定理“角平分线上的点到角的两边距离相等”证明“PD=PE”，然后再运用“HL”证明两个三角形全等，而“角平分线的性质定理”本身就是由两个三角形全等（△BPD≌△BPE）推证而来. 另一部分教师认为，学生的证明“步步有据”，应该是正确的.

诊评意见：我们认为，从逻辑性上看学生的证法是没有错误的，证明的每一步都“步步有据”. 至于有教师认为属于“循环论证”的评价是站不住的. 所谓“循环论证”，是指用来证明论题的论据本身的真实性要依靠论题来证明的逻辑错误. 如证明“轻音乐能催眠”，所用的论据是“轻音乐有催眠的力量”，而“轻音乐有催眠的力量”，又要借助“轻音乐能催眠”来证明. 这就是犯了循环论证的自证. 回到学生的证明来看，虽然最后是证明两个三角形全等，但使用的是“HL”来判定两个三角形全等，而角平分线的性质定理是运用“AAS”来推理的，两种判定三角形全等的方法并不够成“循环论证”. 我们还可将“学生证法”再换一种“等价”的证法如下：

证明：因为BP平分∠ABC，所以∠DBP=∠EBP.  因为PD⊥BA，PE⊥BC，所以∠PDB=∠PEB.  在△BPD和△BPE中，∠PDB=∠PEB，∠DBP=∠EBP，PB=PB，所以△BPD≌△BPE（AAS）. 所以PD=PE. 在Rt△BPD和Rt△BPE中，BP=BP，PD=PE，所以Rt△BPD≌Rt△BPE（HL）. 所以BD=BE.

这样来看，学生的证法就是一种典型的“思维回路”，并不是错误证法. 当然，没有错误的解法，并不一定是“好的解法”，学生的证法是典型的“弯弯绕”的证明方法，需要我们在教学时引导他们进行解法上的改进，以下给出我们的教学建议.

讲评设计：（投影展示“学生证法”）

教师提问：同学们看下这种证法能否更简捷一些？

教学预设：学生应该想到直接运用“AAS”证两个三角形全等，即可证明成功. 或者运用“等角的余角相等”证出“∠BPD=∠BPE”，再运用角平分线的性质定理，证明如下：

因为∠BPD=∠BPE，PD⊥BA，PE⊥BC，所以BD=BE.

教师点评：认真审题，寻找、接通证明思路后，要再思考一下思路是否简明，是否直接，同学们要学会减少“弯弯绕”的多余步骤.

对一些几何定理“教学顺序”的对比分析

查阅不同版本（人教版、苏科版、北师大版、华师大版等）的初中数学教材会发现，角平分线的性质定理（角平分线上的点到角的两边距离相等）分别出现在全等三角形的判定之后或者轴对称图形一章（与线段垂直平分线的性质定理一起出现）. 角平分线的性质定理一般都采用的是“AAS”判定两个三角形全等，进而明确为定理及符号语言，以方便后续简化与之相关的推理证明.

由于上文中“学生证法”出现了直角三角形全等的判定定理（HL）的运用，我们也查阅了不同版本教材中“HL定理”出现的顺序，多数教材都是紧随“SSS，SAS，ASA，AAS”的判定方法之后就直接以画图验证的方法给出“HL定理”，但又不给出推理证明——不少教材只能含糊地加上一句“这是一个定理，以后会给出它的证明（比如，人教版教材在隔了一个学期之后，待学习到勾股定理以后再以例题的形式对‘HL定理’进行了证明）”. 笔者查阅后发现我国台湾地区的初中几何教材则将“HL定理”安排在等腰三角形的学习之后（即学生掌握“等边对等角”“等角对等边”的定理），其证明如下：

“HL定理”及证明：如图2，已知在△ABC和△A′B′C′中，∠ACB=∠A′C′B′=90°，AB=A′B′，AC=A′C′. 求证：Rt△ABC≌Rt△A′B′C′.

证明：把△ABC与△A′B′C′拼在一起，使相等的直角边AC与A′C′重合，并使点B，B′在AC边（A′C′）的两旁.

因为∠ACB=∠A′C′B′=90°，所以∠B′C′B=2∠ACB=180°. 所以点B′，C′，B在同一直线上.

在△A′B′B中，因为A′B′=AB=A′B，所以∠B=∠B′（等边对等角）.

在△ABC和△A′B′C′中，∠ACB=∠A′C′B′，∠B=∠B′，AB=A′B′，

所以△ABC≌△A′B′C′（AAS）.

简评：可以发现，如果“部分教师”只看到现行的人教版教材上的几何内容呈现顺序，对于上述“HL定理”的证明方法，是不是也会认为是一种“循环论证”？这也提醒大家，如果只是关注手头这一本教材，并把它当成“唯一依据”，“敬如神明”，显然不是一种科学的态度.教师应该站在几何知识逻辑结构的高度来认识、理解教学内容所在逻辑链条的位置，从而让自己对一些教学疑惑、争议问题看得更加通透、明晰.

解题教学要注重“比较和优化”

第一，对学生解法不能止于判断“对与错”

在当前“双减”背景下，很多学校对教师批改作业提出了“精批细改”的要求. 我们认为，“精批细改”有一个内涵就是不能止步于判断学生解法的“对与错”. 具体来说，以上文提及的“学生证法”为例，这种证法虽然不能被认为是错误解法，但教师应该对这种证法写出必要的点评（证明过于烦琐，“弯弯绕”），并要求学生进行优化和订正. 同样，在课堂教学中，对学生的一些解法或思路，教师在倾听理解之后，也可组织学生进行分析和比较，让学生知道数学解题不仅要关注结果，还要注意过程的简化、表达的优化［1］.

第二，解题教学中要重视从纠错走向究错

数学解题教学离不开纠错，善于纠错并帮助学生答疑解惑是每个数学教师需要修炼的教学基本功之一. 课堂教学中，“捕捉”学生的错误资源，并将这种“生成性资源”化用在教学进程中，带领学生从纠错走向究错，正是小学著名特级教师华应龙老师所主张的“化错教学”［2］. 我们也常常看到一些经验丰富的教师在解题教学中总会设置一两处纠错的教学环节，通过这些化错教学的场景运用，教师会先稚化自己的思维，装作看不懂、看不出学生的错误，激发学生参与纠错、优化的学习兴趣，往往能取得很好的教学效果.

第三，思路贯通后要让推理表达更加简明

多年之前，郑毓信教授曾在《人民教育》发过一组关于数学教师“三项基本功”（善于举例、善于提问、善于优化）［3］的文章，其中关于“善于优化”的相关论述中，郑教授特别指出教师要向学生传递“善于比较和优化”的教学思想. 比如，本文开篇关注的角平分线的基本问题中，当“学生证法”出现后，教师要再挑选一些更加简明的方法进行对比分析，让学生在对比中发现“更初等”（相较于角平分线的性质定理来看，直接运用AAS证明全等的思路是“更初等”的）的解法、更简明的解法.

写在后面

本文从一些教师面对学生的“争议证法”说起，通过查阅不同版本教材中一些几何定理出现的“序”，思考了与这些定理相关的解题教学过程中的思路和推理语句的优化. 有些想法可能比较个性化，还缺少广泛讨论，期待更多同行的深入研讨，使大家对相关问题理解得更加透彻.

参考文献：

［1］潘荣菲. 展望新加坡2013年中学数学课程［J］. 数学教学，2012（08）：1-3.

［2］华应龙. “化错教育”的实践根基与文化底蕴［J］. 江苏教育，2020（78）：15-18.

［3］郑毓信. “数学教师的基本功”之三 善于优化［J］. 人民教育，2008（20）：43-44.