关注综合能力培养 提升数学核心素养

作者简介：高洁（1978—），本科学历，中学一级教师，从事初中数学教育教学工作.

[摘  要] 当下，在素质教育的推动下，教师应不断更新教学观念，采用多样化的教学手段和教学模式来发展学生的自主学习能力，提升教师的教学素养. 在初中数学的教学过程中，教师应重视学生综合能力的培养，通过听、说、读、写、画等方式来训练学生的数学能力，综合提升学生的学力，从而落实学生的数学核心素养.

[关键词] 综合能力;综合训练;数学核心素养

初中数学教学除了传授知识而外，还应采用多样化的教学手段帮助学生积累数学活动经验，提高学生独立分析问题和解决问题的能力. 在日常教学过程中，教师要重视学生听、说、读、写、画等综合能力的培养，要通过多元化的教学活动来提升学生参与课堂的积极性，活化课堂. 不过，在实际教学中，部分教师片面地认为数学教学就是解题教学，为了追求解题常常忽视学生听、说、读等综合能力的训练，进而影响学生学习能力的提升. 下面笔者结合教学经验，浅谈培养学生听、说、读、写、画综合能力在落实学生数学核心素养方面的价值，以期抛砖引玉，引起同行的共鸣.

重视听说训练，培养抽象概括

素养

倾听是一种习惯，更是一种能力. 教学过程中学生不仅要认真地听教师讲，还要听同学说，同时认真思考，以此不断提高自己分析问题和解决问题的能力. 教学中，为了让学生认真听，教师可以结合教学内容和学生学情设计一些可操作的要求，从而培养学生的专注力，提升学生的听课效率. 另外，在教学中，教师要提供时间让学生思考，并创造机会让学生进行互动交流，以此培养学生的合作意识，提高学生的数学表达能力. 在实际教学中，很多学生将“说”理解为大胆地表达和响亮地回答，其实这只是一种表现形式，“说”应该建立在“思”的基础之上，因此教师应指导学生认真地倾听与思考，以确保“说”时完整、正确.

例如，刚接触几何图形时，学生由于空间观念和直观想象能力相对薄弱，因此在学习中容易出现畏难情绪. 为了改变这一现状，教师可以利用现代多媒体技术直观、生动的特点，通过演示图形变幻万千的形态来激发学生的学习兴趣，培养学生的空间观念. 当然，通过演示调动学生参与的积极性之后，教师还应在学法上进行指导，在倾听中激发学生的探究欲，以此诱发学生思考、交流，提升课堂教学效果. 学生理解相关概念后，教师还应鼓励学生结合生活经验说一说自己眼中的几何图形及用处，并通过由抽象到具体的转化唤醒学生对几何学习的兴趣. 同时，通过积极思考、交流和表达，还可以锻炼学生的语言表达能力，提高学生的数学素养.

当然，在教学过程中，教师不仅要引导学生倾听，自己也要善于倾听，要在互动交流中了解学生的所思、所想、所惑，并通过行之有效的引导让学生主动参与到课堂教学中，以提高课堂教学的有效性.

重视读写训练，培养逻辑思维

能力

在唯分论的束缚下，“刷题”成了学生课后数学学习的主旋律，阅读似乎是可有可无的. 然阅读有利于提高学生的交流能力，有利于提升学生的语言水平，有利于激发学生的数学学习兴趣，因此在初中数学教学中，教师也要重视学生阅读能力的培养. 从调研中不难发现，“刷题”虽然在一定程度上可以帮助学生积累解题经验，提升解题效率，但从长远发展来看，机械地“刷题”容易造成思维定式，会消耗学生的数学学习热情，影响学生思维能力的发展. 在数学教学中，部分师生对阅读的理解不够全面，认为培养阅读能力是语文教学的事情，数学最主要的就是解题，因此在数学教学中依然延续着“题海战术”. 但是从教学实践中不难发现，那些数学成绩好的学生，其阅读能力非常强，审题又快又准;而那些成绩相对落后的学生，他们常常因读不懂题意而在解题时漏洞百出，影响解题效果. 因此，在数学教学中培养学生的阅读能力应是一项重要的教学任务. 数学阅读与语文阅读有所不同，数学阅读不能采取快速阅读法，而应细读，理清上下文的关系，以此提升学生的逻辑思维能力.

例如，教学“有理数的乘方”时，教师没有直接讲授，而是预留时间让学生阅读教材，并思考如下问题：（1）什么是乘方？（2）什么是指数和幂？（3）乘方的运算法则什么？学生带着问题边阅读边思考，不仅能提高阅读积极性，而且能通过有效阅读提炼有价值的信息，以此锻炼抽象概括素养，提升自主学习能力. 学生阅读后，教师还可以鼓励学生进行小组探究，让学生在互动交流中得到明确的问题答案，以锻炼学生的语言表达能力，增强学生的合作意识.

此外，在日常教学中，教师还应重视学生的数学书写训练，要通过规范书写提高学生的数学领悟力，培养学生思维的严谨性，强化学生对数学概念、定理等基础知识的理解与记忆，有效避免因思维漏缺出现的不规范书写，切实提高学生的数学应用能力.

读写相结合的方式，不仅可以提高学生的思维品质，而且可以提高教学效率，有利于“教”与“学”全面提升.

培养画图识图能力，提高解题

效率

数形结合是重要的数学思想方法，是提升解题效率的重要武器. “数”与“形”的有机结合，既能帮助学生获取有用的数学信息，又能丰富学生的认知，帮助学生快速地形成解题方法，从而提高解题效率. 读图是一种基本能力，通过读图，学生不仅可以获得有用的数学信息，还能进一步强化“双基”，提高解决问题的能力. 另外，解题时除了读图以外，教师还要指导学生正确画图，帮助学生获得正确的解题思路. 教学中，教师在指导学生画图、识图和解图的过程中，既要重视挖掘图形中有价值的信息，又要有意识地引导学生进行数形转化，以达到简化题意、提高解题效率的目的.

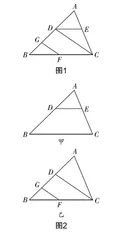
例如，在学生解读图1的过程中，教师可以引导学生将这一复杂图形进行拆分，转化为如图2所示的两个基本图形. 如对于图2中的甲图，由DE，BC两条平行直线被直线AB，AC所截，可以得到多对同位角;对于图2中的乙图，由GF，CD两条平行线被直线BA，BC所截，同样可以得到多对同位角. 通过拆分将复杂图形转化为基本图形，实现了图形的简化，能让学生轻松地获得许多有价值的信息，从而为问题的解决提供便利.

另外，在数学学习中，除了识图以外，教师还要教给学生画图的方法，指导学生精准地画图，并让学生进行反复练习，以提高学生的画图水平. 不过在解题过程中，有些学生画图时常常是草草了事，这样不仅难以通过读图提炼有价值的信息，而且容易干扰思路，影响解题效果. 因此，在教学中，教师必须重视学生画图能力的培养，使学生借助图形让问题顺利获解.

例如，解决关于角平分线的问题时，一般题设中不会明确地给出该角是多少度. 一般情况下，画图时会将该角画成锐角或者钝角，再画角平分线（如图3所示的甲、乙两图）. 对于图3丙图，OC显然不是∠AOB的平分线;对于图3丁图，OC是直角∠AOB的平分线.

相信通过以上画图训练，学生不仅能掌握一些画图的基本技巧，而且能深化对角平分线概念的理解，同时能为日后探究角平分线的性质做铺垫. 在以上画图、看图和读图的训练中，教师之所以给出图3丙，目的是让学生通过辨析感悟精准画图的意义，以此培养学生良好的画图习惯.

其实，不仅解决几何问题需要画图，解决一些代数问题也需要画图，通过画图，我们能发现蕴含其中的数量关系，由此找到解题灵感，从而顺利地解决问题.