基于“5E”教学模式，培养核心素养

[摘  要] 教学设计是落实核心素养的关键环节，其有效落实需要合适的教学模式. 由美国生物学课程研发中心提出的“5E”教学模式遵循了学生的认知规律，强调“以学生为主”及让学生进行科学探究，是一种有效的探究式教学模式[1]. 文章将“5E”教学模式应用于“点的位置与坐标”第一课时，通过“活动+问题串”引导学生全程参与课堂教学. 课后对学生进行了问卷调查，分析相关数据可知：“5E”教学模式对学生数学核心素养的培养确有帮助.

[关键词] “5E”教学模式;点的位置与坐标;活动课;教学设计;核心素养

问题的提出

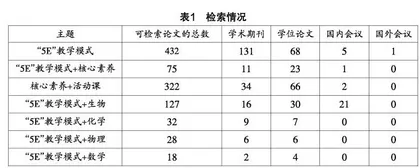
1989年，美国生物学课程研究中心（BSCS）研发出了符合当代实际教学的教学模式——“5E”教学模式，其包含5个主要环节，分别是吸引（Engagement）、探究（Exploration）、解释（Explanation）、迁移（Elaboration）和评价（Evaluation），因各个环节的名称均以字母“E”开头，故简称“5E”教学模式. “5E”教学模式历经30多年的研究与发展，实践表明其在一定程度上能够促进学生的学习兴趣和学习结果，同时为培养学生核心素养提供了实可参考的实践素材[2]. 为进一步了解“5E”教学模式在国内的研究现状，在中国知网围绕相关研究内容进行了检索，检索情况如表1所示.

由数据可知，“5E”教学模式与核心素养的关系存在着相当大的研究价值，核心素养与活动课的关系可以近似地看作是目标与途径的关系. 所以，对于中学数学学科，三者（“5E”教学模式、核心素养、活动课）之间的关系必然存在着研究价值.

在高级检索中以主题“‘5E’教学模式+数学”进行检索，共有18篇文献可供参考，时间跨度为2014年至2021年. 可见，“5E”教学模式在数学领域中的研究较晚且成果不多，相关研究成果主要分为以下三类：

（1）理论层面.李欢从“5E”教学模式的内涵出发，得出该模式是一种旨在引起学生学习兴趣的教学模式，在了解学生的前科学概念和培养学生的数学探究能力等方面极其有效[3].

（2）教学实践方面.黄一娉将“5E”教学模式运用于高中数学复习课的实验教学环节并得出：“5E”教学模式可以使实验班学生的数学学习成绩显著改善，对学生的数学理解、问题解决、情感态度、学习方式、思维水平等方面都产生了积极的影响[4];陈算荣、陈建祥和郑兆圣应用“5E”教学模式对“锐角三角函数”进行了教学设计和教学实践研究，实践结果表明该模式的5个环节与教师教学过程的5个层次相对应[5];洪玉以“函数”和“对数”为例，应用“5E”教学模式对高中数学概念课进行了教学实践研究，对“5E”教学模式的各个环节给出了教学指导，给出了该模式应用于课堂教学的两个基本条件[6];程琳应用“5E”教学模式引导小学生探究学习，指出在小学数学教学中有效地应用“5E”教学模式可以激发学生的学习兴趣，帮助学生掌握数学知识，提高教学质量[7].

（3）课例展示方面.黄一娉、黄梦远和唐剑岚基于“5E”教学模式对数学实验课进行了教学设计[8];侯煜群以“直线与平面平行的判定”为例展示了“5E”教学模式在数学中的应用[9];龙非凡和周莹以“勾股定理”为例进行了教学设计，给出了“5E”教学模式在数学教学中的应用策略[10].

综上，国内关于“5E”教学模式在数学领域的研究范围从小学到高中，课型有复习课、概念课、实验课、定理课等，目前尚未出现活动课. 所以，文章选择将“5E”教学模式放入中学数学活动课. 原因如下：

（1）活动课提供了丰富的活动经历和思维材料，是发展数学核心素养的有效载体.

（2）活动课可以引导学生进行数学活动，重视学生提出问题和解决问题的整体过程，提倡深度学习、积极反思[11]，这与“5E”教学模式的教学环节相契合.

所以，将“5E”教学模式、活动课、核心素养联系在一起，探讨三者之间的关系，对学生数学核心素养的培养有一定的研究意义.

总体教学分析及设计

“点的位置与坐标”作为第一课时，选自北师大版八年级上册的数学教材;主要内容为平面直角坐标系的建立，使点与数的对应关系实现由一维到二维的过渡，这将为用代数方法研究几何问题提供重要的数学工具.

学生在小学已经学过“用数对表示位置”，所以本节课对学生来说并不陌生;但对于中学生，由此出发抽象出平面直角坐标系的思维活动并不简单，故将其设计为一节活动课是合适的. 这可以起到概念阐述直观生动、表象鲜明，思维表达具体可见、清新自然的作用，让学生形成良好的数学直觉极为重要;同时可以调动学生的手、脑、眼，利于培养学生的综合思考能力.

具体的教学目标如下：

（1）理解平面内点的坐标、平面直角坐标系等概念;根据平面直角坐标系写出点的坐标，根据点的坐标确定点的位置，明确点的坐标与点的位置一一对应的关系;能结合具体情境，灵活运用多种方式确定点的位置;理解平面直角坐标系内特殊点的坐标特征.

（2）经历平面直角坐标系建立的过程，在具体的活动中感受特殊点的坐标特征，进一步发展数形结合思想.

（3）通过亲身参与四个活动，感受数学来源于生活又服务于生活.

课前准备：

（1）教室准备：将单人桌合并排列，使其前后左右间隔距离相等.

（2）教具准备：投影仪一台，磁性黑板一块，PPT7张，两根装有箭头的长绳且标有字母x，y，表示数轴上点的坐标的数字卡片若干（0，±1，±2，±3，±4，…）.

活动形式：

把教室地面作为平面直角坐标系，每位学生的座位作为平面内的一个点，组织4次活动，研究平面内点的位置与坐标.

具体教学过程及解读

1. 吸引（Engagement）

“5E”教学模式的吸引环节要求教师创设与学生现实生活贴近的问题情境，引起学生的认知冲突，使学生暴露出现有的知识水平.

创设情境1：母亲节那天，小丽同学的母亲的单位准备发放电影票，有两部电影可供选择：一部是母亲期望已久的生活片《八月》，一部是小丽心心念念的《哈利波特》，但每人只能领取一张电影票，你们猜测小丽同学的母亲领了哪一张电影票？为什么？

教学处理：小组讨论后，请学生举手选择;大多数学生认为小丽同学的母亲领取的是《哈利波特》，原因是大多数学生“以己母之所好，推及人母之所好”.

师：大多数同学回答得正确，母亲为小丽领取了一张电影票. 请同学们想想：小丽到达电影院后会怎么找到自己的座位呢？

教学处理：这是本节课要处理的关键问题，给学生充分的思考时间和表达时间，不急于判断对错.

设计意图  短短3分钟，在不影响课程进度的情况下，能使学生感受到母爱亲情的教育，同时明确平面内确定点的位置需要两组数据，激发学生解决问题的欲望，帮助学生进入新概念的学习.

2. 探究（Exploration）

“5E”教学模式的探究环节要求教师根据学生现有的概念认知、过程认知及技能，创设一个共同的任务，让学生通过操作或实验，运用原有知识形成新概念、产生新方法，探索新问题和可能产生的结果.

探究活动1：

师：请同学们以竖排为列，横排为行，有序地排成六列七行，具体规则如图1（a）所示;接着用两根标有x，y的长绳，以第四行、第三列所在直线分别为x轴、y轴，将教室建立成一个平面直角坐标系，如图1（b）所示.

师：比较第二行第三列位置上的学生与第三行第二列位置上的学生，他们是同一人吗？在平面直角坐标系内，怎样表示两位同学所在位置的坐标呢？

教学处理：让学生带着问题进行探索，发现两个位置上的不是同一人;便于区分，教师引导学生分别用有序数对（3，2）与（2，3）表示，同时讲解点的坐标的概念.

探究活动2：

师：在建立的平面直角坐标系内，设每位同学表示一个点，每两位同学之间间隔一个单位长度.

师：接下来请每位同学依次报出自己位置的坐标.

活动完成后，教师随机说出一个坐标，学生要迅速说出该位置（坐标）上的人是谁.

设计意图  将课本上广播操的队形换成教室中的座位，使学生身临其境，获得一定的感性认识;从第二行第三列位置上的学生与第三行第二列位置上的学生的区别，突出在平面上用有序数对表示位置的合理性. 设置活动：请学生报出自己位置的坐标，以及教师给出坐标让学生寻找对应的同学，进而达到本节课的教学目标.

3. 解释（Explanation）

“5E”教学模式的解释环节要求学生解释自己对概念的理解，教师的解释引导学生步入深层次理解.

师：（在图2的投影下）请同学们为坐标轴、坐标原点、平面直角坐标系、点的坐标下定义.

教学处理：组织学生先小组讨论，请小组代表发表看法，小组的其他学生进行补充及修正;针对学生回答的情况，教师加以补充，使学生形成正确的概念;初次介绍象限的概念，用PPT展示概念.

设计意图  解释环节给了学生思考、反思本质的机会，学生需要进一步理解概念.

探究活动3：

师：（了解了象限的概念之后）请在第一象限的同学站起来，每人说出表示自己位置的坐标，再回答你们所在象限的坐标有什么特征. （第二象限以此类推）

师：想一想，第三象限内点的坐标有什么特征？请在第三象限的同学站起来，检验前面的结论是否正确.

全班共同探讨第四象限内点的坐标的特征，并让学生站起来加以验证.

师：请位置在x轴上的同学站起来，观察其坐标有何特征;请位置在y轴上的同学站起来，观察其坐标有何特征.

教学处理：请学生大胆说出自己的想法，其他学生和教师一起补充和修正，最后用PPT呈现总结.

设计意图  采用小组讨论和亲身实践，确保所有的学生都能参与其中，使学生在轻松的学习氛围中了解四个象限内点的坐标的特征，突破并掌握坐标轴上点的坐标的特征这个教学难点;最后教师给出标准答案，让学生明确自己的回答不足.

探究活动4：

师：在我们中有满足这样坐标的同学吗？坐标为（1，1），（2，2），（3，3），（-2，-2），（0，0），请你们站起来并想一想你们所站的位置在哪个象限内.

师：第二、第四象限的角平分线上的点的坐标有什么特征呢？

师：请横坐标是“2”的同学站起来，观察其位置有何特征;请纵坐标是“-2”的同学站起来，观察其位置有何特征.

想一想，试一试：将两根表示数轴的绳子的交点换一个位置，你的位置变化了吗？你所在位置对应的坐标变化了吗？

教学处理：学生给出答案后，教师加以鼓励，同时指明今后为了研究数学问题，可以选择适当的位置建立平面直角坐标系.

设计意图  解释环节聚焦了前两个环节（吸引环节和探究环节）的某个具体方面，为学生提供了机会去说明自己的概念性认识、方法技能或行为，强调学生是学习的主体，教师只是教学的引导者. 利用探究活动3和探究活动4，使学生在亲身参与的过程中为各个概念下定义，掌握平面直角坐标系的特征.

4. 迁移（Elaboration）

1976年7月28日凌晨，我国河北省唐山市发生了里氏7.8级的大地震，这次地震造成242769人死亡，164851人重伤，位列20世纪世界地震史死亡人数第二. 地震中心位于东经118.2°，北纬39.6°. 你能在地图上找出地震中心的大致位置吗？