追根溯源助解题 正本清源促发展

[摘  要] 以2018年北京市中考第27题的深度分析、流畅解决和适度拓展为例，强调了“四基”的整体性和统一性，明确提出培养学生的数学直觉和发展学生的数学思维应该成为平面几何教学的重要目标;揭示了数学直觉在引领学生产生联想与发现问题本质之间的联系，数学思维在促进学生形成证明思路、深化问题本质理解过程中的重要作用;阐明了指导学生归纳梳理、提炼概括蕴含于解题过程之中的数学基本思想和基本活动经验对于发展学生数学核心素养的重要教育价值.

[关键词] 追根溯源;正本清源;数学直觉;数学思维

推理是数学最为显著的特征之一，也是数学内部自身发展的依赖，更是一种基本的数学思想[1]. 数学的推理是一种有逻辑的推理，其过程基于数学的直觉和思维. 因此，学习数学的要义不仅仅是为了认识和理解概念定理、公式法则等基础知识，也不仅仅是要掌握“会计算”“会证明”的基本技能，更重要的是指导学生在“感悟”和“理解”的基础上，最终形成数学的直觉和数学的思维. 这一点完全符合《义务教育数学课程标准（2011年版）》所倡导的要注重“四基”、突出强调基本思想以及基本活动经验的本意[2]. 这就要求教师必须立足学生的数学直觉培养和思维发展来开展平面几何的教学设计与实施. 下面，笔者以2018年北京市高级中等学校招生考试数学试卷第27题为例，谈谈这方面的思考与研究.

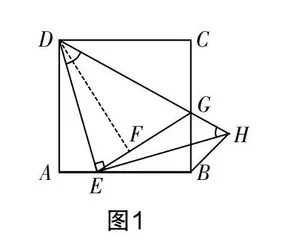
问题呈现 如图1所示，在正方形ABCD中，E是边AB上的一动点（不与点A，B重合），连接DE，点A关于直线DE的对称点为F，连接EF并延长交BC于点G，连接DG，过点E作EH⊥DE交DG的延长线于点H，连接BH.

（1）求证：GF=GC;

（2）用等式表示线段BH与AE的数量关系，并证明.

追根溯源

上述问题中的第（1）问是求证两条线段GF与GC相等，比较简单，只要连接DF（如图1所示），则容易证明△DAE≌△DFE，随即可证得∠DAE=∠DFE=90°，DA=DF. 进而容易证明Rt△DFG≌Rt△DCG，于是GF=GC得证. 下面我们重点分析和解决第（2）问.

1. 问题分析

学生在解决第（2）问的时候会遇到困难，虽然已知条件正方形ABCD中、DE⊥EH等都不难理解，但是对于射线BH与正方形ABCD的位置关系，学生还不能准确把握，从而不能产生准确的联想和正确的解题思路.

事实上，学生在以前的练习中是见过本题的影子的，但只是见过类似的问题还不一定能使学生在遇到一个新问题的时候自然地产生十分精准的联想. 正因如此，著名的美国数学教育家波利亚（G.Polya）在《怎样解题》中给出了指导解题的“解题表”，表中罗列了若干问题和解题建议，旨在驱动解题者基于已有认知自然而然地产生丰富而准确的联想.

例如，波利亚在解题表中给出过这样的问题：

你以前看过此题吗？是否见过形式略有不同的题目？

基于已知问题，如果学生能够进行上述自我追问，或许可以促使自己联想到与该问题类似的问题：

类似问题 如图2所示，在正方形ABCD中，点E在边AB上，EH⊥DE，与∠CBA的外角平分线交于点H. 求证：DE=EH.

上述类似问题有多种证明方法，前几年中考也考过，而且该题还可以推广到任意正多边形的情形.

在图2中，由于DE⊥EH，且DE=EH，所以△DEH为等腰直角三角形，BH为∠CBP的平分线. 而在图1中，如果E不是边AB上的动点，而是定点，那么猜想BH与AE的数量关系将变得易如反掌.

由此可以看出：图2与图1主体结构相同，且图2之题是图1之题的“根”，找到了问题的“根”，“树干、树枝和树叶”也就可以看得更加真切，解题思路也就可以自然而得. 应该说，追根溯源可以助力我们产生准确的联想、发现问题的本质并形成正确的解题思路.

2. 流畅解题

基于上述类似问题的研究，学生解决中考27题的思维过程可以分为如下三个阶段：

第一阶段：要先证明DE=EH;

第二阶段：要能够根据联想到的类似问题，想到证明BH为∠CBA的外角平分线;

第三阶段：把与BH有等量关系的线段和线段AE放在同一个三角形中，进而要能够大胆猜想BH与AE的数量关系，最后证明猜想即可.

下面，笔者先给出前两个阶段的证明过程，进而多角度阐述第三阶段关于猜想的证明.

【第一阶段：证明DE=EH.】

如图3所示，由（1）知△DAE≌△DFE，所以∠1=∠2. 因为△DFG≌△DCG，所以∠FDG=∠3.

在正方形ABCD中，因为∠1+∠2+∠FDG+∠3=90°，所以∠2+∠FDG=45°，即∠EDH=45°.

又∠DEH=90°，∠EHD=45°，所以△DEH为等腰直角三角形.

所以DE=EH.

【第二阶段：证明BH为∠CBA的外角平分线.】

延长AB至点P，连接DB，则有∠CBP=90°，∠DBE=45°，所以∠DHE=45°.

所以 D，E，B，H四点共圆.

所以∠HBP=∠EDH=45°.

所以∠HBC=45°，即BH为∠CBP的平分线.

说明 从上面的证明过程我们看到，本题要证明的是两条线段的数量关系，但需要先确定这两条线段的位置关系，基于位置关系再确定数量关系，即先定“位”再定“性”最后再定量;由于线段BH在△EBH中，而EH（EH=DE）也在△EBH中，所以∠HBP=45°，∠EBH=135°，∠HBP=∠BEH+∠EHB=45°等为确定BH与AE的数量关系准备了条件. 下面重点阐述第三阶段的证明.

【第三阶段】

思路1 构造全等三角形.

证法1 如图4所示，在AD上截取AK=AE，则△KAE为等腰直角三角形，∠AKE=45°.

所以∠EKD=∠HBE=135°.

因为∠DEH=90°，所以∠2+∠AED=90°.

又∠1+∠AED=90°，所以∠1=∠2.

又DE=EH，所以△EKD≌△HBE. 所以BH=EK.

在Rt△AEK中，EK=AE，所以BH=AE.

证法2 如图5所示，连接BD，过点E作EK⊥AB交BD于点K，则△KEB为等腰直角三角形. 所以KE=BE.

因为∠2+∠AED=90°，又∠1+∠AED=90°. 所以∠1=∠2.

又DE=EH，所以△HBE≌△DKE. 所以BH=DK.

过点K作KL⊥AD于点L，则△DLK为等腰直角三角形. 所以DK=LK.

易证四边形LAEK为矩形，所以LK=AE. 所以BH=AE.

说明 证法1和证法2都是直接利用了△HBE，所以证明过程简洁顺畅，下面间接应用△HBE，与证法1、2比较，会有异曲同工之妙.

证法3 如图6所示，过点H作HK⊥BP于点K，则△HKB为等腰直角三角形，所以BH=HK.

在Rt△DAE和Rt△EKH中，∠1=∠2，DE=EH，所以Rt△DAE≌Rt△EKH. 所以AE=HK.

所以BH=AE.

证法4 如图7所示，过点H作HP⊥BH交AB的延长线于点P，则△BHP为等腰直角三角形，所以HP=HB.

延长DA到点K，使AK=AE，则△AKE为等腰直角三角形. 所以KE=AE.

因为∠1=∠2， ∠DKE=∠EPH=45°，又DE=EH，所以△DKE≌△EPH.

所以HP=KE=AE.

所以BH=AE.

思路2 构造平行四边形.

证法5 如图8所示，以点A为旋转中心，将Rt△DAE顺时针旋转90°，使DA与AB重合，得到Rt△BAK. 连接AC，KE，则△AKE为等腰直角三角形.

所以∠1=∠2=∠3. 所以KE∥AC∥BH.

因为DE⊥EH，DE绕点A旋转90°到KB， 所以EH∥KB.

所以四边形EKBH为平行四边形.

所以BH=KE.

又KE=AE，

所以BH=AE.

思路3 应用四点共圆.

证法6 如图9所示，由前面的证明可知，D，E，B，H四点共圆，作出辅助圆☉O， 与AD的另一个交点为K，连接KE，KH，则∠1=∠3.

因为∠1=∠2，所以∠2=∠3.

所以KH∥EB，BH=EK.

所以∠A=∠AKH=90°.

又∠EKH=∠EDH=45°，所以∠AKE=45°.

所以△AKE为等腰直角三角形.

所以EK=AE.

所以BH=AE.

思路4 应用解三角形法.

证法7 如图10所示，在Rt△DAE中， sin∠1=.……①

在△EBH中，应用正弦定理，得=.……②

因为sin∠EBH=sin135°=sin45°=，sin∠1=sin∠2=，又DE=EH， 所以由①和②，得=.

所以BH=AE.

说明 采用解三角形的方法解决平面几何证明问题，基本思路就是将证明转化为计算.这种方法不用添加辅助线，过程清晰而简捷，对于学有余力的同学（例如，参加过初中数学竞赛）就像是打开了一扇窗，拓宽了几何问题的证明路径.

思路5 应用解析法.

证法8 建立如图11所示的平面直角坐标系，设A（0，0），B（a，0），C（a，a），D（0，a），E（b，0），则直线DE的解析式为y=-x+a，又因为DE⊥EH，所以直线EH 的解析式为y=（x-b） .……①

直线BH 的解析式为y=x-a.……②

解由①和②联立的方程，得x=a+b，

y=b.所以H（a+b，b）. 所以BH=b.

因为AE=b，所以BH=AE.

说明 在初中学习一次函数y=kx+b（k≠0）的基础上，根据两条直线平行和垂直的条件，利用解析法证明具有垂直或平行关系的直线型平面几何问题，简单易行. 本题就是利用了正方形中DE和EH的垂直关系，将问题转化为二元一次方程组的计算问题，解题思路流畅清新.

问题拓展

在数学学习中，普遍存在着运动变化、相互联系、相互转化的问题，这些问题中蕴含着丰富的辩证法的哲学观点，这些观点对于促进学生数学思维的发展和理性精神的树立具有重要的教育价值. 在本题中，运动变化和相互联系等观点同样表现得非常充分.

事实上，在这些具有普世价值的思想观念的引领下，一方面，可以指导我们对问题进行推广和拓展;另一方面，问题拓展探究的过程又有助于我们更加准确地把握和深刻地领会内隐问题中的数学本质.

1. 运动变化思想——点E在直线AB上运动

（1）当点E运动到BA的延长线上时，如图12所示，依题有∠EHD=45°，连接DB，∠DBE=45°，所以∠EHD=∠DBE.

所以D，E，H，B四点共圆.

所以∠EBH=∠EDH=45°.

所以HB是∠CBP的平分线.

由题意，得∠1=∠2.