初中数学常见解题错误类型剖析

[摘  要] 研究者认为初中数学学生常见的错误类型有：概念模糊，无中生有增条件;忽略实际，百密一疏致遗憾;转化不清，当着不着乱阵法;丢三落四，厚此薄彼出错误.在初中数学教学中教师应深挖学生错误产生的根源，培养学生的纠错习惯，帮助学生杜绝同样的错误重复发生.

[关键词] 解题;错误类型;策略;数学思维

俗话说：“错误是通向成功的阶梯.”初中学生在学习中产生的错误不能简单地归因于学生的马虎、粗心等，教师在初中数学教学中应深挖学生错误产生的根源，因势利导，帮助学生杜绝同样的错误重复发生. 为此，笔者针对学生常见错误类型进行剖析，并采取一定的应对措施，取得了阶段性的成果.

概念模糊，无中生有增条件

有些学生因基础知识掌握得不够扎实，解题时浑浑噩噩，甚至会根据自己的解题需求，凭空捏造一些不符合实际的条件，以满足自己的自圆其说;也有部分学生选择直接忽略试题中的一些条件，进行解题;还有些学生看到试题，觉得似曾相识，在哪里做过，解题时纯粹凭借自己的直观感觉进行解题，对问题的本质置若罔闻.

出现这种现象的主要原因还在于学生对概念、定义或法则等的内涵不清晰，对数学事实没有一个精准的理解，在运用时则无法灵活运用. 这种对概念类学习似是而非的态度，不仅导致了解题失败，还会阻碍各项数学能力的发展.

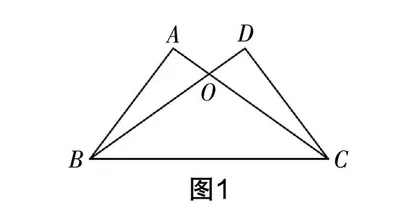
例1  如图1，已知∠ABC与∠BCD相等，试增添一个条件，让△BCA≌△CBD，并证明.

错解：添加AC=DB的条件.

错误证明：根据以下三个条件①∠ABC=∠BCD（已知）;②AC=DB（已知）;③BC=CB（公共边），可证明△BCA≌△CBD.

分析：从该条件的添加与证明过程来观察，学生是从“SSA”这个角度来证明两个三角形是全等的关系. 但是，在其判定定理中，并不存在“SSA”这一说法. 可见，学生是在对三角形全等的判定定理没有掌握的基础上进行解题，因而出现了上述错误.

正解：根据判定定理，本题可添加的条件有：①AB=DC;②∠A=∠D;③∠BCA=∠CBD. （证明过程略）

掌握概念、定理或法则等是数学学习的基本前提，是解题的基本保证. 学生一旦对概念的内涵或外延模糊不清，或无法精准把握概念之间的联系与适用范围，那么在解题时定会出现各种各样令人啼笑皆非的错误. 因此，教师在这些基础知识的教学中，应关注学生的理解程度，只有学生将这些内容真正地内化为自己的技能，才能做到解题时思路清晰，胸有成竹，避免因概念模糊而出现的错误.

忽略实际，百密一疏致遗憾

有些学生遇到冗长的文字题，心理上就产生抵触感. 读题审题时走马观花，甚至直接忽略试题的关键性词语或条件，在对题意尚未十分清晰的状态下就匆匆答题，从而导致错误的发生. 但也有部分学生不仅拥有良好的读题审题习惯，还具有缜密的思维与良好的辩证能力. 解题时，能做到条理清晰，思路明朗，却在最重要的环节，忽略了实际情况而造成遗憾.

例2  已知，等腰三角形ABC的两边长分别是2和5，求△ABC的周长.

学生看到本题，都觉得很简单. 经笔者统计，全班51人，本题完全答对的只有33人，还有的学生出现了两个答案，因此本题的正确率仅有64.7%.

错解：等腰三角形的两边分别为2和5，周长分别为：①2+2+5=9;②5+5+2=12，所以△ABC的周长是9或12.

分析：根据边长求三角形的周长，对学生来说没有什么障碍. 但是，出现错误的学生缺乏细致的思考，在三角形的性质中就提到：两边之和必须大于第三条边. 若以2为△ABC的腰，两条腰的和为4，而第三条边的边长为5，因为4<5，所以以2为腰，无法构成一个三角形. 因此，本题的解只能是12.

解题不仅需要扎实的基础知识与技能，还需要有细致的分析能力. 当遇到一些不确定的条件或因素时，不仅要分类归纳出所有存在的可能性，还要慎重思考其获得的结论与问题的性质、定理或事实是否相符. 只有及时排除不可能存在的情况，才能获得准确的答案.

<D：＼数学教学通讯中旬＼2022数学教学通讯中旬（08期）＼2022数学教学通讯中旬（05期） c＼aa-2.tif> 转化不清，当着不着乱阵法

有些学生解题并没有障碍，一旦遇到运算符号的转化问题，会屡做屡错. 尤其在一元一次不等式的运算中，不等号转化的错误发生率相当高. 为此，笔者特地访谈了部分常做常错的学生，他们的问题主要在于对转化的规则不清晰，即使能用语言表达转化规则，但在实际运算时，一不小心就乱了阵法.

例3  解不等式1-y>7y-3.

此题看似简单，但实际错误率并不低.

错解：通过移项可得-y-7y>1+3，合并同类项得-8y>4，在方程的两边同时“÷（-8）”，解得y>-.

分析：在解不等式的过程中，不仅移项这个环节需要注意变号，在不等式的两边同时乘或除以一个负数时，也需要变号. 从以上解题过程来看，存在着以下几个问题：①在移项这个环节，不等号右边的-3并没有移项，因此不应该变化它的符号;②不等号左边的1，移到不等号的右侧，需要变号;③当方程的两边都“÷（-8）”时，也应该变号. 因此，以上解题过程存在着明显的当着不着的问题.

正解：通过移项可得-y-7y>-3-1，得-8y>-4，两边同时“÷（-8）”可得y<.

符号转化是运算中常遇到的问题，若搞不清楚规则，则无法正确运算. 因此，教学时教师应针对性地进行强化训练，引导学生关注什么情况下需要转化符号，什么情况下不需要转化符号，并通过对比与实践训练逐步增强学生的认识，强化理解.

认知心理学提出：知识的内化过程受个体原有认知结构与先天倾向的影响. 学生对运算符号转化问题的障碍，与他们原有认知结构与思维定式有着很大的关系. 因此，教师应设法建构学生大脑中对运算的原有认知与新知的联系，深化学生对符号变化的掌握与理解程度，以提高他们的运算能力.

丢三落四，厚此薄彼出错误

纵观学生经历过的大小考试，都存在着因丢三落四的问题而导致的失分，甚至有学生出现漏题的现象. 有人认为出现这样的问题是因为学生马虎、不细致，其实从丢三落四的习惯能看出学生对待试题的态度缺乏严谨性. 想让学生突破这种障碍，教师可在课堂中勤加训练，让学生逐渐养成集中注意力、严谨、规范的解题习惯.

如学生在解一元一次不等式或方程时，为了将不等式或方程转化为整数，解题时存在着去分母的环节. 笔者发现，在不等式或方程的两边同时乘以各分母的最小公倍数时，很多学生会因为厚此薄彼而出现丢三落四的错误.

例4  解方程 =2-.

此方程比较简单，分母的公倍数较小. 按照常理，学生应不存在什么解题障碍. 本题属于分层作业中的基础题，要求所有学生都必须掌握. 但是，笔者发现学生的作业中，在此题出现错误的学生还不在少数.

错解：将原式去分母，可得5（a-1）=2-2（a+2），去括号可得5a-5=2-2a-4，通过移项与合并同类项的步骤，解得7a=3，a=.

分析：出现以上错误的原因在于只将含有分母的项，乘以各分母的最小公倍数，忽视了不含分母的项. 事实上，去分母时需将方程两边的每一项都乘以10（最小公倍数），包括不含分母的项（2也要乘以10），如此才能确保去分母后所得到的式子与原式相等.

正解：去分母可得5（a-1）=20-2（a+2），去括号5a-5=20-2a-4，通过移项与合并同类项后解得7a=21，a=3.

此类错误在学生的作业或试卷中屡见不鲜. 为了帮助学生扫除障碍，除了要求学生掌握正确的解题规则之外，教师还要注重强化学生在此方面的训练，让学生在重点突出的训练、纠错中，逐渐形成耐心、严谨的解题习惯.

常见的错误类型也可从知识、方法、逻辑、心理等角度去剖析，但不论哪种类型的错误，都离不开纠错习惯的培养与技能的训练，尤其是丢三落四的错误则可通过严谨解题态度得以纠正. 因此，在课堂教学中要时刻提醒学生端正学习态度，规范解题方法，从细节着手，做到及时发现并解决问题，帮助学生养成良好的解题习惯，为其形成良好的数学思维品质奠定基础.