“以生为本”的初中数学课堂构建

［摘  要］ “以生为本”是新时期教育教学的新理念，是新课程改革的出发点和落脚点，是学生学习和发展的需要. “以生为本”就是从学生角度出发，发挥学生的主动性，让学生成为课堂的主人，为学生的综合发展打下坚实的基础. 文章以初中数学课堂教学为例，对初中数学教学中“以生为本”课堂构建的主要途径加以分析和研究，以期对教学实践起到一定的帮助作用.

［关键词］ 数学课堂；“以生为本”；构建策略

在传统的初中数学教学中，教师更多地关注学生基础知识的掌握、应试技巧的传授，忽视了学生学习兴趣的激发、综合能力的提升. 教师教得辛苦，学生学得乏味，教学效率低下. 爱因斯坦提出“兴趣是最好的老师”，杨振宁指出“兴趣是成功的秘诀”. 兴趣可以将学生的追求和爱好激发出来，促使其产生强烈的学习动机，从而积极、主动地参与到学习中，变“苦学”为“乐学”，构建自主乐学的课堂氛围. “以生为本”的数学教学，就是为学生营造乐学氛围，激发学生的情感和兴趣，促使他们自主学习，从而提升他们的课堂参与度，提升课堂教学效率. 下面，笔者就“以生为本”的初中数学课堂构建，结合教学实践，谈几点粗浅的认识，以飨读者.

找准学生求知的兴趣点，激发学生的参与兴趣

兴趣是学生学习的动力. 为此，构建“以生为本”的初中数学课堂的前提是激发学生的学习兴趣. 要激起学生浓厚的学习兴趣，就需要教师找到学生的兴趣点，从学生的兴趣点出发，创新教学方式，激发学生的学习兴趣，促使他们走进数学课堂，为构建自主学习、合作探究的有效课堂奠定基础.

以九年级“一元二次方程”的教学为例，教师应从一元二次方程在生活中的应用出发，找到学生感兴趣的地方，并在这个兴趣点上巧妙创设学生熟悉的生活情境，以激发学生的兴趣，调动学生学习的积极性，诱发学生探究的主动性. 为此，笔者提出了3个一元二次方程在实际生活中的运用实例，并在解决这些问题的过程中引领学生观察、分析与总结. 笔者提出的三个问题如下：

（1）一个正方形花园的面积是16 m2，那这个正方形花园的边长是多少米？

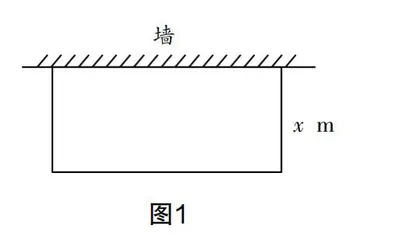
（2）如图1所示，一个长方形花圃一面靠墙，其他三边的长度之和为19 m，花圃的面积为24 m2，求花圃的长和宽.

（3）如图2所示，长为5 m的梯子斜靠在墙上，梯子底端与墙的距离是3 m. 如果梯子向右滑动的距离和梯子向下滑动的长度相等，均为x m，求x的值.

上述三个问题与学生的生活密切相关，因此，无论是问题的提出，还是问题的求解，对学生来说难度都不大，这容易激发他们学习的兴趣，能够增强他们学习的自信. 读懂题意列出3个方程后，笔者让学生分析这3个方程的特点，引导他们概括出“一元二次方程”的概念，从而将他们引入课堂知识的探究学习氛围.

再如，以九年级“圆与圆的位置关系”的教学为例，考虑到该部分知识较为抽象，而学生对动画感兴趣，所以笔者先借助多媒体的动态展示优势，为学生形象地呈现了两个圆位置关系的变动过程，让他们在观看动画的过程中，通过观察、分析、归纳，得出两个圆每一种位置关系的交点个数，及圆心距与两圆半径之间的关系；接着，笔者举出实例——用PPT展示奥运五环，让学生分别找出各圆环之间的位置关系……在多媒体动态、直观的演示之下，数学知识变得生动、形象，既能吸引学生的注意力，又能调动学生的积极性，这对激发学生的学习兴趣、培养学生的自主探究意识起着重要的作用.

找准知识学习的探究点，激发学生的探究热情

数学是一门应用学科，学生要学好数学就要培养自身的探究能力，这是由学科特点决定的，也是由学生独立人格的形成、创新学习意识的培养决定的，不仅如此，其还是新课改背景下、素质教育培养下新的人才培养观的基本出发点和终极目的. 这就要求教师在教学初中数学时，要找准知识的探究点，巧妙创设问题情境，将学生置于情境中，以发挥学生的课堂主体性，让学生在分析、解决问题的过程中，培养自主思考问题的习惯，不断激发探究学习的热情，凸显主体地位.

以八年级“全等三角形”的教学为例，要构建“以生为本”的课堂，教师就要改变传统“一言堂”的教学模式，要“让学于生”，将知识的构建权、课堂的主动权交给学生，让学生自主学习、主动探究. 为了提升学生自主探究的积极性、有效性，教师应根据教学重点、难点巧妙设计探究性学习任务，让学生明确该做什么、怎么做. 如“全等三角形”的教学重点是全等三角形的性质与运用，以及了解图形变化时识别三角形全等的方法，这也是教学活动的“探究点”，所以教师应围绕这些探究点设计探究性学习任务和活动，以任务和活动为载体，引领学生自主思考、合作探究.

如笔者教学时先呈现了如图3所示的信封，让学生仔细观察后思考：这个信封上盖着两个纪念邮戳，你们能说说这两个邮戳有哪些共同点吗？这两个邮戳能完全重合吗？你们的判断依据是什么？学生充分探究、交流后，得出了“全等三角形”的概念. 接着，笔者让学生画一个三角形ABC并剪下来，再剪一个与三角形ABC大小相等、形状相同的三角形DEF，将这两个三角形重合，再让学生找出它们的对应点、对应边、对应角……上述过程，学生在问题、任务的引领下，自主构建知识，课堂模式发生了根本性的变化，学生不再被动接受知识，而是自主参与活动、主动探究知识，使自身的主观能动性得到了充分发挥. 此外，如果在开展探究活动的过程中融入竞赛性质的游戏，如比一比谁最先发现三角形全等的性质等，则可以增加课堂的趣味性，更能激发学生的探究热情，课堂效率也会大幅度提升.

找准思维训练的切入点，诱发学生的思维欲望

数学学科的思维性、逻辑性均较强，培养学生的思维能力是数学教学的主要任务之一. 学生数学思维能力的高低决定了其解题能力的强弱. 但是，在传统的教学中，大多数教师忽视了学生思维能力的培养，采用灌输模式，剥夺了学生思维的权利和机会，使学生对所学知识不加咀嚼，囫囵吞枣，久而久之，没有养成自主思考的习惯，思维品质的培养也受到了制约. 而核心素养下的数学教学倡导“让学于生”，倡导“以生为本”，这就要求教师在数学教学中要找准思维训练的切入点，再在这个切入点上巧妙地提出问题，以激发学生的思维热情，调动他们主动学习的欲望.

以八年级“探索三角形全等的条件”的教学为例，在学生初步感知了“满足‘ASA’的条件，两个三角形便全等”之后，教师一般会给出一到两个例子，让学生对这个结论加以验证. 其中，给出例题之后，引导学生分析已知条件和求证的结果，找到求证的方法，写出求证过程等，都是对学生进行思维训练的切入点，在这个过程中，教师可通过提问，为学生打开思维之门. 如对于教材中的例题“已知△ABC≌△A′B′C′，AD是△ABC中BC边上的高，A′D′是△A′B′C′中B′C′边上的高，求证：AD=A′D′”，教师应停下讲解的步伐，在方法上给予学生问题性的引领，给学生“思”“探”的机会，从而培养他们的解题能力和思维能力. 比如笔者设计了如下问题引领学生深入思考：（1）要证明AD=A′D′，可以把AD和A′D′分别放在哪个三角形中？（2）只要证明这两个三角形怎样就行了？（3）这两个三角形全等吗？（4）哪些条件能说明这两个三角形全等？问题串的设计，能逐步引导学生思考，能培养学生良好的发散思维习惯和分析问题的能力，能让学生成为课堂的主人，成为会学习、会思考的学习者.

总之，“以生为本”的课堂是学生勤于思考、乐于探究的乐学课堂，是学生学习与发展的大舞台，师生分别扮演着导演和演员的角色. 第斯多惠指出，教育的艺术不在于传授知识，而在于唤醒、激励和鼓舞. 在这些先进教育理念的指引下，初中数学教师应从学生的学习特点出发，抓住学生的兴趣点、知识的探究点、思维训练的切入点等，巧妙设计任务和活动，将学生引领到课堂活动中，发挥学生的主观能动性，优化课堂模式，为学生的全面发展做好保障，从而实现学习质量的显著提升.