减中有增，增中求升

［摘  要］ 2021年，中共中央办公厅、国务院办公厅印发了《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》（以下简称“双减”政策）. “双减”政策的落地，给负担沉重的中小学生带来了福音，改善了他们课余时间被作业淹没的现状. 减少作业负担，实则呼吁减少中小学生花费在繁重作业上的“无用功”，而减轻校外培训负担的背后是对“教育面前人人平等”理念的回归. 文章基于“双减”政策探讨了初中数学作业如何布置.

［关键词］ 双减；作业设计；思考；价值

教师作为“双减”政策的执行者，承担着传播思想及践行政策的责任和义务. 在实施的过程中，笔者思考最多的就是：“双减”政策下教师如何布置作业？习题作为数学的重要组成部分，教师如何对习题进行取舍？减少作业量对学生的学习效果是否会有负面影响？对此，笔者进行了深入思考，在不断地学习专家对“双减”政策的解读及结合自身的教学实践反复斟酌后，越来越深刻地认识到，“双减”促使教师成长、促使教师改变，减轻作业负担实则是呼吁教师提高作业效率、改进练习价值、提升教学成效. 笔者以“双减”为指导，在教学实践中边尝试、边反思、边改进，就“双减”政策下如何减少作业量、提升作业价值谈几点不成熟的个人看法，权当是抛砖引玉.

“减”：严格控制习题数量

众所周知，“双减”政策围绕“减”而展开，对于初中数学而言，减少习题的数量无疑是对学生作业负担最直接的减轻. 所以，笔者在对习题课的预设中，不盲目追求课堂容量及练习强度，严格控制习题的数量，一切以知识的自然生长为出发点，让学生主动学习.

以八年级下册第六章“一次函数（习题课）”（苏科版，下同）的预设为例，可以编制如下习题：

1. 把一次函数y=2x-1的图像沿x轴向右平移1个单位长度，再向下平移3个单位长度，所得图像对应的函数表达式为______.

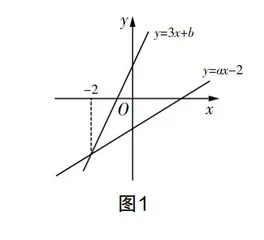
2. 如图1，已知直线y=3x+b与y=ax-2的交点的横坐标为-2，

（1）则关于x的方程3x+b=ax-2的解为______，

（2）则关于x的不等式3x+b≤ax-2的解集为______，

（3）则关于x的不等式3x+b>ax-2的解集为______.

3. 已知一次函数y=kx+b的图像经过点A（-1，-1）和点B（1，-3），求：

（1）一次函数的表达式；

（2）求直线AB与坐标轴围成的三角形的面积；

（3）请在x轴上找到一点P，使得PA+PB最小，并求出点P的坐标.

4. 如图2，已知函数y=x+1的图像与y轴交于点A，一次函数y=kx+b的图像经过点B（0，-1），与x轴以及y=x+1的图像分别交于点C，D，且点D的坐标为（1，n）.

（1）则n=________，k=________，b=________.

（2）求四边形AOCD的面积.

（3）在x轴上是否存在点P，使得以点P，C，D为顶点的三角形是直角三角形？若存在求出点P的坐标；若不存在，请说明理由.

设计意图  上述问题作为习题课师生共同探究的全部内容，相对“双减”之前的课堂容量来说有了大幅缩减，但是辐射面并没有缩小，问题中涉及的知识点包括一次函数的定义、性质、图像，一次函数与方程及不等式（组）的关系，一次函数与几何图形、最值问题等，基本涵盖了本章全部基础知识. 一次函数是初中数学三大函数中最简单的函数类型，“入门”是学习一次函数最重要的目标. 教学该部分内容时教师不要盲目追求习题的数量，而要将关注点置于学生的兴趣上. 习题数量的减少可以给学生提供深入思考及内化的时间，对学生思维的发展有着积极的作用.

“增”：全力提高习题质量

减量不减质是“双减”的正确打开方式，减轻学习的负担并非降低对学习效果的要求，因此减少习题数量的同时势必要提高习题的质量. 高质量的习题不仅能够有效激发学生的思维，调动学生的学习积极性，而且还能较大程度地减少学生的重复劳动，让每个问题都有它的价值，变“多练”为“精练”，体现双减的实质.

以八年级下册“平行四边形”的新授课为例，选定如下习题进行随堂训练：

1. 在平行四边形ABCD中，∠A比∠D大50°，则∠C=______°.

2. 若平行四边形ABCD的周长为40，AB=BC，则BC的长为______.

3. 如图3，平行四边形ABCD的顶点A，B，C的坐标分别是（0，1），（-2，-2），（2，-2），则顶点D的坐标是（      ）

A. （-4，1）    B. （4，-2）

C. （4，1）       D. （2，1）

4. 如图4：已知△ABC是等腰三角形，AB=AC，P是边BC上的一点，PE∥BA，PF∥CA，点E，F分别在AC，AB上，求证：PE+PF=AB.

设计意图  在平行四边形的第一课时教学中，教学目标是探究平行四边形的性质及尝试运用平行四边形的性质解决线段长度与角的度数问题. 对于新授课来说，试题难度要适中，既能巩固所学知识，又有一定的挑战性及探究价值. 上述问题中，题1与题2即为基本知识的巩固，其中包含了对平行四边形性质的直接运用，做法中渗透了方程思想；题3是将平行四边形置于平面直角坐标系中，让学生明晰平行四边形性质的同时为数形结合解决几何问题做好铺垫；题4稍有难度，由基础题往中档题过渡可以让学生在思维上有自然的进阶.

“找”：灵活把控训练时机

“双减”的实施呼吁还原学习的快乐本质，“寒窗苦读”不属于现代学生的学习特征. 减轻学生不必要的作业负担就是避免学科教学进行大量的、碎片化的机械训练，而以解决问题为主的数学学科，作业是不可或缺的，“双减”可促使教师去找寻两者之间的平衡，让教学质量和作业质量均能得到提高. 对此，笔者尝试了“见机行事”，灵活把控训练时机，在保证了习题数量和质量的前提下找到适切的时机让学生进行练习，将繁重的作业分散渗透在学习的各个时段.

如在教学完八年级上册“勾股定理”之后，针对学生作业及练习中错误率较高的题目进行二次练习：

1. 如图5，一只蚂蚁从长为7 cm、宽为5 cm、高为9 cm的长方体纸箱的A点沿纸箱爬到B点，那么它所走的最短路线的长是______cm.

2. 若等腰三角形的两边分别为12和10，则等腰三角形底边上的高为______.

3. 如图6，矩形ABCD中，AB=8，BC=4，将矩形沿AC折叠，点D落在点D′处，则重叠部分△AFC的面积为______.

4. 如图7，在△ABC中，∠C=90°，AC=4 cm，BC=3 cm，点E在AC上，现将△BCE沿BE翻折，使点C落在点C′处，连接AC′，则AC′长度的最小值是（      ）

A. 0.5 cm     B. 1 cm

C. 2 cm        D. 2.5 cm

5. 如图8，在△ABC中，AC=13，BC=20，AB=11，求△ABC的面积.

6. 已知：如图9，在Rt△ABC中，∠C=90°，AB=5 cm，AC=3 cm，动点P从点B出发沿射线BC 以1 cm/s的速度移动，设运动的时间为t秒.

（1）求BC边的长；

（2）当△ABP为直角三角形时，求t的值；

（3）当△ABP为等腰三角形时，求t的值.

设计意图  上述习题包含了路径最短问题、折叠问题、面积问题、动态问题等学生易错的知识. 题量不多，但是在单元学习结束以后进行有针对性训练的效果却较为显著，它可以让学生达到强化知识的目的，并且避免了大量不必要的重复练习. 除此之外，新授课中对当堂所学内容进行随堂练习、几何学习中对专题进行练习等都可以找准时机渗透在学习中，既能减轻学生的作业负担，又能提升学生的练习效果.

“改”：反思改进训练形式

作业是对学生所学知识的运用及所掌握技能的呈现，因此完成作业应该是学生能够主动执行且乐于接受的. 但由于过去作业量的超负荷使其失去了本真，学生闻之色变，作业的意义也就偏离了实际. “双减”呼吁减少作业量，还原做作业的快乐本质. 教师可以给予学生多种作业形式，让他们体会到做作业的乐趣，学会知识，掌握技能.

在实践中，笔者常常在单元复习课后布置“大家来找茬”的作业，具体做法是针对学生在学习中的易错题，把题目和错误答案全部呈现出来，让他们去纠错改错. 以下是八年级下册第10章“分式”习题课作业的一部分：

1. 已知关于x的分式方程-2=的解为非负数，则m的取值范围是m≥-2 .

2. 如果关于x的分式方程+=无解，则k的取值是 5或-.

设计意图  上述习题中，题1错在忽略分式有解的前提条件，题2错在对化简后的整式方程是否有意义缺乏思考，题3错在混淆了分式运算与分式方程中对分母的处理，题4错在对分式有意义的条件缺乏思考. 错误均出自学生本身，用纠错替代反复练习，在减轻学生作业负担的同时可以更精准地定位练习的目的，让学生有效避免类似错误的发生. 除此之外，实践作业、数学实验、数学游戏等均可以作为作业的形式，以此增强作业的吸引力. 多样化作业形式的实质在于减量不减质，提高作业的效率.

“双减”是国家基于新时代教育发展全局所做出的重大决策，减轻学生作业负担及课外培训负担的实质是让基础教育回归学校、让课程学习回归课堂，归还学生应有的学习时间，给予学生自我发展的空间. 对于学校教育而言，缩减学生的作业总量和作业时长的背后是对教学质量的更高要求. 作业量的减少要以作业质量的提升为保障，教学质量的提高要以学生的主动性为前提，这两者之间的平衡就在于教师如何去践行“双减”. “双减”背景下的教师一定是高水平、高素养的，这样才能培养出适应个人终身发展及社会发展需要的高素质学生，不断提升自身的素养不仅是当下教师的责任，还是教师整个生涯中的使命.

经过一段时期的学习及思考，笔者认为“减”数量、“增”质量、“升”素养是践行“双减”的总体目标及方向. 课堂教学肩负着提升学生学习质量及教师教学质量的重任，作业承载着学生学习进步及身心成长的职责，它的作用不可小觑，“减”中有“增”，“增”中求“升”，方能体现“双减”的实质，还学校教育一片蓝天，让教师和学生在知识中自由翱翔、共同进步.