高中数学不同版本教材数列概念内容的比较研究

［摘  要］ 数列概念是高中数学的重要概念. 研究者从编排思路与知识结构、概念形成的素材、用函数观点看数列、教材例题等角度入手，对人教A版（2019版）、苏教版（2021版）、北师大版（2019版）数学教材中的数列概念内容进行比较研究，并提出两个课时的教学建议.

［关键词］ 数列概念；教材比较；知识结构；函数观点

以《普通高中数学课程标准（2017年版）》（简称课程标准）为依据编写的新教材是新课程理念的集中体现，是数学学科核心素养在教学中落地的媒介. 不同版本的教材都严格按照课程标准进行编写，但具体内容的呈现方式和内容所折射出来的能力和素养要求又有一定差异. 因此，对不同版本的教材进行比较研究，能在领会教材的编写意图，吸取各版本教材的闪光点的基础上，创造性地使用教材.

数列是“函数”主题的内容之一，数列的学习是对函数的认识的深化.数列概念是高中数学的重要概念，是学生体会数学对象的获得过程和数学对象的研究思路的典型载体，其学习有助于培养学生的数学抽象素养.因此，有必要以教材为基础对数列概念进行深度研究.本文对人教A版（2019版）、苏教版（2021版）、北师大版（2019版）数学教材（分别简称人教A版教材、苏教版教材、北师大版教材）中的数列概念内容进行比较研究，并提出两个课时的教学建议.

三版本教材的比较

1. 编排思路与知识结构的比较

三版本教材的编排思路和重点内容大致相同——都按照如下思路编排内容：数列事实（实际例子）→抽象出数列的概念→概念辨析（数列是特殊函数）→数列的表示与性质. 它们都采用概念形成的方式建构数列的概念，即从典型丰富的具体案例中抽象出它们的共同特征，进而对数列下定义. 数列概念的抽象、数列通项公式的探究是三版本教材共同的重点内容. 从函数的视角看数列在三版本教材中都有重点体现.

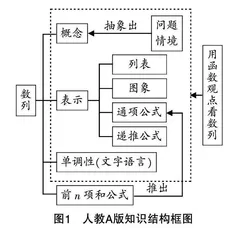
虽然三版本教材的编写总体思路相同，但知识结构有一定差异. （1）关于数列的表示，人教A版和苏教版教材给出的是列表、图象、通项公式、递推公式等四种方法，并以例题的形式呈现这四种表示方法，而北师大版教材没有用递推公式表示数列. （2）北师大版教材更加凸显用函数的观点看数列，将“数列的函数特性”单独作为一小节内容，并将研究函数的两条基本思路（形的角度直观认识和数的角度精确刻画）迁移到数列的研究中. （3）人教A版和北师大版教材都研究了数列的单调性，其中北师大版教材用文字语言、符号语言和图形语言等刻画数列的单调性，并且利用例题深化学生的理解，而人教A版教材仅用文字语言进行了刻画. 苏教版教材没有讲解数列的单调性. （4）人教A版教材介绍了数列的前n项和S，并说明通项a与S之间的关系，另外两版教材没有这部分内容. 三版本教材的知识结构图分别如图1、图2、图3所示.

2. 概念形成素材的比较

为了形成数列概念，三版本教材都用实例作为问题情境. 按照各版本教材实例的编排顺序分别编号，从实例的数量、来源、剖析、数列特征，以及与后续内容之间的联系等维度进行比较分析，整理成表1.

从表1可以看出，三版本教材的实例都能做到“低起点、高立意”. 首先，所选实例主要来自现实生活和熟悉的数学问题，便于学生理解. 其次，实例能揭示数列的本质特征. 实例所蕴含的数列既包含有规律的数列（如等差数列、等比数列），又包含没有规律的数列，避免学生误以为具有规律的一列数才是数列；数列的项既有整数，又有非整数，避免学生误认为数列的项只能是整数. 对学生可能出现的错误认识的规避意在指向数列的本质特征：数列是一列数，且这列数具有实际意义，不能调换顺序. 再次，实例成为推动数学知识发展的内在力量. 实例的共同特征让数列的概念呼之欲出，实例中的无穷数列让数列的通项公式和递推公式这两种表示方法的呈现成为必然.

人教A版对数列本质特征的揭示更充分，易于学生突破学习难点.在给出实例之前，用一句引导语“在现实生活和数学学习中，我们经常需要根据问题的意义，通过对一些数据按特定顺序排列的方法来刻画研究对象”呈现本节内容的先行组织者.引导语中的“一些数据”和“特定顺序”顺应学生的学习心理，具有统摄性，指明三个实例的分析方向. 然后以“示范+模仿”的方式帮助学生了解数列，如通过第一实例和第二实例的详细分析，引导学生体会数列中的数不能交换位置，在此基础上指出它们都是“具有确定顺序的一列数”. 接着在第三实例后面提出问题引发学生思考：“你能仿造上面的叙述，说明第三实例中的数也是具有确定顺序的一列数吗？”最后引导学生归纳三个实例的共同特征. 由于学生难以从实例中直接提炼数列的本质特征——具有确定顺序的一列数，因此教材搭建思维台阶，聚焦思考方向，便于学生抽象概念.

苏教版和北师大版教材给学生提供了更多自主探究的空间.它们给出实例前，没有针对实例提出思考方向，而是呈现更丰富的例子（苏教版6个，北师大版5个），进而帮助学生从众多实例中抽象概括出“一定次序排列的一列数”. 学生没有受到问题起源阐述的思考限制，可以从不同角度进行分析、归纳、提炼，在充分体验概念形成的过程中，逐步增强问题意识，发展数学抽象素养. 同时，苏教版教材注重内容的前后联系，实例1与实例2和实例3与实例4分别在等差数列和等比数列的定义中作为问题情境素材再次被利用.

3. 用函数观点看数列的比较

课程标准指出“了解数列是一种特殊的函数”，并要求“感受数列与函数的共性与差异，体会数学的整体性”.三版本教材都从三个角度让学生体会数列是特殊的函数：第一，数列满足函数的定义.数列中每一个给定的序号n，都有唯一的项a与之对应，符合函数的定义. 为帮助学生理解，三版本教材都用表格直观呈现这种对应关系. 第二，用函数的三种表示方法来表示数列. 函数有列表法、图象法、解析式法三种表示方法，分别对应数列的列表法、图象法、通项公式法. 第三，数列是特殊的函数，其特殊性在于定义域为正整数集或其有限子集，因此数列的图象是一些孤立的点.

三版本教材在内容组织、侧重点、语言的描述上有一定差异. 首先，用表格呈现序号n与项a的对应关系时，呈现形式和顺序不全相同. 北师大版教材先以具体数列a=为例，再过渡到一般数列，分别分析序号n与项a的对应关系；人教A版教材先介绍一般数列的序号n与项a的对应关系，再用表格和图象来表示具体数列的序号n与项a的对应关系；苏教版教材以文字语言直接指出数列是特殊的函数，在例题（例2）中用表格引导学生进一步认识序号n与项a的对应关系. 其次，北师大版教材没有局限于从定义和表示方法挖掘数列与函数的内在联系，而是更注重研究方法的渗透. 它以数列的单调性为载体，引导学生将函数单调性的研究方法中的作差法和图象分析法迁移到数列中，让学生深刻体会用函数的观点看数列，用函数的研究方法研究数列. 再次，行文风格上，苏教版教材更“隐晦”，人教A版和北师大版教材更“直接”. 例如，“数列的通项公式就是相应函数的解析式”在人教A版和北师大版教材都有，人教A版更是指出“与其他函数一样，数列也可以用表格和图象来表示”，这些文字都清晰直接地说明了数列与函数在表示方法上的一致性. 苏教版教材则含蓄地描述为“数列可以由通项公式来给定，也可以通过列表或图象来表示”，这样表达给了学生思考和联想的空间.

4. 教材例题的比较

人教A版、苏教版、北师大版教材中的例题分别有5个、4个、5个，按照各版本教材例题的编排顺序分别编号，得到三版本教材例题内容一览表（如表2所示）. 从设计意图来看，人教A版和苏教版中的例题以知识立意为主，以能力和素养立意为辅. 两版本教材主要围绕通项公式和递推公式设置例题.根据通项公式写出前几项并作图象，以及根据递推公式写出前几项，都是对数列概念的理解和表示方法的应用；根据通项公式判断某个数是否为数列中的项，意在将求数列中的项数n转化为求方程的正整数解. 这些例题相对简单，学生容易理解，可以帮助学生巩固和运用本章节的主要知识，培养学生的计算能力和理性精神. 根据数列的前几项写出它的一个通项公式对学生来说有一定难度，需要通过观察、计算，寻找项数n与通项a的对应关系，并用数学符号表达出来，可以发展学生的逻辑推理素养.

北师大版教材中的例题侧重能力和素养立意，兼顾知识立意. 主要围绕通项公式和单调性设置例题，并有一个例题是数列的表示方法与单调性相结合的实际应用问题.北师大版教材中的例题与人教A版和苏教版教材中的例题的最大不同在于其通过数列的通项公式（或通项）研究数列的单调性，需要学生先了解数列单调性的符号化表达，再调用已有的学习经验，将函数单调性的判断方法迁移到数列中，不仅能帮助学生理解数列的本质，促进知识内化，还能在与函数的研究方法的联系中帮助学生建构方法体系，提升数学方法的迁移能力. 北师大版教材中的实际应用问题有一定难度，需要学生通过文字阅读，提取信息，并用符号和图象表示，有助于学生阅读理解能力、推理能力和数学建模能力的提升.

综上所述，三版本教材在落实新课程理念的基础上各具特色. 人教A版教材知识内容全面、脉络清晰，概念形成过程注重示范，突破学习难点，揭示数学本质，例题选择兼顾知识巩固与能力发展. 苏教版教材知识内容简明，突出主干知识，注重从单元整体架构的角度选择学习素材，以典型丰富的例子促进概念形成，例题选择精炼且基础. 北师大版教材强调数列与函数的联系，注重知识体系的构建和研究方法的迁移，例题选择对学生的数学能力有一定要求.

教学建议

基于上述三版本教材的比较分析，综合它们的优点进行教学.以数列的概念为载体，让学生明晰研究数学对象的基本路径，发展其认知结构，完善其认知体系.

因为递推公式反映了数列的项之间的迭代关系，是数列重要的表示形式；数列的前n项和S与通项a之间的关系是后续学习构造法证明数列型不等式的主要依据；数列的单调性对体会数列与函数之间的关系具有不可替代的作用. 因此，将递推公式、前n项和、单调性三部分内容都列入教学内容. 从内容上对“数列的概念”单元划分课时如下：

课时1：数列的概念（1）——数列概念的形成、数列概念的辨析、数列的三种表示.

课时2：数列的概念（2）——数列的递推公式、单调性、前n项和.

现呈现每个课时教学设计的重点环节.

1. 课时1：数列的概念（1）

师：高一时我们研究了重要的数学对象——函数.回顾函数的研究思路“现实情境→函数概念→符号表示→具体函数→知识应用”.本节课开始，我们将研究一种新的数学对象.

（1）问题情境，形成概念

情境1［1］ 王芳从1岁到17岁，每年生日那天测量身高. 将这些身高数据（单位：cm）依次排成一列数：

75，87，96，103，110，116，120，128， 138，145，153，158，160，162，163，165， 168. ①

情境2［1］ 在两河流域发掘的一块泥版上，有一列依次表示一个月中从第1天到第15天每天月亮可见部分的数：

5，10，20，40，80，96，112，128，144， 160，176，192，208，224，240. ②

情境3［1］ -的n次幂按1次幂、2次幂、3次幂、4次幂……依次排成一列数：

-，，-，，…. ③

情境4［2］ 某种树木第1年长出幼枝，第2年幼枝长成粗干，第3年粗干可生出幼枝（如图4所示），那么按照这个规律，各年树木的枝干数依次为：

1，1，2，3，5，8，….④

问题1 根据情境1和情境2，回答下列问题.

①情境1中，第4、第6个数的实际意义分别是什么？若交换103和116的顺序，所表示的实际意义还一样吗？

②如何表示每一个数所在的位置？能否引入一个符号，表示上述情境中的数？