关于分析法与综合法的教学指导探究

[摘  要] 分析法与综合法在数学解题中的应用极为广泛，掌握方法思路，以及背后的思维过程十分关键，也是教学重点. 研究者采用思维导图解读分析法与综合法，并结合实例开展应用探究，提出相应的教学建议.

[关键词] 分析法;综合法;思维;应用

方法解读

数学问题的解法众多，分析法和综合法是其中使用频次较高的方法，在不等式、方程、圆锥曲线等问题解决中有着广泛的应用. 合理使用有助于深度解析条件，从而高效构建解题策略. 在实际教学中，需要指导学生掌握分析法和综合法的构建思路.

1. 思维讲解

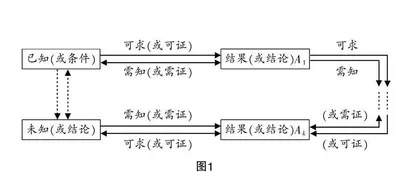
建议教学中呈现如图1所示的思维导图，其中内环为分析法的解析过程，外环为综合法的解析过程.

从整体视角来看，分析法的解析过程为“执果索因”，即从待验证的结论出发，逐步逆向探索其成立的条件，直至回溯到已知条件、定理及定义. 如图1所示，内环先假设结论成立或正确，随后逐步探索其成立的条件，将问题层层转化，最终构建起与已知（或条件）的紧密联系.

综合法的解析过程为“由因导果”，即“由原因来推导结果”，证明命题正确. 如图1所示，外环从已知（或条件）出发，结合定义和定理逐级推导，直至得到最终结论.

2. 特点讲解

在解题时，分析法与综合法既可独立施展，亦可相辅相成，共同构建知识框架. 对应的思想方法独具特色，教学中需着重引导学生深入理解，并明确以下三大要点.

（1）方法上互相依存、相互补充：使用综合法遇到思维障碍时，可采用分析法进行逆向分析和探究.

（2）过程中互相交替、相互转化：解析问题时可以相互切换分析法与综合法，辅助构建解题思路.

（3）结论在反向推导的过程中得以验证，即解题过程中的“条件”与“结论”，均可借助分析法与综合法进行有效的验证.

在教学中，建议将分析法作为解题探究的起始点，以此明确解题的切入点，随后采用综合法来构建和完善解题过程.

应用探究

分析法与综合法是解题的两大利器，教学中需引导学生灵活运用，掌握构建思路. 在“应用探究”阶段，建议采用分阶段、多角度的探究方式.

1. 多解探究

多解探究，即针对同一问题探究多种解法，指导学生分别运用分析法和综合法来解析问题. 教学中注意突出这两种方法的特点，并引导学生深入体会与领悟.

例1 已知a>0，b>0，且a+b=1，求证：

a+

b+

≥.

思路分析 证明不等式成立的方法众多，总体上可归纳为综合法与分析法两种. 分析法从结论出发，通过转化，探索其成立的条件;综合法则从已知条件出发，通过逻辑推理得出结论.

证法1（综合法） 利用综合法证明不等式成立，即采用正向顺推的策略，结合题目给定的条件，探索

a+

·

b+

的取值范围. 过程如下：先打开

a+

b+

的括号，得

a+

·

b+

=ab+++;然后拆解，得ab+++=ab++++;最后利用均值不等式得ab++++≥2+2+=. 证毕.

证法2（分析法） 利用分析法证明不等式成立，即采用反向逆推的策略，等价转化不等式

a+

b+

≥，构建与已知条件之间的关系. 过程如下：证明原不等式成立，即证明（a2+1）（b2+1）≥ab成立，即证明4（ab）2+4（a2+b2）-25ab+4≥0成立. 已知a+b=1，则a2+b2=（a+b）2-2ab=1-2ab. 将其代入上式，可得4（ab）2+4（1-2ab）-25ab+4≥0，即证明4（ab）2-33ab+8≥0成立. 解此不等式，可知需证明ab≤或ab≥8，而ab≥8显然不成立，故需证明ab≤. 已知a>0，b>0，且a+b=1≥2，可得ab≤. 因此，原不等式成立.

评析 综合法与分析法各具特色：综合法以其直观性便于表达，而分析法则擅长于深入剖析，促进思考. 两者在切入角度与推导逻辑上存在显著的差异. 在教学时，建议引领学生深入挖掘题设条件与问题之间的内在联系，并鼓励他们采用熟悉的解题策略进行推理. 在多解探究中，尤其要重视引导学生对比不同解法，进而总结各个解法的特点与优势.

2. 分层探究

综合性问题通常以分层设问的方式呈现，即设计多个子问题，需要逐一解析与探究. 在此过程中，灵活运用分析法或综合法可以有效达成目标. 具体而言，就是针对问题的各个小问，使用分析法或综合法来构建解析思路. 在教学中，教师应引导学生密切关注题设条件，并根据问题的具体情形灵活选用合适的方法.

例2 设函数f（x）=aexlnx+，曲线y=f（x）在点（1，f（1））处的切线为y=e（x-1）+2.

（1）试求a和b的值;

（2）证明：f（x）>1.

思路分析 本题是涉及函数、导数与不等式的综合性问题. 题设两问，第（1）问求的是参数的值，采用综合法来解答相对简单一些. 第（2）问以函数为背景构建不等式，其特点是条件复杂，而需要证明的结论却相对简明，建议采用分析法求解.

过程引导 （1）采用综合法求解参数的值.

函数f（x）的定义域为（0，+∞），对应的导函数f′（x）=aexlnx+-ex-1. 根据题意可得f（1）=2，f′（1）=e，求得a=1，b=2.

（2）采用分析法证明不等式.

由（1）问可知f（x）=exlnx+. 因此，证明f（x）>1，即证明exlnx+>1①. 将①式两边同时除以ex-1，即证明elnx+>②. 观察②式的结构，鉴于其含有3个完全不同的项，于是尝试将其转化为同一类别的表达形式.

当x>0时，ex>x+1，用x-1代替x，可得ex-1>x，即<. 因此，证明elnx+>，即证明elnx+≥0.

令g（x）=elnx+，则对应的导函数g′（x）=-=. 令g′（x）=0，可得x=. 分析可知：当x∈

0，

时，g′（x）<0，则g（x）在区间

0，

上单调递减;当x∈

，+∞

时，g′（x）>0，则g（x）在区间

，+∞

上单调递增. 因此，g（x）=g

=0，即elnx+≥0. 所以，原不等式成立.

评析 对于综合性问题，可采用分析法和综合法来分层破解. 第（1）问采用综合法进行解析，依据题目给定的条件逐步推导出参数的值. 而第（2）问则运用分析法进行剖析，通过等价转化，将不等式成立的问题转化为函数的最值问题，利用函数的性质完成证明.

3. 综合运用

分析法和综合法不仅可以独立使用，对于综合性极强的复杂问题，还可以将这两种方法结合起来运用，即使用分析法探寻解答思路，运用综合法构建解答过程.

例3 已知函数f（x）=log（x+2），a，b，c是两两不相等的正数，且a，b，c成等比数列，试判断f（a）+f（c）与2f（b）的大小关系，并证明结论.

思路分析 本题是一道分析题，涉及函数、等比数列等相关知识，求解时可采用“猜想—证明”的策略：先举特例猜想结论，再运用分析法给出求解思路，最后利用综合法构建证明过程.

过程引导 分两步求解：先举特例猜想结论，再分析证明猜想.

第一步，举特例猜想结论.

取a=1，b=2，c=4，则f（a）+f（c）=f（1）+f（4）=log23+log26=log218，2f（b）=2log24=log216. 由于log218>log216，故猜测f（a）+f（c）>2f（b）.

第二步，分析证明猜想.

证明f（a）+f（c）>2f（b），即证明log（a+2）+log（c+2）>2log（b+2），即证明log[（a+2）（c+2）]>log（b+2）2，即证明（a+2）（c+2）>（b+2）2.

分析可知（a+2）（c+2）>（b+2）2，函数f（x）=logx为增函数，所以log[（a+2）（c+2）]>log（b+2）2，即log（a+2）+log（c+2）>2log（b+2），故f（a）+f（c）>2f（b）.

评析 上述问题的解析过程总体上遵循了“猜想—验证”的逻辑框架，而在具体实施上，则是对分析法与综合法的综合运用. 教学中需引导学生精准把握分析法与综合法综合运用的核心思路，实现问题的巧妙转化，并深入探究其背后的条件，从而顺利解决问题.

教学反思

分析法与综合法是数学常用的解析方法，在解题时既可以单独使用，也可以综合使用. 下面结合教学实践提出几点教学建议.

1. 构建思维导图，直观辨析讲解

分析法与综合法是数学常用的解析方法，从字面上难以直观理解其含义，教学中建议构建思维导图，直观辨析讲解，使学生充分理解分析法的“执果索因”，以及综合法的“由因导果”. 在构建思维导图时，注意把握已知条件、推导条件，以及最终结论之间的关系，并结合实例来串联构建，充分讲解.

2. 实例应用讲解，全面呈现过程

研究分析法与综合法的应用是教学重点，需紧密围绕其三大应用策略，以构建解题框架. 具体而言，在“多解探究”环节，针对同一问题，引导学生分别采用分析法和综合法来探寻解答路径;在“分层探究”环节，针对同一问题，引导学生运用这两种方法逐一攻克各个小问题;而在“综合运用”环节，则引导学生巧妙平衡分析法与综合法的运用，探索创新解题思路，从而构建起完整而高效的解题流程.

3. 注意思路引导，培养数学思维

数学解题教学，应将重点放在思路方法的引导上，侧重于培养学生的数学思维. 关于数学思维的培养，建议从以下三个方面进行：首先，从思维角度深入剖析方法的运用过程，并进行详尽的解读与辨析;其次，紧密结合解题实践，引导学生进行方法运用的思维探索，适时设问以激发其思考潜能;最后，从思想层面切入，开展深入的教学反思，引导学生领悟方法背后所蕴含的数学思想.

写在最后

关于分析法与综合法的应用教学，建议结合思维导图，引导学生深刻理解方法的内涵，并通过实例应用，进一步指导学生构建清晰的解题思路，提升学生的思维能力.