基于学科德育的高中数学教学实践与思考

［摘  要］ 随着课改的不断深入，数学教育愈发强调其德育功能. 文章以“雪花曲线的探究”为例，分别从理性、人文、人格和责任四个维度分析数学学科德育内涵的具体呈现形式，并通过课堂各环节的德育渗透，发展学生的数学核心素养，有效实现数学学科的育人价值.

［关键词］ 学科德育；高中数学；雪花曲线；分形几何

党的十八大将立德树人作为教育根本任务以来，学科德育成为一线教师关注的热点，课堂教学成为落实该任务的基本形式. 《普通高中数学课程标准（2017年版2020年修订）》中明确指出：“数学教育承载着落实立德树人根本任务、发展素质教育的功能……在学生形成正确人生观、价值观、世界观等方面发挥独特作用.”［1］可见，高中数学课堂不仅承载着知识的传递功能，其学科德育对学生的润泽和渗透作用同样值得重视. 本文以一节“雪花曲线的探究”课为例，具体呈现学科德育在课堂教学中的蕴藏形式.

[⇩] 数学学科德育内涵

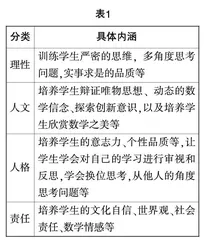
学科德育是指教师在日常学科教学过程中融合德育，以学科为抓手凸显育人价值. 而数学学科德育特指数学教师在数学教学中进行德育渗透，实现数学学科的育人价值. 有学者认为［2］，数学学科德育内涵主要有理性、人文、人格和责任四部分（见表1）.

[⇩] 数学学科德育教学实践

本文以“雪花曲线的探究”为例，将时事热点作为课程的引入情境，用数学文化构建例题背景，以课外阅读的方式采编史料，通过课堂实验、合作交流、汇报演讲等教学活动，设计有效的问题串和多元化的作业等方法，实现数学学科德育在课堂中的渗透，力求在教学各环节较为自然地埋设“德育点”，通过关注学生言行表现对课堂德育效果进行感知，通过理性、人文、人格和责任四部分对本节课的数学学科德育实践进行分析.

1. 教学分析

（1）教学内容分析

在《普通高中教科书数学选择性必修第一册（2020年沪教版）》第四章“数列”第二节等比数列中，教材以“科克雪花曲线”为例引入等比数列，章末复习又以求“雪花曲线”的周长和面积的拓展题形成首尾呼应，章节中还呈现了关于“谢尔宾斯基三角形”和“谢尔宾斯基正方形”的练习题. 沪教版二期课改教材曾专门将“雪花曲线”作为数列的章末拓展阅读. 新旧教材都把“雪花曲线”纳入其中，旨在通过学生对“雪花曲线”的探索与研究，培养他们应用数列知识解决实际问题的能力，同时也是对数学分支——分形几何的初探和引导. 本课将以“雪花曲线”的探究为明线，数列的综合应用为暗线，分形几何的介绍为延伸，揭示事物的本质规律，提升学生的数学素养，渗透数学的学科德育.

（2）学情分析

知识方面，学生已完成等差数列、等比数列的学习，会求解一般数列的通项公式，能初步应用数列知识解决一些问题；能力方面，高二学生有通过相互讨论去分析和解决问题的能力；情感方面，借助对雪花的感性认识，激发学生利用数列知识探究“雪花曲线”的兴趣.

（3）教学目标

①通过计算“雪花曲线”的周长和面积，巩固数列与极限的有关知识，体会从特殊到一般的数学思想方法，发展数学抽象、直观想象、逻辑推理、数学运算等素养.

②经历动手作图、合作研究的过程，培养学生提出问题、分析问题、解决问题，得出科学结论的数学探究能力.

③了解分形几何的历史与发展，欣赏分形艺术，让学生感悟数学的科学价值、应用价值、文化价值和审美价值.

（4）教学重难点

教学重点：对“雪花曲线”的周长无限大而面积有限的认识；了解分形几何.

教学难点：求解“雪花曲线”的周长与面积的通项公式.

（5）教学准备

①课堂学习单；

②安排学生志愿者提前搜索有关分形几何的资料，并交予教师修改、审核后制成PPT备用.

2. 教学过程

（1）环节1：创设情境，引出课题

情境1：

师：是否存在一种曲线，它的长度可以绕地球好几圈，却能画在一张小小的邮票上？答案如何，学习完本节课就可以揭晓！

情境2：

师：2022年北京冬奥会成功举办，成为全球上首个“双奥之城”. 在2月4日的开幕式上，一朵小小的雪花成为贯穿开幕式始终的线索，所有参赛国家和地区名字的雪花引导牌最后组成一个美丽的大雪花. 在全球处于疫情的艰难时刻，总导演张艺谋力图运用艺术感染力和文化共通性，体现人类团结，一起走向未来.

设计意图：情境1通过一个看似不可能发生的事情引发学生的认知冲突，情境2以近期发生的时事新闻调动学生的学习兴趣，并为探究“雪花曲线”埋下伏笔.

德育点：从理性维度来说，情境1启发学生打破思维定式，追求实事求是的品质；情境2呈现了2022年北京冬奥会开幕式视频，展现了震撼人心的美，从人文维度来说，赋予学生民族自豪感.

（2）环节2：手动作图，自主探索

师：小小的雪花到底蕴藏着多大的秘密，我们今天不妨来一探究竟！

1904年瑞典数学家科赫第一次用数学的方法描述了一种曲线，外形酷似一片雪花，所以我们称它为“雪花曲线”或“科赫曲线”. 下面我们也用数学的方法尝试制作一片“雪花”. 请同学们进行小组合作，在纸上完成以下操作：

第一步，将图2-①的正三角形的每边三等分，并以中间的一条线段为底边向形外作等边三角形，然后去掉底边，得到图②；

第二步，将图2-②的每边三等分，重复上述的作图方法，得到图2-③；

第三步，按上述方法无限多次继续做下去，得到的曲线将会呈什么形状？

设计意图：合理设计操作探究活动，可以有效调动学生的学习兴趣和参与的积极性.让学生带着对雪花的感性认识转而理性地研究“雪花曲线”，通过操作探究活动，获得宝贵的活动体验经验，培养学生数学抽象和直观想象的数学核心素养.

德育点：在高中数学教学中，受行为主义影响较深的传统教学观念长期存在，教学内容呈现出了相对固化的特征，这也就导致数学教学总体上比较枯燥乏味，教学效果也较为一般，学生一旦面对一些相对抽象的内容，基本上都会出现难以理解与掌握的现象［3］. 数学史的融入是数学教学体现人文性的有力抓手.从数学德育的责任维度来说，通过“雪花曲线”历史故事的引入，渗透多元文化，拓展学生的文化视野.

师：通过自己动手，大家都作出了“雪花曲线”. 但是我们发现，随着生长次数的增加，小三角形越来越多，作图也越来越困难.下面我们借助软件，看看把“雪花曲线”的局部不断放大后会是什么样子.

教师利用几何画板缩小一个曲线与另一个不变的曲线进行对比，让学生初步感受分形结构的自相似性，如图3所示.

设计意图：让学生动手作图，熟悉曲线的迭代作图法，对曲线的无限生长有一个初步印象；再利用计算机技术，增加迭代次数，让学生观察放缩后的“雪花曲线”，发现曲线局部间的相似特征，从而对曲线的自相似性有一个初步的“形”的认识.

德育点：有效探究活动的设计是促进学生主动思考的平台，学生先动手，再通过计算机进行多次迭代，从理性维度出发，鼓励学生运用已知的方法或结论类比未知的问题；从人格维度来说，哪怕学生在作图时遇到了困难，也能让他们在事物的曲折发展中认识挫折的价值.

（3）环节3：定量分析，合作研究

师：“雪花曲线”其实蕴藏着一些非常奇特的性质.刚才大家都体验了“雪花曲线”的生成过程，观察你们作出的图形，查看“雪花曲线”有什么特点.

生1：“雪花曲线”是一条连续的折线.

生2：曲线到处长满了“角”.

生3：当迭代次数越来越多时，“角”的个数也越来越多，并且“角”越来越小.

生4：曲线向外生长得越来越慢.

师：大家从“形”的方面对“雪花曲线”有了初步认识.接下来，我们不妨从“数”的方面来定量研究“雪花曲线”. 同学们觉得我们可以研究哪些方面？

生5：可以研究“雪花曲线”的边长和边数.

生6：还有“角”的个数.

生7：周长和面积.

师：非常好！同学们已经具备了用数学的眼光观察世界的能力.

设计意图：教师提出问题启发学生观察“雪花曲线”的形状，发现它是一个与我们平时研究的多边形不同的平面多边形，引导他们从边长、边数、周长、面积等方面提出问题.

德育点：从人格维度来说，通过师生问答，营造良好的课堂氛围，借助合作学习培养学生尊重他人的思想意识，结合教学内容布置合作学习任务，促使学生在合作完成学习任务的过程中，倾听他人意见，相互学习优点，并对比分析自身不足，逐渐提升自我.

师：方便起见，我们统一数据：设原正三角形的边长为a，周长为L，面积为S，不妨把每一次作图变化的过程叫做“生长”，则经过第n次生长后曲线的周长为L，面积为S.请同学们尝试填写表2.（文中展示的是已经填写好的表格）

设计意图：学生经历互相交流、合作探究的过程后归纳出曲线生长的一般规律，抽象成数列模型后求得通项公式，最终得到所研究对象的结果，发展数学核心素养的同时收获成就感和自信心.值得注意的是，面积公式的推导具有一定的难度，需要教师的提示和辅助.

德育点：从理性维度来说，学生运用由特殊到一般的方法，推理曲线生长前后的数量关系，尝试多角度思考问题，训练严密的思维；从人格维度来说，学生在探究中学会倾听和交流，这是对学生意志力、个性品质等的培养，让学生学会对自己的学习进行审视和反思.

（4）环节4：归纳结论，探源揭秘

师：当n趋于无穷大，即生长无限次时，“雪花曲线”的周长和面积有何性质？

生8：L=

nL，显然极限不存在.

生9：S=

S

-

n

S=S，极限存在.

师（追问）：这个结果说明了什么？

生10：“雪花曲线”的周长是无穷大的，但面积是有限的.

师：通过刚才的研究，我们可以发现：随着“雪花曲线”生长次数的不断增加，其周长不断增加至无穷，而它的面积虽然也在不断增加，但永远不可能超过S.这是一个多么奇妙的现象.“雪花曲线”这个图形，它具有有限的面积，而具有无限的周长. 也就是说，存在一条无限长的曲线，围成了一个有限面积的区域.

师：现在来看，是否存在一种曲线，它的长度可以绕地球好几圈，却能画在一张小小的邮票上？

学生异口同声：是！

师：这种现象最初被人们认为是十分怪异和荒诞的，但随着人们不断探索与研究，逐渐认识到了它的科学价值，并形成了一个新的数学分支——分形几何. 客观自然界中许多事物，具有自相似的结构，局部与整体在形态、功能、信息、时间、空间等方面具有统计意义上的相似性，适当地放大或缩小几何尺寸，整个结构依然不变，比如各国的海岸线、天上的云朵、身上的血管等.

设计意图：通过师生问答、合作讨论，引导学生回顾并解决情境中的问题，教师带领学生对“雪花曲线”从“形”的感性认识，通过“量”的计算过渡，上升到“质”的理性认识，突破本节课的教学重难点.

德育点：从人文维度上来说，一朵小小的雪花蕴含着如此神奇的结论，培养学生辩证唯物思想和动态的数学信念. 学生通过探索发现了事物的本质，揭示了现象背后的真理，感受到了数学学科的实用性和科学性，以此提醒自己用数学的眼光观察世界.

（5）环节5：分形拓展，教学相长

师：下面我们有请几位同学，给大家介绍一下分形几何的相关知识！

A同学介绍分形几何的发展史：