阅读材料指向下高中数学教学的案例研究

［摘  要］ 文章以“等差数列的前n项和”为例，分析如何有效地将阅读材料融入高中数学教学，并谈一谈在阅读材料指向下高中数学教学的思考，以期通过研究为其他阅读材料融入高中数学教学提供启示.

［关键词］ 阅读材料；高中数学教学；案例研究；等差数列的前n项和

[⇩] 引言

阅读材料是教科书的重要组成部分，2019年版高中数学人教A版教材（以下简称“新教材”）设有“阅读与思考”“探究与发现”和“信息技术应用”等阅读材料栏目. 章建跃教授指出：“在高中数学教材中设置‘阅读材料’栏目，为学生提供丰富的具有思想性、实践性、挑战性的，反映数学本质的选学材料，拓展学生的数学活动空间，发展学生‘做数学’‘用数学’的意识.”［1］《普通高中数学课程标准（2017年版2020年修订）》（以下简称《新课标》）指出：“要注重数学文化的渗透，注重信息技术与数学课程的深度融合；要不断引领学生感悟数学的科学价值、应用价值、文化价值和审美价值.”［2］ 这些内容可选择阅读材料作为载体来实现.

但由于阅读材料不是教材正文内容，它常常被师生忽略，导致其教育教学功能未得到充分发挥，而且单独讲授教材中的阅读材料是不可行的，所以考虑将阅读材料融入教学，使得课堂教学更有品质. 那么，如何有效地将阅读材料融入教学呢？邵光华教授指出：“使用新教材时需要特别关注新增内容. 新教材注重数学文化的渗透，在题目背景设置和‘阅读与思考’板块中都有所体现，作为教师应更深入地了解相关历史和背景.”［3］因此，本研究结合新教材中一则新增的阅读材料“中国古代数学家求数列和的方法”，并以“等差数列的前n项和”为例分析上述问题，最后谈一谈阅读材料指向下高中数学教学的思考.

[⇩] “等差数列的前n项和”内容的阅读材料的文本分析

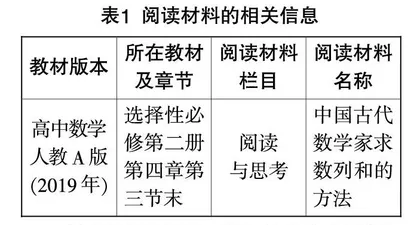
“等差数列的前n项和”内容的阅读材料的相关信息如表1所示：

该阅读材料先对数列求和问题的发展历程进行了简单介绍，然后对刘徽如何发现等差数列求和公式的过程进行了探讨分析，最后在文末讲述了沈括创造的“隙积术”以及分析了杨辉把已知形状、大小的几何图形的求面积、体积的连续量问题转化为求离散量的垛积问题［4］.

等差数列的求和方法“倒序相加法”是历史传承下来的巧妙方法，学生往往觉得它“巧妙”但“想不到”. 而实际上，“倒序相加法”是在深入理解等差数列性质的基础上得到的. 教材编写者为了使教师和学生意识到这一点，在教材中设置了上述阅读材料.

[⇩] 教学案例研究

阅读材料“中国古代数学家求数列和的方法”不仅具有数学教育价值，而且有利于把握数学内容的本质，与《新课标》中的“把握数学本质，启发思考，改进教学”这一理念是相吻合的. 此外，这则阅读材料为教材中的“思考”（即如何避免分类讨论）提供了丰富的数学文化背景（垛积术）. 因此，将这样的阅读材料融入数学课堂教学，可以更好地发挥其探究和德育功能；同时，学生学习数学家的成果有利于理清数学思想方法的由来.基于此，设计如下案例.

（一）教学目标及教学重难点

1. 教学目标

（1）结合古代数学家求数列和的方法，通过猜想到证明，掌握等差数列的前n项和公式及推导方法，并能简单应用.

（2）亲历公式的探索发现过程，体验探索的成功与快乐，渗透特殊到一般、函数与方程、转化等思想，积累基本活动经验，养成严谨的思维习惯，发展数学抽象、逻辑推理与数学运算等数学核心素养.

（3）通过应用等差数列的前n项和公式解决良马和驽马15日所行里数问题，体会“倒序相加法”诞生的曲折过程，感受数学家的探索精神和创新意识.

2. 教学重难点

教学重点：等差数列的前n项和公式.

教学难点：等差数列的前n项和公式的推导.

（二）教学过程

基于上述对阅读材料“中国古代数学家求数列和的方法”的文本分析，以及对教学目标和教学重难点的制定，设计了如下教学流程（如图1所示）：

1. 创设情境，导入新课

【问题情境】

我国魏晋时期的数学家刘徽（图2）在《九章算术》注文中的“盈不足”章给出的第19问是一个等差数列问题：“今有良马与驽马发长安至齐，齐去长安三千里（里是我国市制长度单位，1里=500 m）.良马初日行一百九十三里，日增十三里.驽马初日行九十七里，日减半里. 良马先至齐，复还迎驽马.”

注：原问为“几何日相逢及各行几何？”

【教师活动】

创设情境，设置引导性问题并让学生先计算良马15日所行里数：

（1）记良马15日所行里数为S，请学生列式计算S；

（2）待大部分学生解答完成后，给出刘徽的计算方法为S=193×15+（1+14）××13，学生对比刘徽的计算方法后产生困惑.

【学生活动】

（1）列式计算：

S=193+（193+13）+（193+13×2）+（193+13×3）+…+（193+13×14）=[][15个193]+13×（1+2+3+…+14）=15×193+13×105=4260.

（2）发现1+2+3+…+14与相等，通过计算可验证，但大部分学生对于二者能联系起来是存在困惑的.

设计意图：借助刘徽求等差数列的求和方法创设情境，学生不仅能学到古代数学家求数列和的思想方法，而且通过计算并对比数学家的计算方法后产生困惑，从而激发学生探索知识的兴趣.

2. 探究归纳，初获猜想

南宋的数学家杨辉“善于把已知形状、大小的几何图形的求面积、体积的连续量问题转化为离散量的垛积问题”.例如，求图3“圭垛”中的格点个数总和，杨辉认为虽然圭垛的形状与三角形相似，但要用梯形的面积公式计算，即S==28.

【教师活动】

（1）介绍数学家杨辉的成就并展示“圭垛”图片，结合图形分析的结构，引导学生从“形”的角度理解上述情境中的1+2+3+…+14=（1+14）×.

（2）结合两位数学家的计算方法，引导学生猜想S=1+2+3+…+（n-1）+n=？

【学生活动】

（1）结合梯形面积公式，从“形”的角度进行分析，消除困惑.

（2）通过分析两位数学家的计算方法，将S看成是上底为1，下底为n，高为n的梯形，并结合梯形面积公式猜想得到S=.

设计意图：借助杨辉处理“圭垛”中的格点总数问题完成：①从“形”的角度，帮助学生理解情境中的困惑——1+2+3+…+14=（1+14）×；②为猜想得出S=1+2+3+…+（n-1）+n=奠定基础：引导学生对两个特殊的等差数列求和结果进行分析、比较和归纳，从特殊到一般，猜想出上述一般结果，培养学生合作交流的意识以及合情推理和运算的能力；③为后续借助梯形面积公式的形象记忆等差数列前n项和的两个公式做好铺垫.

3. 演绎推理，证明猜想

问题1：数学讲究严谨，大胆猜想得出的结论还需要细致证明，刚才的猜想正确吗？又该如何证明？

【教师活动】

（1）引导、启发学生用分析法来贯通思路，要证S=，即证2S=n（1+n）（提示：2S可看成2个S相加，n（1+n）可看成n个（1+n）相加），让学生完成证明.

（2）引导学生思考以下两个问题：

①证明过程会用到等差数列的哪条性质？

②证明过程有何特点？（注：教师巡视，观察是否有学生想到将第二个S写成S=n+（n-1）+（n-2）+…+2+1.若没有，教师要对学生的证明过程进行适当引导，让学生感受到“倒序”后的计算简洁、直观.）

【学生活动】

（1）通过独立思考、合作交流、讨论推演，给出证明：

S=1+2+3+…+（n-1）+n①，

S=n+（n-1）+（n-2）+…+2+1②，

①+②：2S=n（1+n）.

所以S=.

（2）思考、交流和讨论：

①等差数列的性质：若｛an｝为等差数列，m+n=p+q（m，n，p，q∈N*），则a+a=a+a.

②发现证明过程的巧妙之处，提炼出“倒序相加法”的操作技能和思想.

设计意图：结合阅读材料和教科书提出一个可能发现“倒序相加法”的思想：①使学生认识到研究问题的一般思路为“探索—归纳—猜想—证明”；②在“2S可看成2个S相加，n（1+n）可看成n个（1+n）相加”这样的启发下，想到用“倒序相加法”求1+2+3+…+（n-1）+n，展现了数学发现中的“触类旁通”“灵感”等要素，为学生分析问题和解决问题做出示范［5］；③为“倒序相加法”推广到一般的等差数列求和埋下了伏笔，同时揭示了该方法的根源所在——等差数列的性质，让学生认识到定义、性质的重要性，这是一切数学推理的源泉，同时培养学生演绎推理的能力；④讲解1+2+3+…+（n-1）+n是为了得出等差数列前n项和“公式2”的另一种推导方法，让学生意识到所有的等差数列求和问题都可以转化为求1+2+3+…+（n-1）+n.

4. 方法推广，获得公式

问题2：能将上述方法推广到“求首项为a，公差为d的等差数列｛a｝的前n项和S”吗？

问题3：若将通项公式a=a+（n-1）d代入“公式1”，又能得出什么表达式呢？

【教师活动】

（1）对学生的推导过程进行完善、板演，并总结.

（2）引导学生将a=a+（n-1）d代入“公式1”得出“公式2”：S=na+d.

【学生活动】

（1）通过小组合作交流，完成推导：

S=a+a+a+…+a+a①，

S=a+a+a+…+a+a②，

①+②：2S=n（a+a）.

所以S=.

得到等差数列｛a｝的前n项和“公式1”：S=.

（2）将a=a+（n-1）d代入“公式1”得出“公式2”：S=na+d.

设计意图：将“倒序相加法”推广至一般的等差数列求和问题中，体现特殊到一般的数学思想方法，使得等差数列｛a｝的前n项和公式的推导比较自然，也符合学生的认知规律，发展学生的逻辑推理核心素养；将“公式1”变形得到“公式2”，有助于学生在后续的学习中正确选择公式.

5. 公式剖析，外化于形

结合数学家杨辉求“圭垛”中格点个数的方式（借助梯形面积公式），分析等差数列的前项和公式的结构.

公式1：S=

公式2：S=na+d

设计意图：通过阅读杨辉借助梯形面积公式计算“圭垛”格点总数问题，获得一般启示：借助梯形面积公式，帮助学生形象记忆等差数列求和公式，渗透数形结合思想方法，发展学生的直观想象核心素养.

6. 公式应用，传道解惑

问题4：回到刚才的情境中，

（1）现在同学们知道数学家刘徽是如何计算的吗？用的是哪个等差数列求和公式，请指出相应的基本量. （注：S=193×15+（1+14）××13）

（2）请同学们利用等差数列求和公式计算出S.

问题5：结合情境中计算S的过程，请同学们思考“如果不从‘公式1’出发，你能用其他方法得到‘公式2’吗？”

【教师活动】

（1）引导学生用等差数列求和公式解决问题4和问题5.

（2）结合刘徽计算的过程提示学生将S=a+a+a+…+a+a化为S=a+（a+d）+（a+2d）+…+［a+（n-2）d］+［a+（n-1）d］，进而化为S=na+［1+2+3+…+（n-1）］d进行思考分析.