把握关键节点，实现数感衔接

摘 要：数感是一种感觉，这种“感觉”不仅需要经过长期的训练，通过感受和领悟逐渐变成自身具有的能力，更要把握好学习的关键节点，从而实现数感发展从“确定”到“不确定”、从“真实”到“虚拟”、从“绝对”到“相对”的衔接，形成“数”认识的完整体系，逐步解析数的内涵，完善数的意义，拓展数的领域。

关键词：小学数学；数感；“种子课”

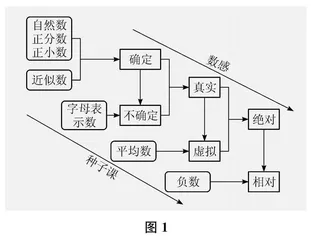
随着《义务教育数学课程标准（2022年版）》（以下简称“课标”）的颁布，核心素养表现中的“数感”再一次成为小学数学界的讨论重点。数感是一种感觉，这种“感觉”不仅需要经过长期的训练，通过感受和领悟逐渐变成自身具有的能力，更要把握好学习的关键节点。梳理小学数学中数概念的相关内容（如图1所示）后，笔者以为，数感发展有三个关键节点——确定到不确定、真实到虚拟、绝对到相对，需要做好衔接工作。

一、解析数的内涵，实现“确定”到“不确定”的衔接

小学阶段有关数的认识是从自然数开始的。在低年段时，学生通过对1个苹果、2张桌子等这样的数量的抽象得到自然数1—9，又通过数小棒、正方体等产生更大的自然数。这些自然数都是描述确定的具体数量。此外，学生也经常遇到4个苹果是1个苹果几倍的问题，这是对数量关系的抽象，“4倍”依然是描述一个具体的、确定的数量关系。由此可见，自然数在表示数量和数量关系时指向的都是确定的量。那么，正分数、正小数是不是也像自然数一样呢？确实是一致的，它们实际上是自然数的拓展，当然也就表示一个具体的、确定的数量或数量关系，只是它们用来表示比计数单位“1”更小的数量。因此，这一阶段学生的数感习得，可能都停留于“确定的、具体的”，都是一一对应的点对点关系。

而到了四年级认识近似数时，数描述的不仅是一个点，而是拓展到一个范围。数感由原来的一个点向一条线或一个面进阶，因此，我们不妨把这部分内容作为“种子课”，它是数内涵的进一步深化。在教学时，教师要在具体的数和一个范围的数之间搭起一座桥梁，让学生对数的理解更全面、更立体。不过，此时的数依然是确定的，只是变成了一个取值范围。

而数感从确定到不确定转变的重要节点在《字母表示数》一课，此时的数具有了不确定性——它存在“未知”的特点，是一个会根据相应的信息而变化的量，或因情境信息的不同确立不同的量与量之间的数量关系。在此课的学习中，有些教师会侧重“怎么用字母表示数”，这是不够的。如果要实现学生的数感从确定到不确定的顺利衔接，“字母表示不确定的数”“字母表示量与量的数量关系”“为什么要用字母表示数”等问题都是值得被关注的。从一个数表示具体的数量或数量关系，到一个字母或含有字母的式子表示一个数量或数量关系，学生是存在一定的理解障碍或疑惑的。因此，《字母表示数》一课教学，我们需要抓住“关系”做文章，让学生体验到字母虽然是不确定的，但也是“确定”的——它们能概括一组关系，通过它就能发展数量的特征与关系。这也就是数学的简洁性的重要体现，同样也真正完善了对数感不确定性的诠释。

由此，有关数的内涵，我们在这一阶段需要完成从确定到不确定的过渡和衔接（如图2所示），让学生从确定的数量和数量关系发展到不确定的变量，形成一个较为完善的数感体系。

二、完善数的意义，实现“真实”到“虚拟”的衔接

课标特别把“百分数的认识”这部分内容划归至统计与概率学习领域，这意味着从统计的视角认识数也十分必要。而《平均数》一课是把数与统计量关联起来的“种子课”，也就是要让学生领悟到平均数是一个虚拟数，而前面学习的自然数、正分数、正小数、近似数等都是真实的数。那么，如何从真实的数过渡到虚拟的数便成为第二个关键节点。因此，在教学《平均数》一课时，我们需要让学生从现实生活中收集数据、分析数据，进而体验数据的变化和奥秘。

例如，教师设计了“记数大王”游戏作为课堂导入环节，带领学生感受数据的变化，体验数产生的真实性。而平均数却有可能不在这些现实数据中，它是“匀”出来的，所以具有虚拟性；它不仅受最大值和最小值的影响，还可能因为数据的差异性而使得它与其他数据“格格不入”。玩了5次后，其平均数是6，那么第6次的数据也将影响这6次的平均数。因此，无论是用移多补少、取长补短，还是先合后分，其本质是一致的，都是把原有的数进行均分，从而“匀”出一个数，用来描述具有代表性的一般水平，是为了满足统计和分析问题需要。

当然，这种虚拟性并不是凭空捏造的，而是依据数据的特征，分析数据的关联，根据现实需求，找到一个合适的“数”来代表一组数量的水平。它可能在这组数中，也可能不在这组数中；可能是整数，也可能是小数。其实，要让学生完成从原来真实的数到虚拟的数的转变并非易事，学生会有这样的疑问：数应该是确定的，为什么在这里又变成虚拟的了？是的，如果作为统计量那应该就是变化的、虚拟的。玩5次的平均数是6，那下一次能确定一定是6吗？显然是不能确定的，这就需要教师在教学设计中创建任务让学生去体验，他们才能真正地理解。此外，平均数是针对一组统计量的，它应该是对整体数据的描述，不是点对点的，也不是点对面的，那么这样的数可能就不是真实存在的，它是需要虚拟得到的。

三、拓展数的领域，实现“绝对”到“相对”的衔接

无论是自然数、正分数、正小数、近似数、字母表示的数，还是平均数，这些数都具有绝对性。这些数为什么是绝对的呢？因为它们都是表示具体的数量的多与少，或者描述一个量的整体情况，并未反映出数相对性的一面。只有《负数》一课的出现，才真正地让学生体验到数的相对性——正与负是相对的，描述的是一种“状态”。因此，《负数》一课就是实现从绝对到相对衔接的“种子课”。当然，负数的产生具有必然性，它是拓展数概念域的需要。由正到负，不仅能拓宽学生对数概念的认知范围，还能让学生体会相对、相反的现象，以及事物的两种不同的状态。因此，本课教学一般从生活中的温度等模型切入，让学生基于生活中的冷热现象等领会到“相对性”，从而抽象出“正数”与“负数”这一数学模型。当学生从具体描述多少的数，走向表示相对状态的数，这一跨越便融通了学生对数的固有认识：数只能表示数量的多少。从正到负，也满足了学生对现实生活的表达，现实生活中不仅有“黑”，也有“白”。课标提出，要会用数学的眼光观察现实世界、会用数学的思维思考现实世界、会用数学的语言表达现实世界，那么，负数的产生就是对现实世界的表达，同样促进了学生用数学的眼光审视现实世界，从而有关数的相对性表述的必要性便一览无遗。所以，这是学生建立完整的数感体系的一个重要支点。

由此，负数是小学阶段认识数的一个重要分水岭，无论是链接初中的数轴与绝对值等知识，还是体现其在生活中的广泛运用，都有举足轻重的作用。它是学生建立完整的数概念的重要组成部分，也是学生数感结构化、整体化和关联化的重要支撑。

从确定到不确定，从真实到虚拟，从绝对到相对，不断地拓展数的内涵、意义和领域，学生数感的发展也就能循序渐进，一步一个脚印，从孤立的点，发展成线、面，再到立体的结构。这便是课标中最为突出的要求，即结构化的内容，促进结构化的思维的生成，推动结构化的数感的形成。上好“种子课”，把握数感发展的关键节点，让学生的素养发展真正落地。